波動② ドップラー効果

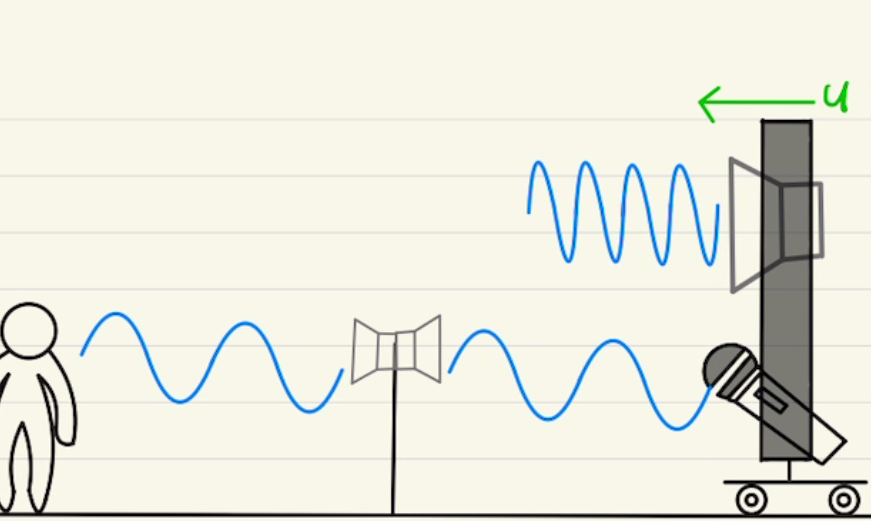
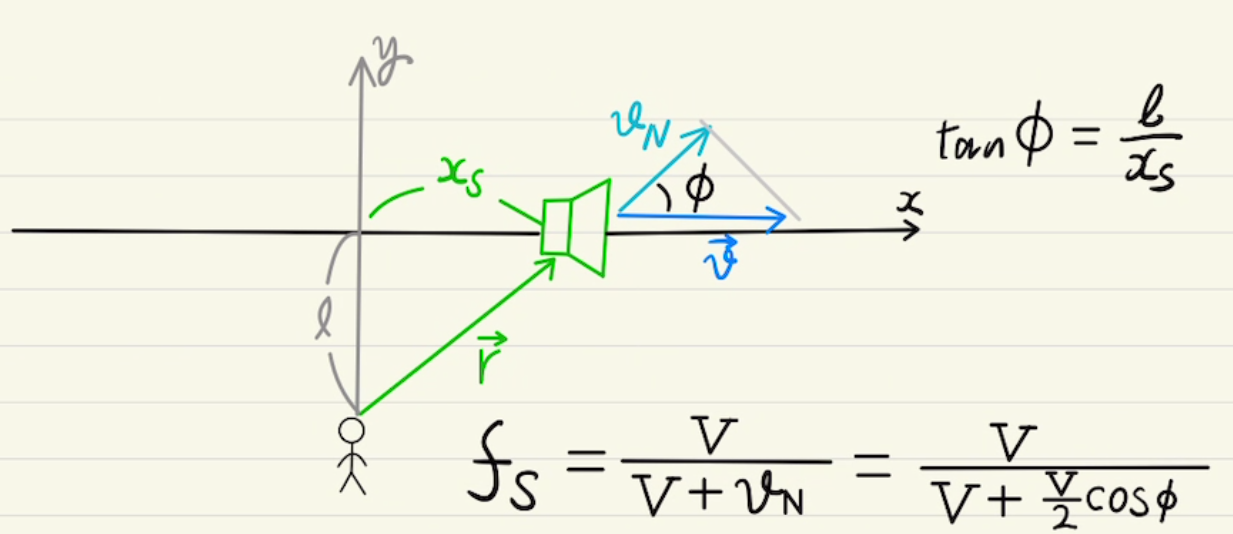
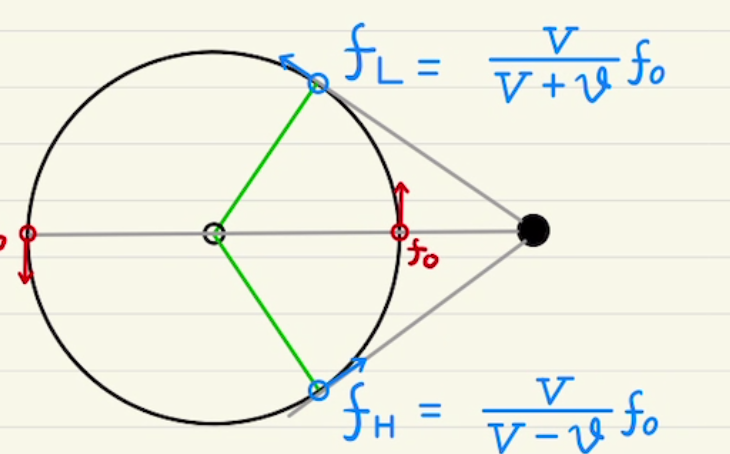
救急車が近づいている場合音が高くなり、遠ざかっていくと音が低くなっていくのは聞いたことがあると思います。
そのドップラー効果とその反射によって生まれる音のうなりについて数式を用いて考えていきます。

ドップラー効果

まず押さえておかないといけないのは音は空気を媒介しているため、動いている物体から音が出ても音の速度が変わらないということです。
その速度を$V$とします。

・音源が動く場合
スピーカーが速度$v_s$でマイクに近づいているとします。

最初にスピーカーから音を出したとき$t=0$として、マイクから距離$Vt_0$だけ離れていたとすると、$t_0$秒後に音はマイクに届きます。このとき、$t=t_0$となります。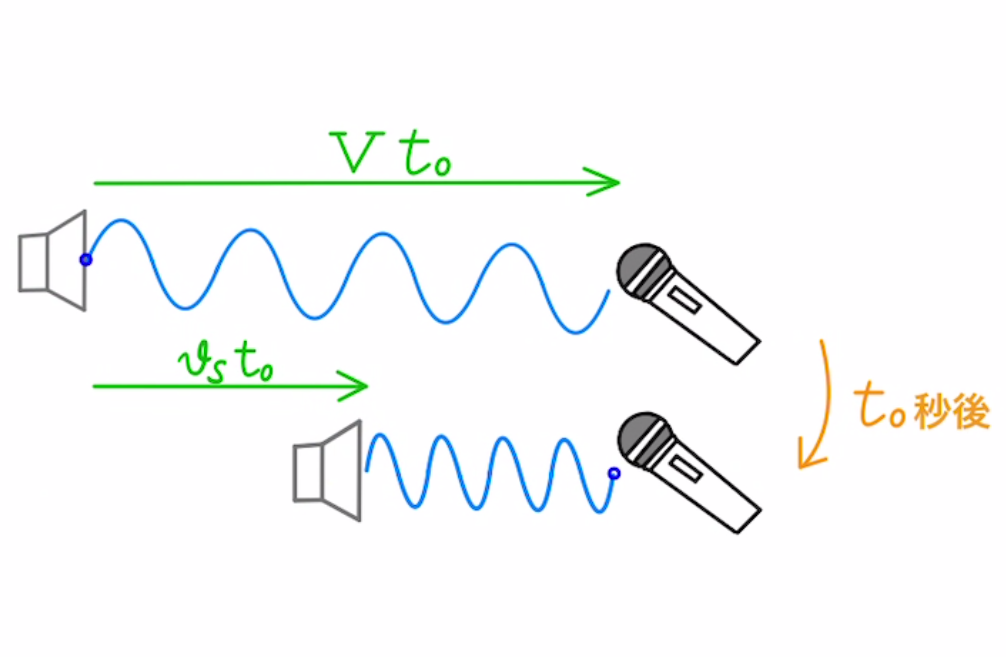

$t=t_0$のときスピーカーとマイクの距離は$(V-v_s)t_0$となります。
よって$t=t_0$のときに発された音は $t_1=\frac{(V-v_s)t_0}{V}$秒後に届き、静止しているときより早く音が届くことになります。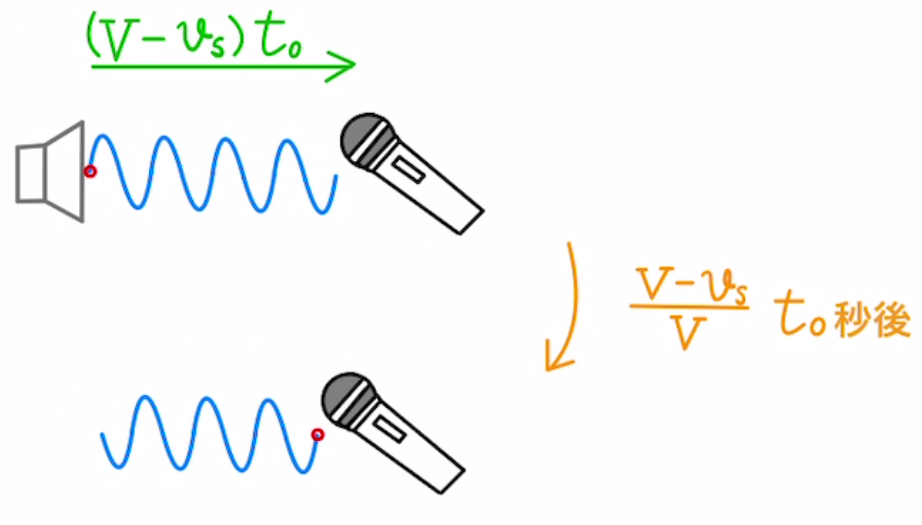

これは言い換えればスピーカー上では$t_0$秒間鳴らしている音を、マイクは$t_1$秒$(<t_0)$の間しか聞こえないことになります。
しかし、スピーカーが静止してても動いてても $t_0$秒間に出す音の数は一緒であり、波の数($f_0t_0$)は静止しているときと変わりません。

つまり、 $\frac{t_0}{t_1}$倍だけ音が早くなる=音が高くなるので、(音を早回ししているように聞こえます。)
$f_s = \frac{V}{V-v_s}f_0$

・聞く側が動く場合
スピーカーは静止しており、速度$v_m$でマイクが遠ざかっているとします。

マイクに音が届いたときに距離$(V-v_m)t_0$だけ離れていたとすると、$ \frac{V-v_m}{V}t_0 $秒前にスピーカーから出した音をマイクは拾ったことになります。

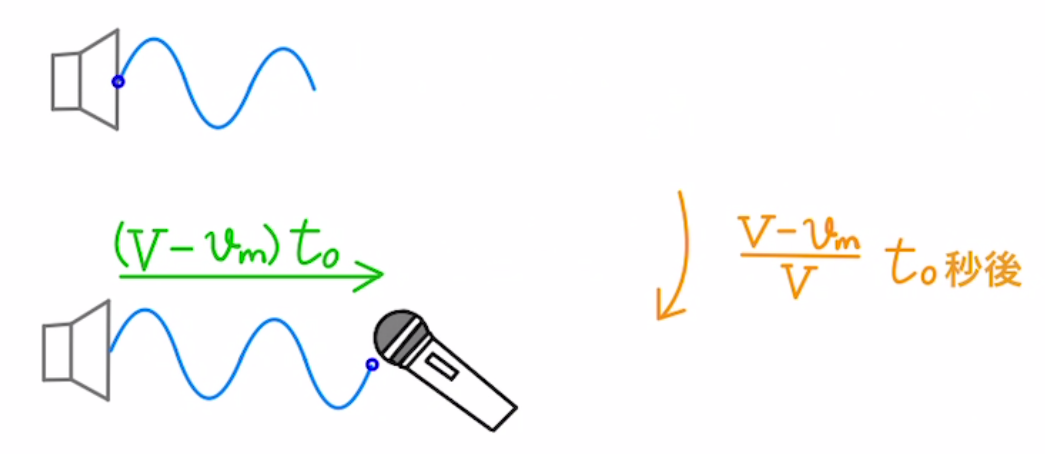
このときにスピーカーから出た音は$t_0$秒後にマイクが拾います。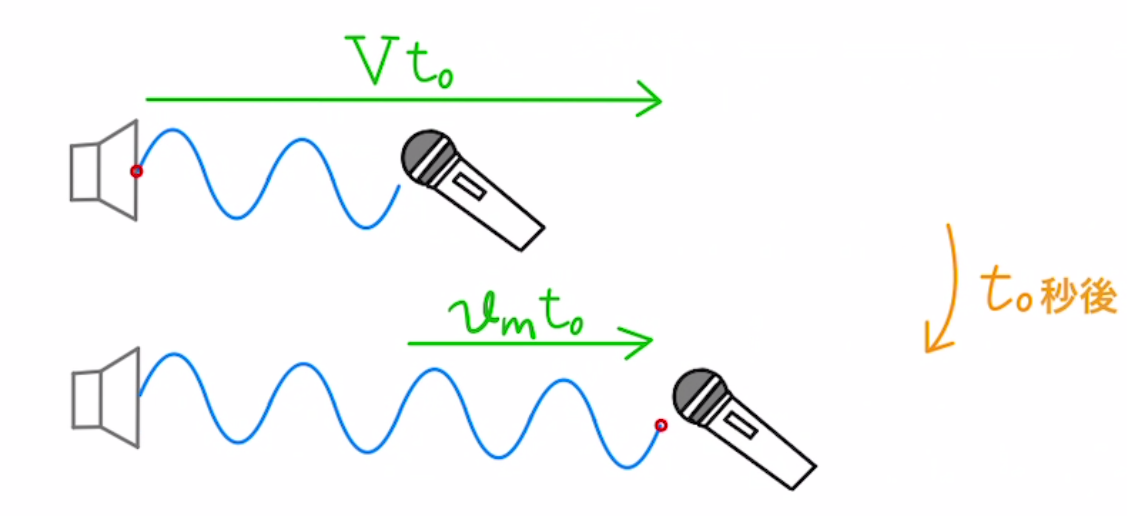

よってスピーカーでは $(V-v_m)t_0$秒間鳴っていた音が、マイクでは$t_0$秒間聞こえることになります。
つまり、 $\frac{ V-v_m }{V}$倍だけ音が遅くなる=音が低くなるので、(音を早回ししているように聞こえます。)
$f_m = \frac{V-v_m}{V}f_0$

これらを組み合わせることによって
$$f_d = \frac{V-v_m}{V-v_s}f_0$$
が成り立ちます。

うなり

少しだけ周波数が違う音を鳴らすと、音がうなっているように聞こえます。

この原理について数式で考えてみたいと思います。

周波数$f=\frac{1}{T}$であることを踏まえると二つの波の式は
$ y_1( {\color{orange} t} , {\color{green} x}) = A\sin{2π(f_1 {\color{orange} t} – \frac{ {\color{green} x} }{λ_1})}$
$ y_2( {\color{orange} t} , {\color{green} x}) = A\sin{2π(f_2 {\color{orange} t} – \frac{ {\color{green} x} }{λ_2})}$
と書けるため、この二つの波の重ね合わせは
$y ( {\color{orange} t} , {\color{green} x}) =y_1+y_2= 2A\cos{π((f_1-f_2) {\color{orange} t} + (\frac{1}{λ_1} + \frac{1}{λ_2} ) {\color{green} x} )} ・ \sin{π((f_1+f_2) {\color{orange} t} + (\frac{1}{λ_1} – \frac{1}{λ_2} ) {\color{green} x} )} $
となります。

すこしわかりづらいので$x=0$のときを例に考えてみましょう。
波の式は
$y ( {\color{orange} t} , {\color{green} 0}) = 2A\cos{π(f_1-f_2) {\color{orange} t} } ・ \sin{π(f_1+f_2) {\color{orange} t}} $
となります。
これは二つの波の掛け算であり、
$ D ( {\color{orange} t}) = 2A\cos{π(f_1-f_2) {\color{orange} t} } $
とすれば、
$y ( {\color{orange} t} , {\color{green} 0}) = D ( {\color{orange} t}) \sin{π(f_1+f_2) {\color{orange} t}} $
となります。
$ D ( {\color{orange} t}) $の波を書くと下のような波になります。

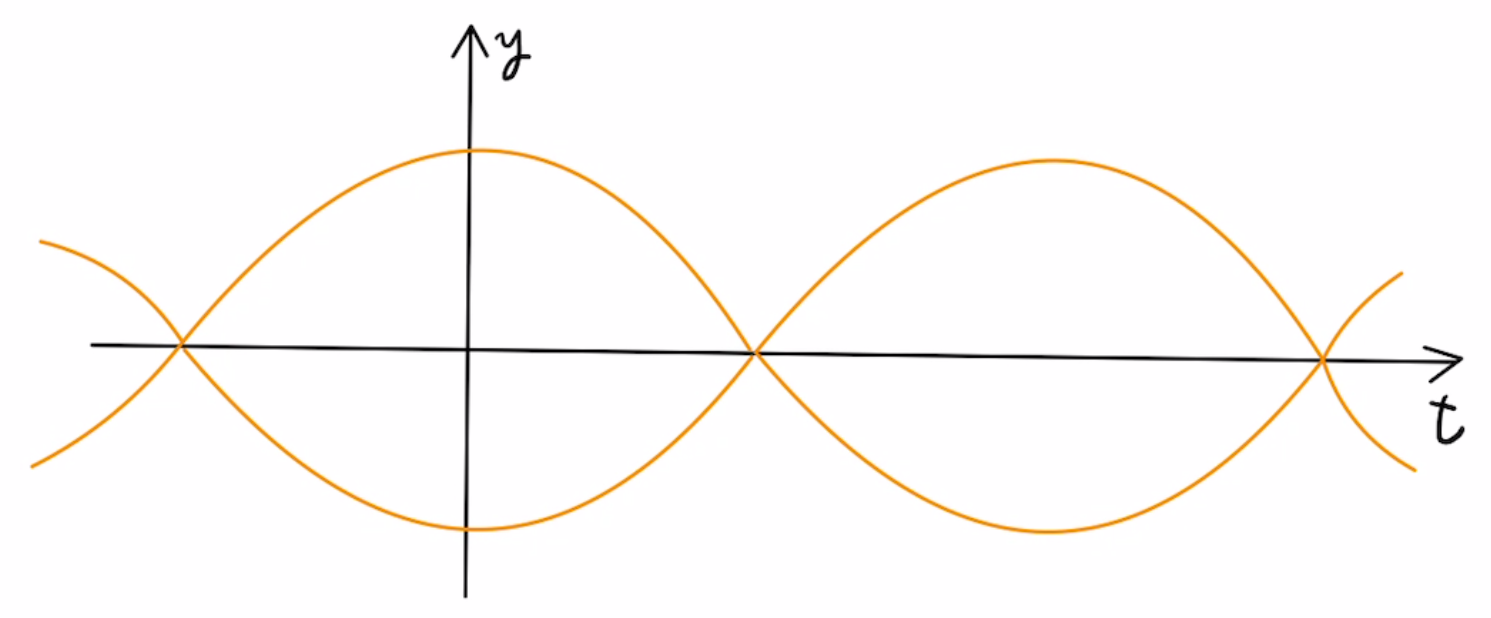
このことから波の重ね合わせの式
$ y ( {\color{orange} t} , {\color{green} 0}) = D ( {\color{orange} t}) \sin{π(f_1+f_2) {\color{orange} t}} $
のグラフは下の図の青色の部分となります。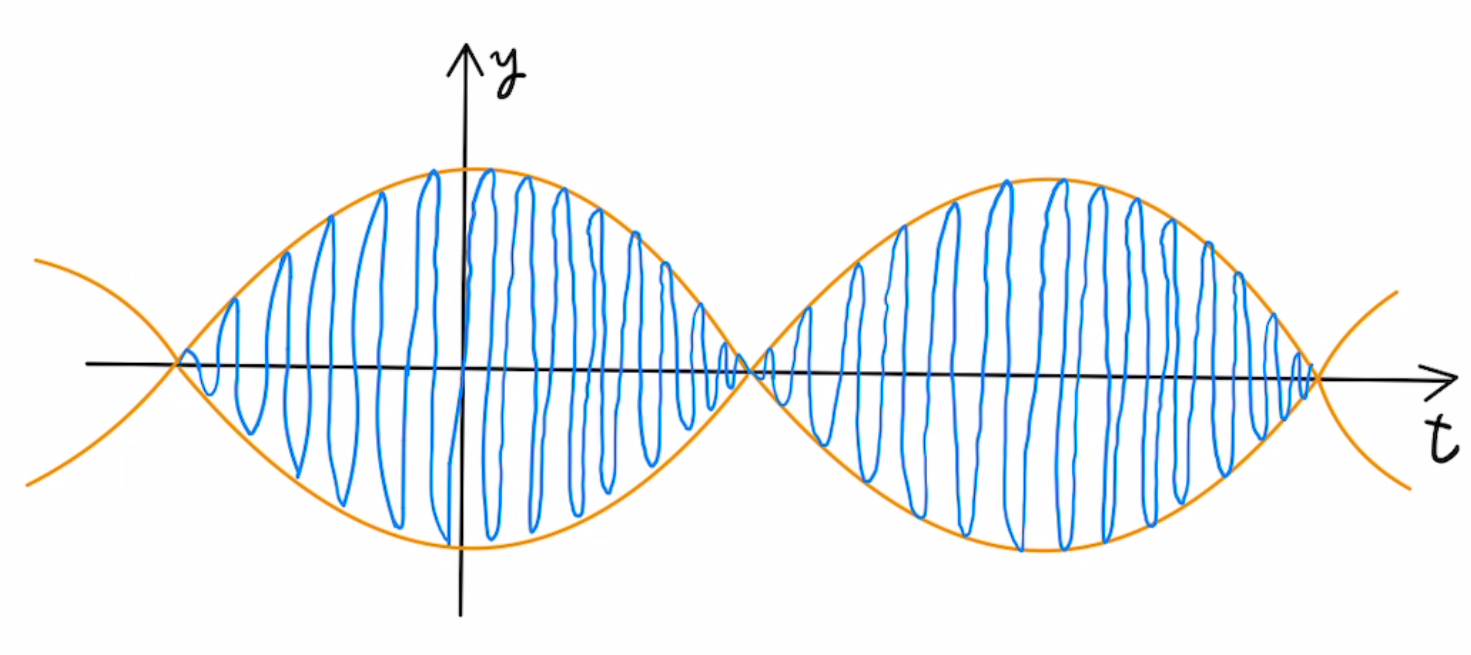

この $ D ( {\color{orange} t}) $ の部分がうなりの正体であり、周波数$f_B=|f_1-f_2|$となります。

ここでは$x=0$を例にとりましたが、他の点でも位相が少しずれるだけで基本的な構造は変わりません。