ケプラーの第1法則 導出
大学受験では導出を無理にやる必要はないですが、一応記しておきます。
ここでは極座標というものを使います。
今まで座標を$x,y$で表していた座標を、原点からの距離$r$と$x$軸からの角度$θ$で表します。
つまり、
$$ \begin{bmatrix} x \\ y \end{bmatrix} = r\begin{bmatrix} \cos{θ} \\ \sin{θ} \end{bmatrix} $$
となります。\dot{θ}
$r$も$θ$も時間で変化する、つまり時間の関数であることに留意する。
これを二回時間微分すると加速度が求められ、
$$ \begin{bmatrix} a_x \\ a_y \end{bmatrix} = (\ddot{r}-2r \dot{θ}^2 ) \begin{bmatrix} \cos{ θ } \\ \sin{ θ } \end{bmatrix} + (r\ddot{θ}+2\dot{r} \dot{θ} ) \begin{bmatrix} -\sin{ θ } \\ \cos{ θ } \end{bmatrix} $$
となります。
これは$\vec{r}$平行方向である $ \begin{bmatrix} \cos{ θ } \\ \sin{ θ } \end{bmatrix} $ と、 $\vec{r}$垂直方向である$ end{bmatrix} + (r\ddot{θ}+2\dot{r} \dot{θ} ) \begin{bmatrix} -\sin{ θ } \\ \cos{ θ } \end{bmatrix} $に書き直せます。
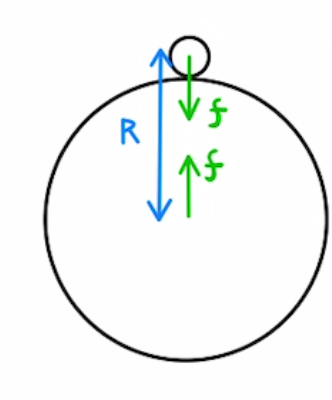
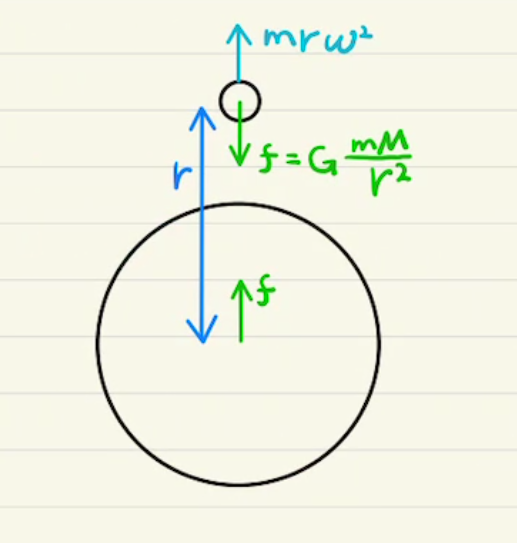
つまり$m\vec{a}=\vec{f}$は
$m (\ddot{r}-2r \dot{θ}^2 ) = -G\frac{mM}{r^2} $ ①
$m (r\ddot{θ}+2\dot{r} \dot{θ} ) = 0 $ ②
の二式に書き直せます。
式②から $r(r\ddot{θ}+2\dot{r} \dot{θ}) = 0$
$⇒ \frac{d}{dt}(r^2 \dot{θ}) = 0$
$⇒ r^2 \dot{θ} =一定$
となります。
これは面積速度一定の式の極座標表記に相当します。
つまり、 $\frac{1}{2} r^2 \dot{θ} = \dot{S}$となります。
$\dot{θ} = \frac{2 \dot{S} }{r^2} $
なので、
$\frac{dr}{dt} = \frac{dr}{dθ}\frac{dθ}{dt} = \frac{dr}{dθ} \frac{ 2 \dot{S} }{ r^2 } $
さらに時間で微分して
$\ddot{r} = 4\dot{S}^2\frac{ 1}{ r^2 } \frac{ d}{ dθ } ( \frac{ 1}{ r^2 } \frac{dr}{ dθ } ) $
これを①に代入すると、
$ 4\dot{S}^2\frac{ 1}{ r^2 } \frac{ d}{ dθ } ( \frac{ 1}{ r^2 } \frac{dr}{ dθ } ) -r(\frac{2\dot{S}}{r^2})^2 = -G\frac{M}{r^2} $
ここで$p=\frac{1}{r}$とすると、
$4\dot{S}^2p^2\frac{ d}{ dθ } ( p^2 \frac{dr}{ dθ } ) -\frac{1}{p}(2\dot{S}p^2)^2 = -GMp^2$
ここで $\frac{dr}{ dθ } = \frac{d(p^{-1})}{ dθ } = -\frac{1}{p^2}\frac{dp}{ dθ } $から
$4\dot{S}^2p^2\frac{ d}{ dθ } ( – \frac{dp}{ dθ } ) -\frac{1}{p}(2\dot{S}p^2)^2 = -GMp^2$
これを計算すると
$ \frac{ d^2p}{ dθ^2 } = -(p – \frac{GM}{2\dot{S}})$
さらに、P= p – \frac{GM}{2\dot{S}}とすると
$ \frac{ d^2P}{ dθ^2 } = -P$
この微分方程式は単振動のものと同等であり、これを解くと
$P=C_1\cos{θ}+ C_2\sin{θ} $
で $ C_1,C_2$は初期位置、初速度で定まる定数。
今回はわかりやすさのために初期位置を$P=0$となるように座標設定をします。
このとき、
$p=C_1\cos{θ} + \frac{GM}{2\dot{S}} $
$⇒r= \frac{ \frac{ 2\dot{S} }{ GM } }{ 1+ \frac{ 2\dot{S}C_1 }{ GM } \cos{θ} } $
これは二次曲線の式になります。
このとき離心率$ε= \frac{ 2\dot{S}C_1 }{ GM } $となります。
$ 0<ε<1 $の時楕円運動となります。
一方で $ ε=1 $だと放物線、 $ 1<ε $では双曲線となり、一回だけ接近して以降はなれていく彗星の軌道にもなりうることがわかります。