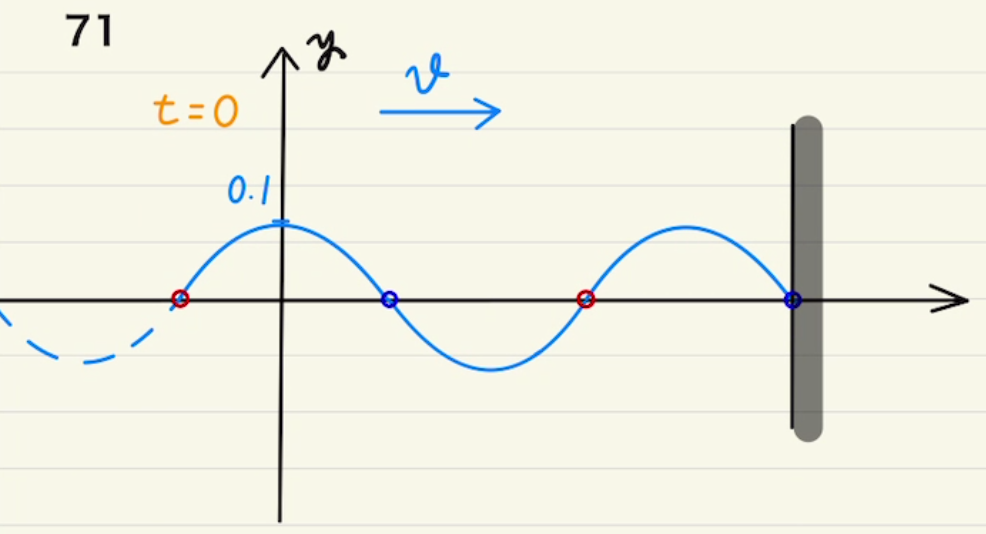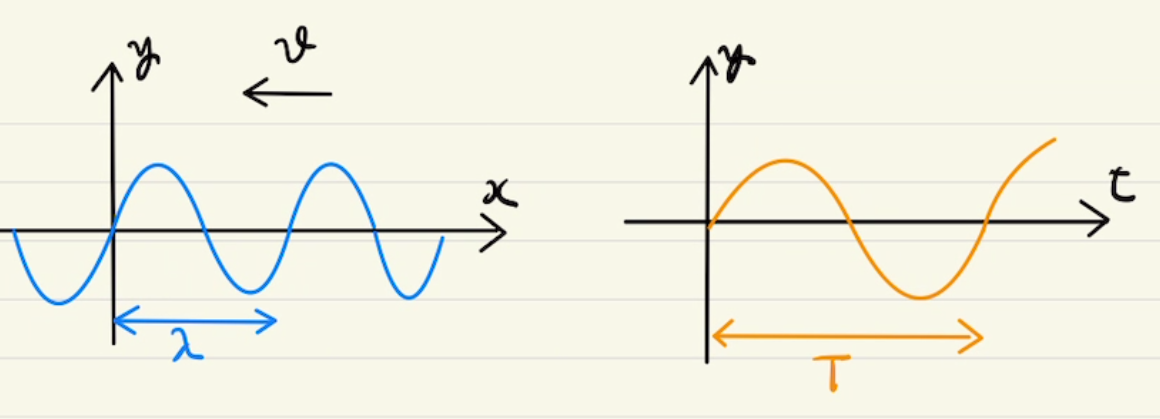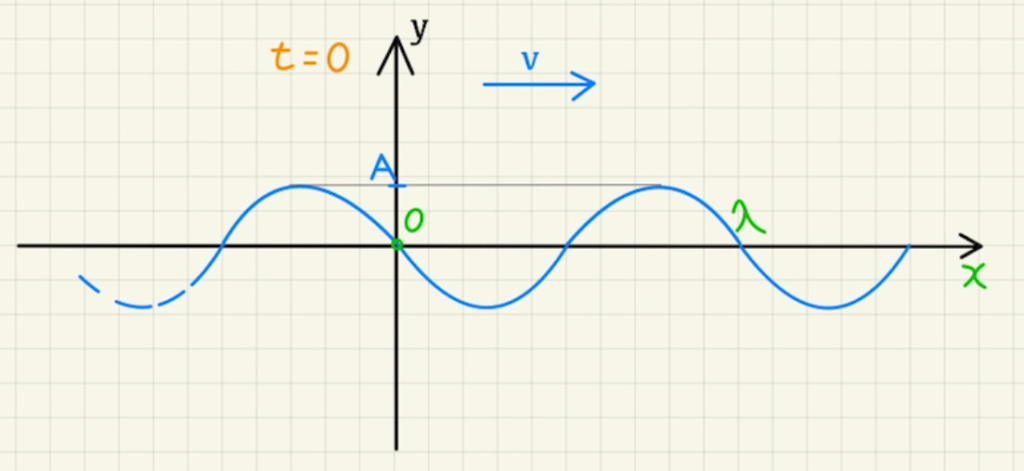
図のようなsin波が右に向かって速度$v$で動いているとします。
これの波の高さ$y$は時刻$ {\color{orange} t},$ 位置${\color{green} x} $の二つによって定まります。(3秒後に1m先では波の高さはいくつだ、といったように求められる。)
つまり、 二変数関数$y( {\color{orange} t} , {\color{green} x} )$を知ることができれば、波の全貌を知ることができるということです。
上の$y-x$グラフをすこしずつ右に移動していくことを考えます。
このとき、$x=0$に注目すると、少しずつ値が大きくなっているのがわかります。
$x=0$での波が時間が進むにつれ、どのような変化になるかをプロットしていくと右側の図のようになります。
$y-t$グラフとなります。
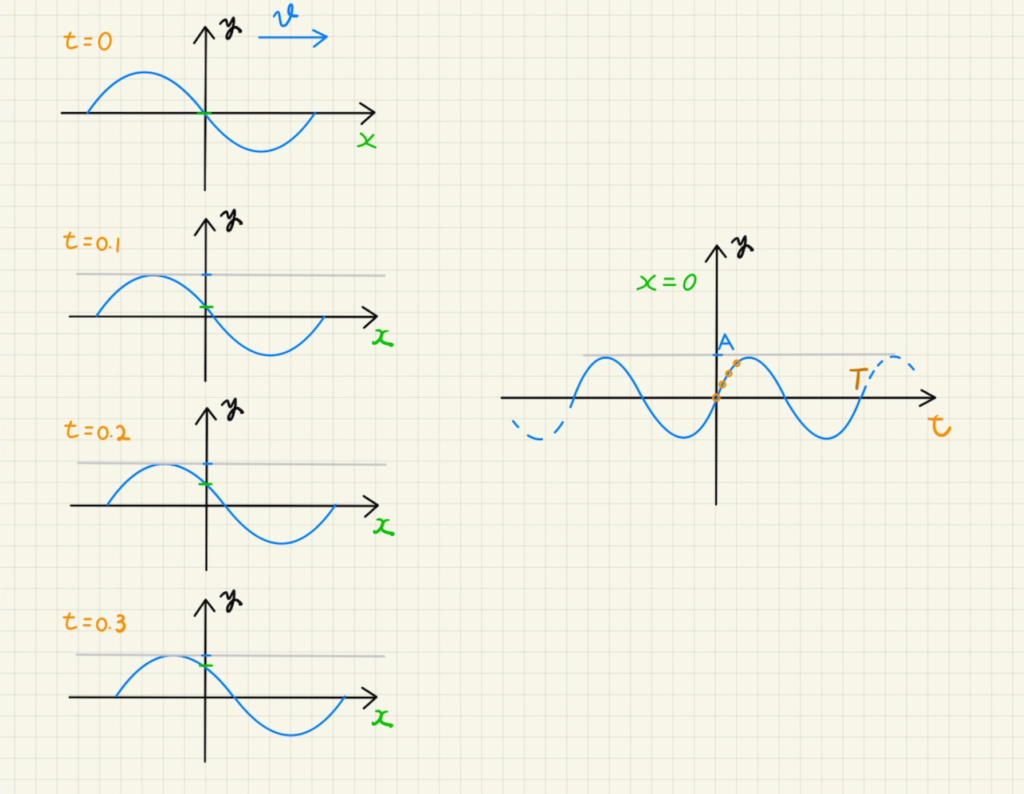
周期を$T$として位置$x=0$での時間変化を式にすると
$y( {\color{orange} t} , {\color{green} 0} ) = A\sin{2π(\frac{ {\color{orange} t} }{T})}$
となります。
位置が$x$のときとのズレを考えましょう。
速度$v$で進んでいるわけですから、$x=x$の波は$\frac{x}{v}$秒前に $x=0$を通っています。
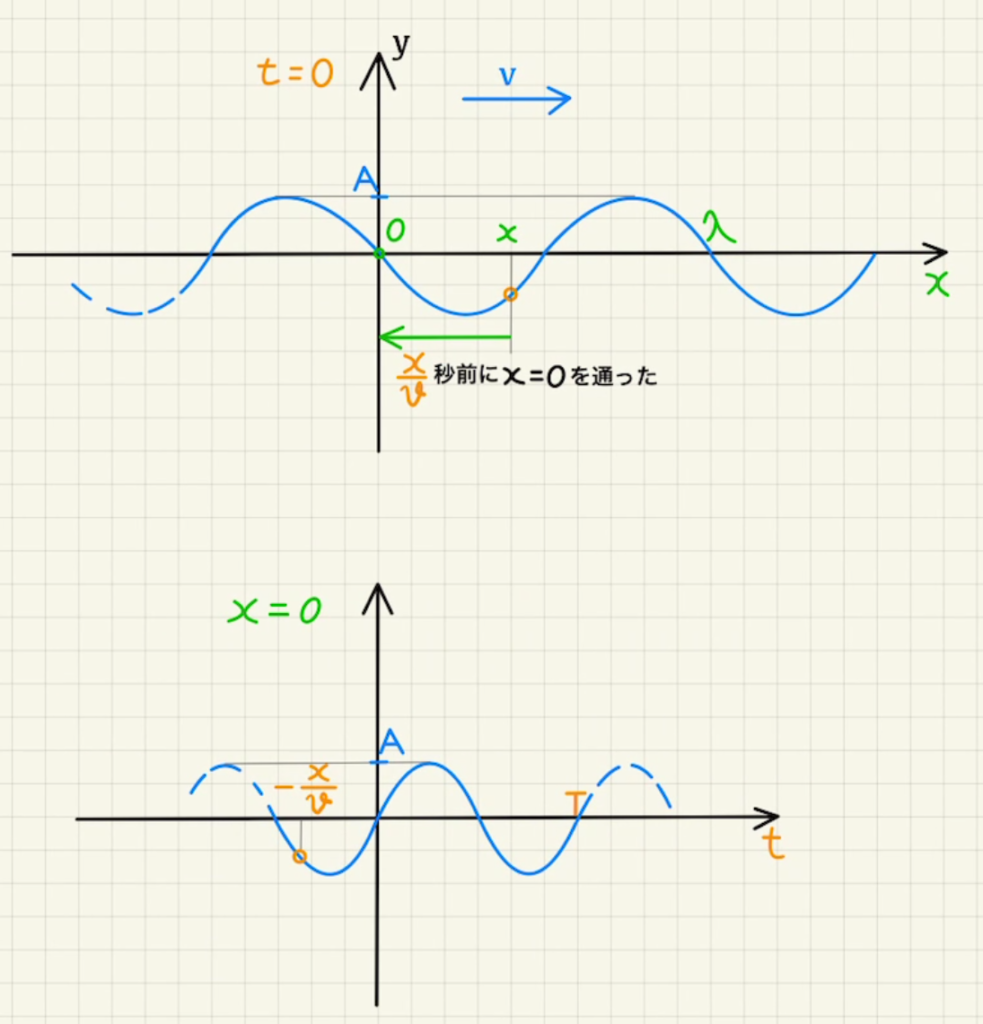
$ y(t,x) = y(t- \frac{x}{v},0) = A\sin{2π(\frac{(t-\frac{x}{v})}{T})}= A\sin{2π(\frac{t}{T} – \frac{x}{vT})} $
となり、波長$λ=vT$なので、波の式は下のようになります。
$$ y( {\color{orange} t} , {\color{green} x}) = A\sin{\left(2π(\frac{ {\color{orange} t} }{T} – \frac{ {\color{green} x} }{λ})\right)}$$
これが波の基本の式になります。
また、$ \sin $の中身$ 2π(\frac{ {\color{orange} t} }{T} – \frac{ {\color{green} x} }{λ} ) $を位相といいます。
補足
波の式はどの位置で$x=0$になるか、どの時刻で$t=0$になるかでスタート地点が$y=0$にならない場合があります。
そのため、波の式をより一般化すると、
$$ y( {\color{orange} t} , {\color{green} x}) = A\sin{\left(2π(\frac{ {\color{orange} t} }{T} – \frac{ {\color{green} x} }{λ}) + θ_0\right)}$$
となり、$θ_0$を初期位相と言います。
$θ_0=0$のとき$\sin$の式になり、 $θ_0=\frac{π}{2}$のとき$\cos$の式になります。
さらに、 $θ_0=π$のとき$-\sin$の式になり、 $θ_0=\frac{3π}{2}$のとき$-\cos$の式になります。
そのため、 $ \sin,\cos$は本質的には変わらないと考えてよいです。
自由端と固定端
・自由端反射
端が上下方向に自由に動く状態での波です。
このとき、端に入った波はそのまま返ってきます。

つまり、反射波のイメージとしては、端よりLだけ右から左向きに入射波と同じ波が出されているのと同じと考えてください。
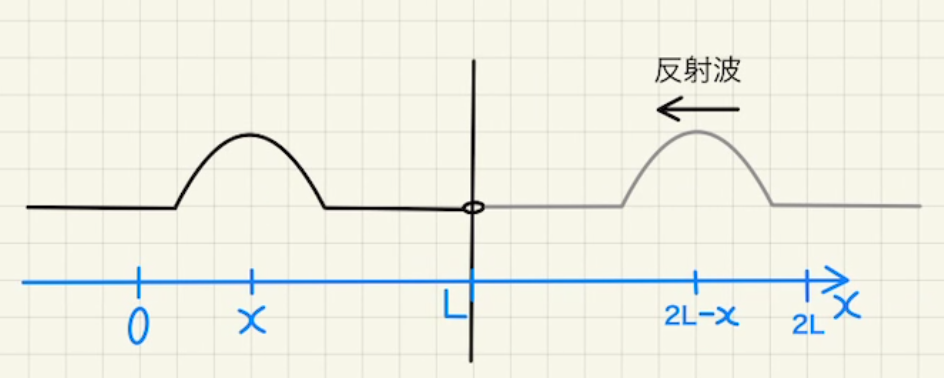
反射波$ y_r $は以下のように表せます。
$$ y_r( {\color{orange} t} , {\color{green} x}) = A\sin{\left(2π(\frac{ {\color{orange} t} }{T} – \frac{2L- {\color{green} x} }{λ})\right)} $$
・固定端反射
固定はの場合は反対方向になって返ってきます。
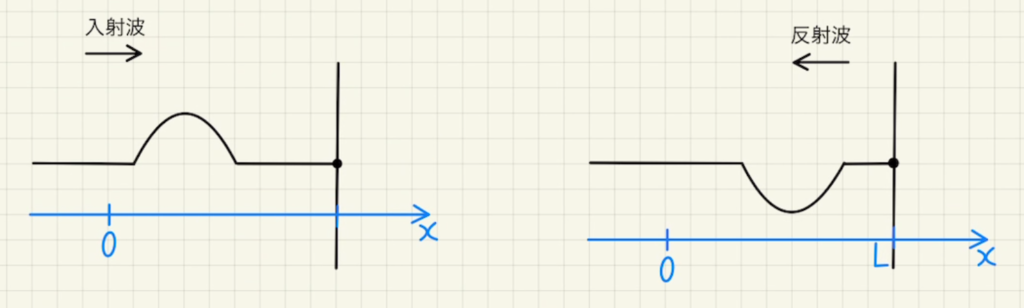
つまり、反射波のイメージとしては、端よりLだけ右から左向きに反射はと逆の波が出されているのと同じと考えてください。
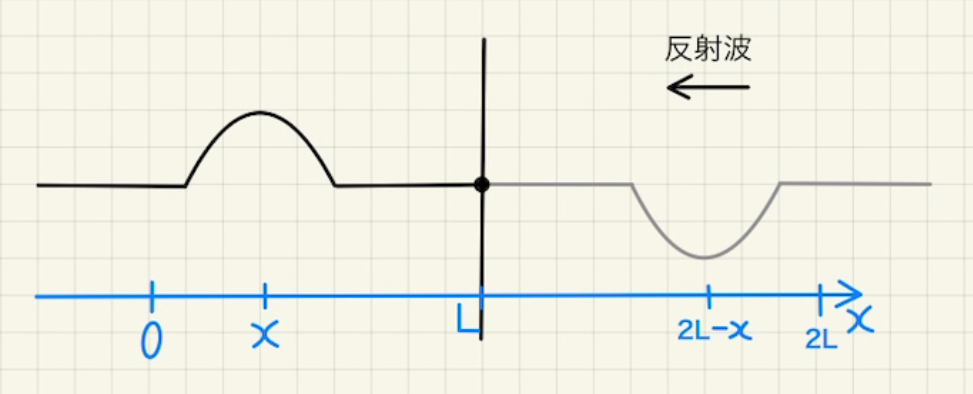
反射波$ y_r $は以下のように表せます。
$$ y_r( {\color{orange} t} , {\color{green} x}) = -A\sin{2π(\frac{ {\color{orange} t} }{T} – \frac{2L- {\color{green} x} }{λ})} $$
反射波の合成と定常波
入射波と反射波が重ね合わさり、波を形成していきます。
・自由端反射
入射波$y_i=A\sin{2π(\frac{t}{T} – \frac{x}{λ})}$と 反射波$y_r=A\sin{2π(\frac{t}{T} – \frac{2L-x}{λ})}$を足し合わせると、
三角関数の合成$\sin{α}+\sin{β}=2\sin{(\frac{α+β}{2})}\cos{(\frac{α-β}{2})}$から
$$y ( {\color{orange} t} , {\color{green} x}) = 2A\sin{2π(\frac{ {\color{orange} t} }{T} – \frac{L}{λ})} \cos{2π(\frac{L- {\color{green} x} }{λ})} $$
となり、これが定常波と呼ばれる式が導けました。
時間の変数は$\sin{}$の式、位置の変数は$\cos{}$の式として分離できています。
ある時刻$t$での振幅$ {\color{orange} D(t) } = 2A\sin{2π(\frac{ {\color{orange} t} }{T} – \frac{L}{λ})} $ とすると
$$y = {\color{orange} D(t) } \cos{2π(\frac{L- {\color{green} x} }{λ})} $$
となります。つまりどの時刻であっても波の形(腹と節の位置)は変わらず、振幅だけが時間と共に変化します。
自由端反射の場合は、端が常に振幅と同じ$D(t)$となるため、定常波の腹となります。
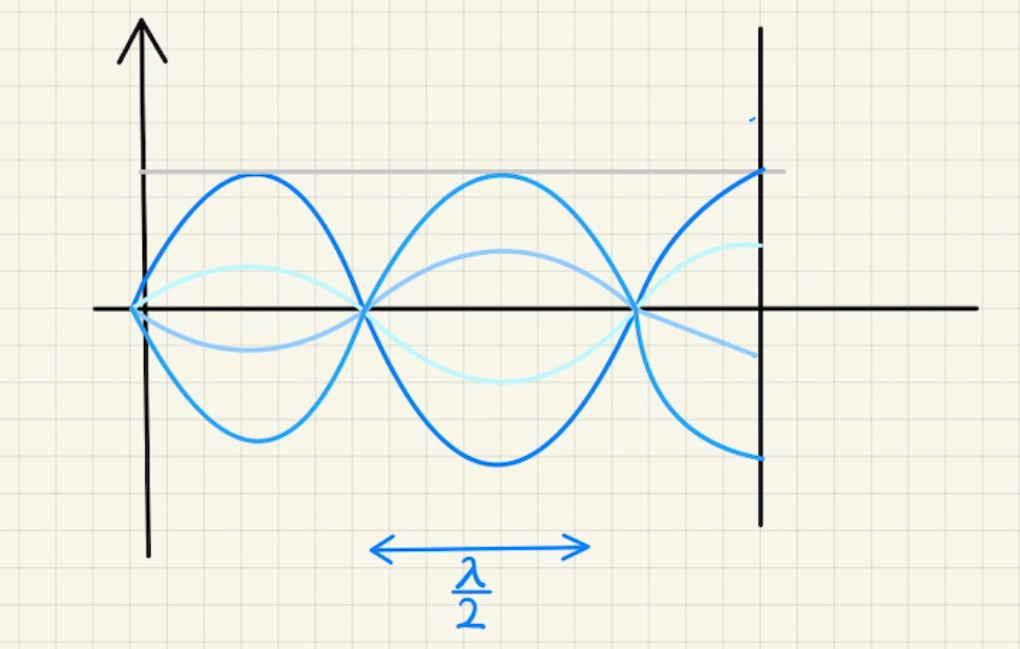
・固定端反射
先ほどと同様に、入射波$y_i=A\sin{2π(\frac{t}{T} – \frac{x}{λ})}$と 反射波$y_r=-A\sin{2π(\frac{t}{T} – \frac{2L-x}{λ})}$を足し合わせると、三角関数の合成から
$$y ( {\color{orange} t} , {\color{green} x}) = 2A\cos{2π(\frac{ {\color{orange} t} }{T} – \frac{L}{λ})} \sin{2π(\frac{L- {\color{green} x} }{λ})} $$
となり、 振幅$ {\color{orange} D(t) } = 2A\cos{2π(\frac{ {\color{orange} t} }{T} – \frac{L}{λ})} $とおけば、
$$y = {\color{orange} D(t) } \sin{2π(\frac{L- {\color{green} x} }{λ})} $$
となります。
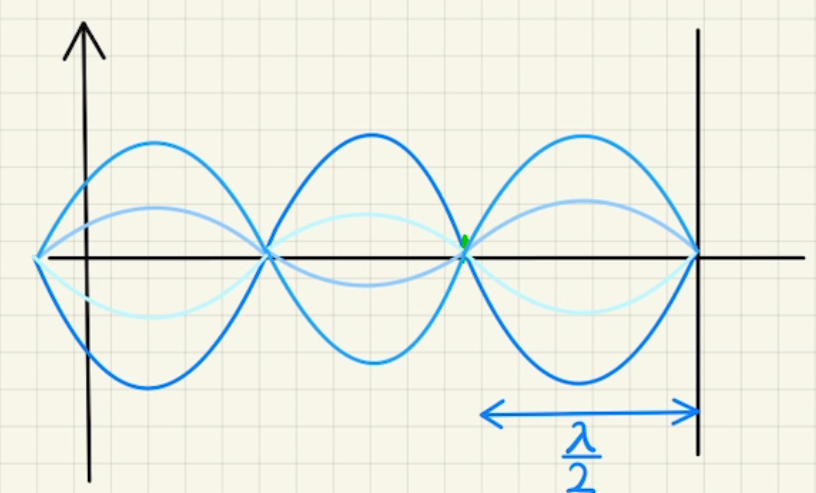
固定端反射の場合は、端が常に$0$となるため、定常波の節となります。
横波と縦波(疎密波)
今まで、考えてきた波は主に横波のイメージだったでしょう。
しかし、空気などの流体の疎と密も波と言えそうです。
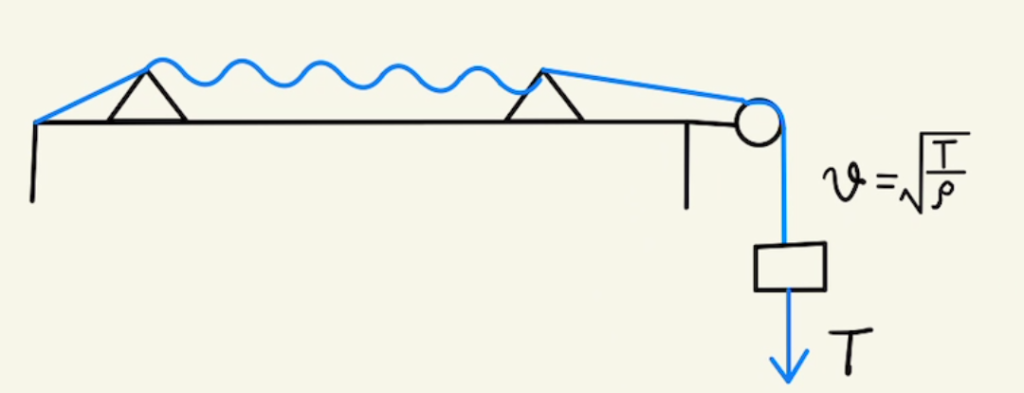
・横波
一般的にイメージできる波と近いです。
弦の振動などがこれに相当します。
・縦波(疎密波)
流体やゴム等で、進む方向の疎と密によって構成される波です。
地震の揺れは基本的に横波ですが、発生と同時にP波と呼ばれる疎密波も同時に発し、P波の方が速いため数秒先に届くので緊急地震速報などに用いられています。
グラフに書く場合は均等である流体とのズレを$y$として表します。
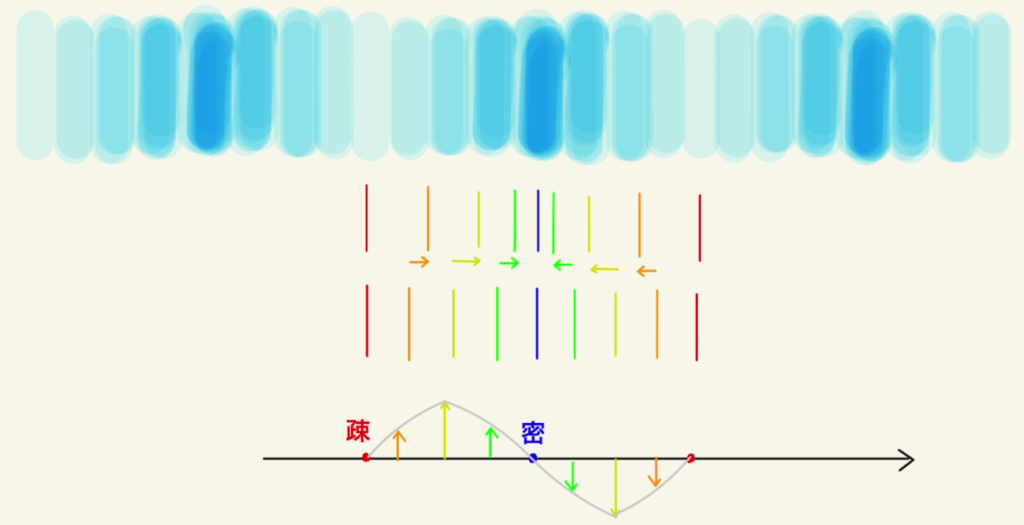
疎と密なところではズレはないため$y=0$、つまり節となります。
一方で疎でも密でもない部分(外部の気圧と同じ部分)は腹となります。
傾きがプラスの場合は、流体が外に出ていく向きでの動き大きいため、最も疎になります。←|→
傾きがマイナスの場合は、流体が内側に入ってくる向きでの動きが大きいため、最も密になります。 →|←
気柱
ある長さの気柱(管)に対して音を入れるとある波長でだけ共振を起こします。
笛等の管楽器ではこれを利用して特定の波長だけを大きくしています。
・閉管
片側が閉まっている気柱です。空気を振動させると端で固定端反射をします。
気柱の長さを$l$とすると気柱の出口の少し先で疎でも密でもないニュートラルな状態になると共振します。
この出口部分のズレを開口端補正といいます。 開口端補正は気柱の半径より少し小さいくらいだといわれています。
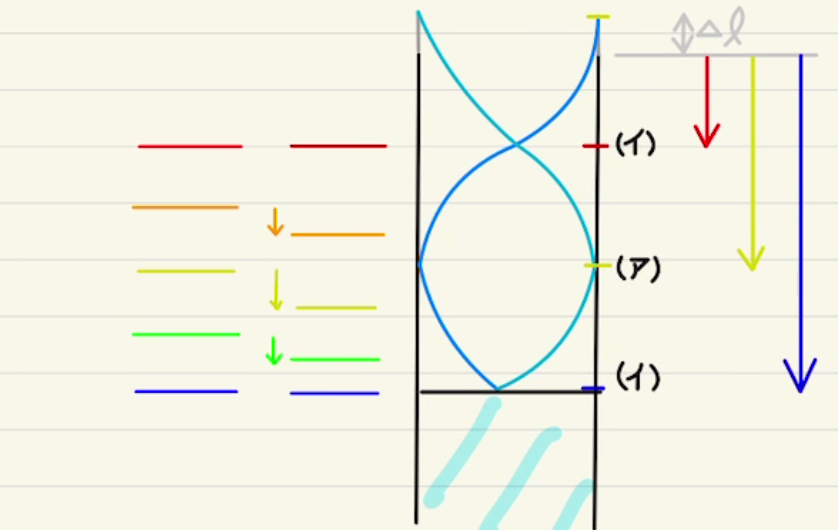
開口端補正を$Δl$とすると、共振する条件は下のようになります。
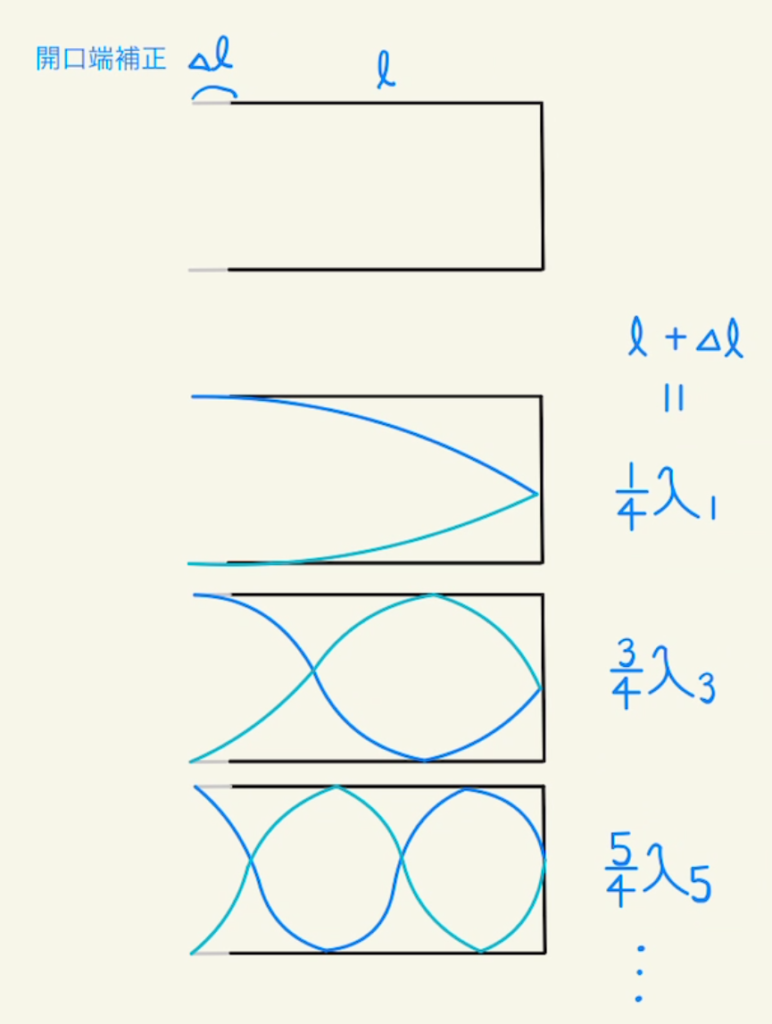
これを一般化すると
$$l+Δl=\frac{2n-1}{4}λ_{2n-1}$$
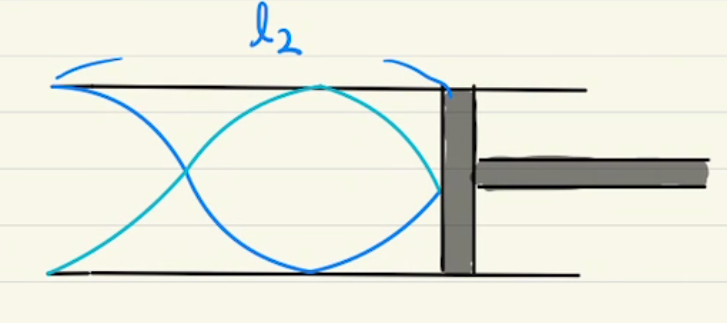
・開管
両端が開いている気柱です。
両端の気柱の出口の少し先で疎でも密でもないニュートラルな状態でなると共振します。
共振する条件は下のようになります。
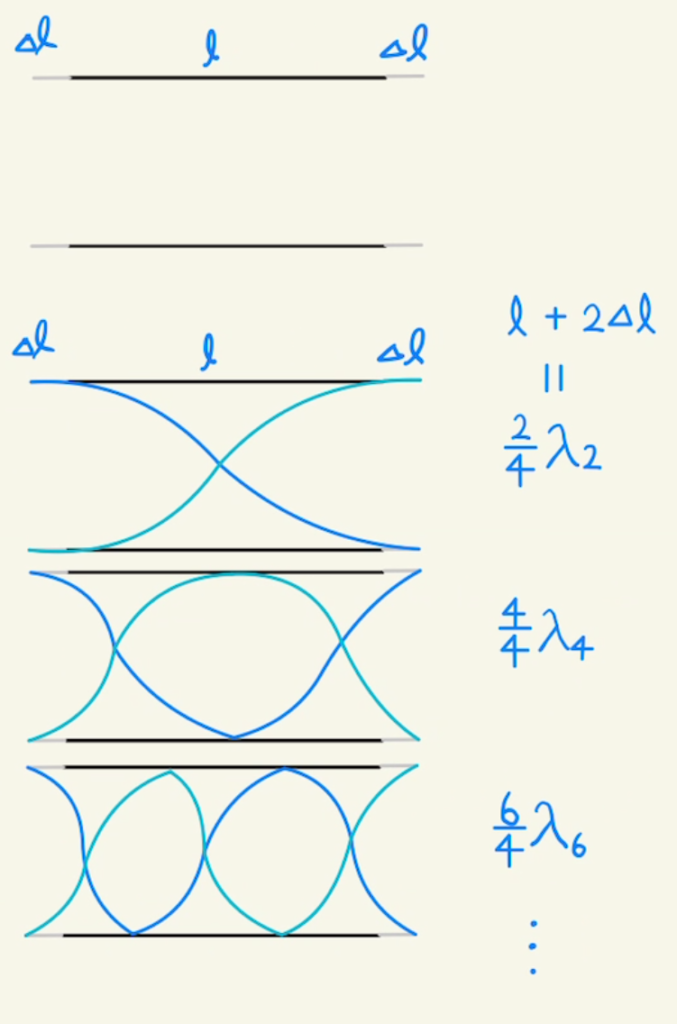
これを一般化すると
$$l+2Δl=\frac{2n}{4}λ_{2n}$$
まとめ
波は一般的に下の式で表せる。
$$ y( t , x) = A\sin{2π(\frac{ t }{T} – \frac{ x }{λ})}$$
波が端にあたって反射する場合、自由端反射と固定端反射がある。
・自由端反射はそのままの波が反射され、合成によって生まれた定常波は端が腹となる。
・固定端反射は逆さまになった波が反射され、合成によって生まれた定常波は端が節となる
流体等の疎と密によって構成された縦波(疎密波)も存在する。
流体の位置のズレをグラフとして記すが、疎と密では$y=0$の節となり、傾きが正なら疎、傾きが負なら密。
気柱では一部の波長で共振を起こす。
気柱の長さを$l$、開口端補正を$Δl$とすると共振を起こす波長$λ$の条件は
閉まっていたら固定端反射となり、$l+Δl=\frac{2n+1}{4}λ_n$
開いていたら自由端反射となり、$l+2Δl=\frac{2n}{4}λ_n$