解答欄
(1)
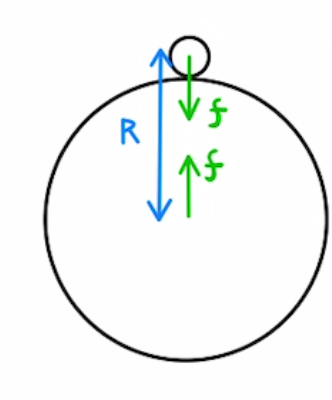
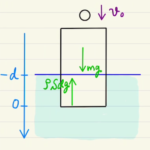
地表での万有引力
$f = G\frac{mM}{R^2}$
これが地表での重力$mg$に相当するため
$ g=G\frac{M}{R^2} $
(2)
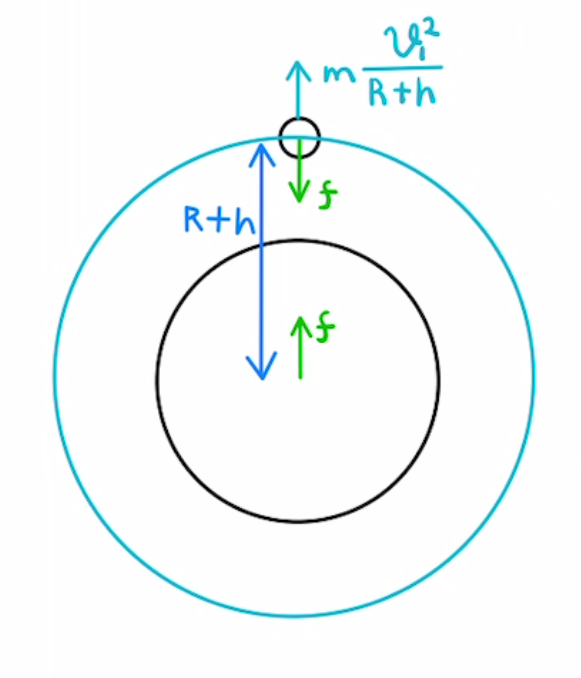
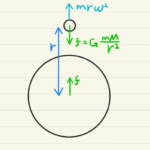
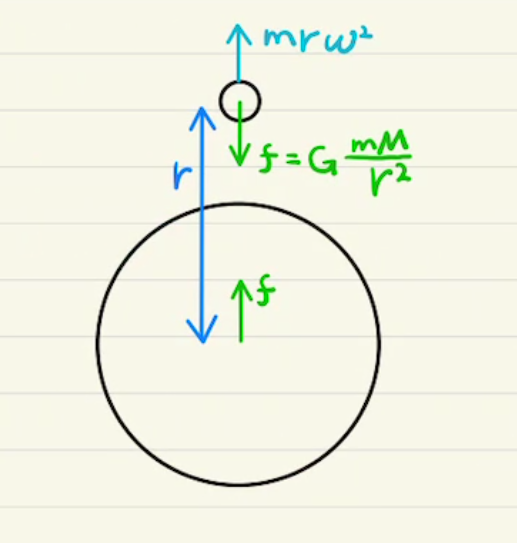
地上からの高さが$h$のとき地球の重心からの距離は$R+h$となるから万有引力は
$ f = G \frac{M}{(R+h)} $
これが遠心力$m\frac{v^2}{(R+h)^2}$と釣り合うため
力のつり合い
$m・0 = m\frac{v^2}{(R+h)} \, – \, G \frac{M}{(R+h)^2} $
$∴v = \sqrt{ \frac{GM}{(R+h)} }$
周期$T$は$円軌道一周の長さ ÷ 速さ$より
$ T= \frac{2π(R+h)}{v} = 2π\sqrt{\frac{(R+h)^3}{GM}}$
(3)
$h≈0$のとき
$v_1 = \sqrt{ \frac{GM}{R} } = \sqrt{ gR } = 8.0×10^3$
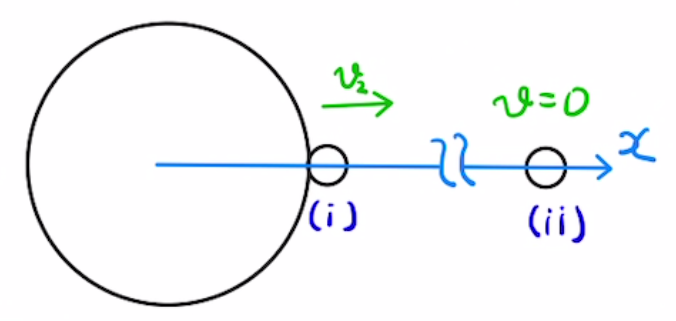
(4)
無限遠で速さ0となるようにすればよく、
力学的エネルギー保存則より
$\frac{1}{2}mv_2^2 \, – \, G \frac{mM}{R} = \frac{1}{2}m・0^2 \, – \, G \frac{mM}{∞} $
$∴v_2 = \sqrt{ \frac{2GM}{R} } = \sqrt{2gR}$