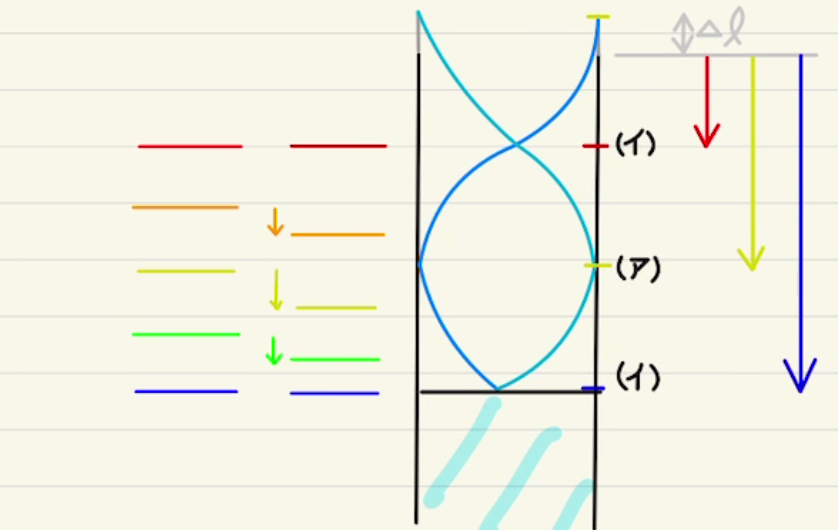
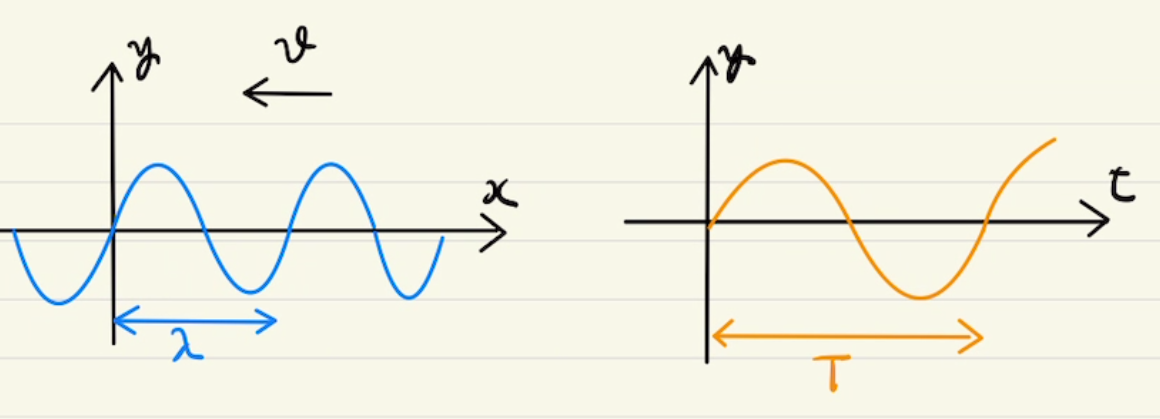解答欄
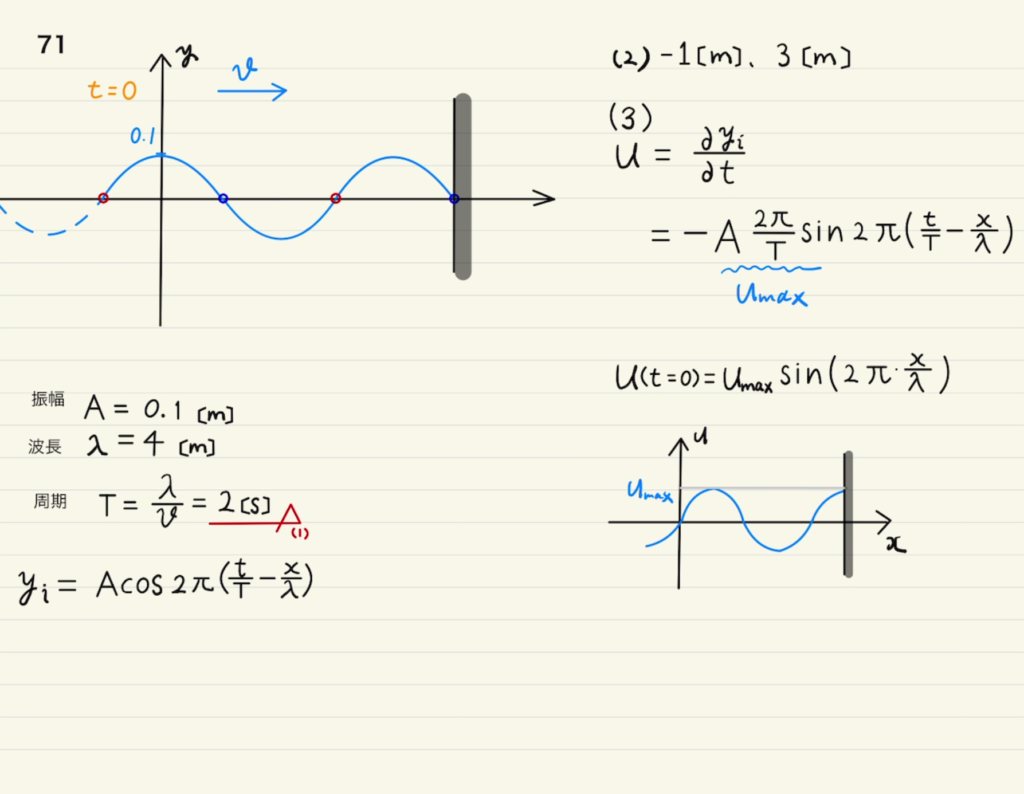
解説
右方向に進む波の問題です。
(1)一番高さがあるところが中心から0.1[m]の高さなので振幅$A=0.1[m]$
1周期(一回高くなって低くなってを)終えるまでの長さが4[m]なので、波長$λ=4[m]$
1波長分進む時間が1周期なので波長$T=\frac{λ}{v}=2[秒]$
振幅、周期、波長がわかれば式として表せます。
今回は$x=0,t=0$で最大値でスタートなので$\cos$の形になります。
波の性質の公式から波の式を表すと
$$ y_i( {\color{orange} t} , {\color{green} x}) = A\cos{\left(2π(\frac{ {\color{orange} t} }{T} – \frac{ {\color{green} x} }{λ})\right)} $$
の式になりますね。
$\sin$よりも位相が$\frac{π}{2}$だけ進んでいるので
$y_i( {\color{orange} t} , {\color{green} x}) = A\sin{[2π(\frac{ {\color{orange} t} }{T} – \frac{ {\color{green} x} }{λ})+ \frac{π}{2} ]} $
と書くこともできます。
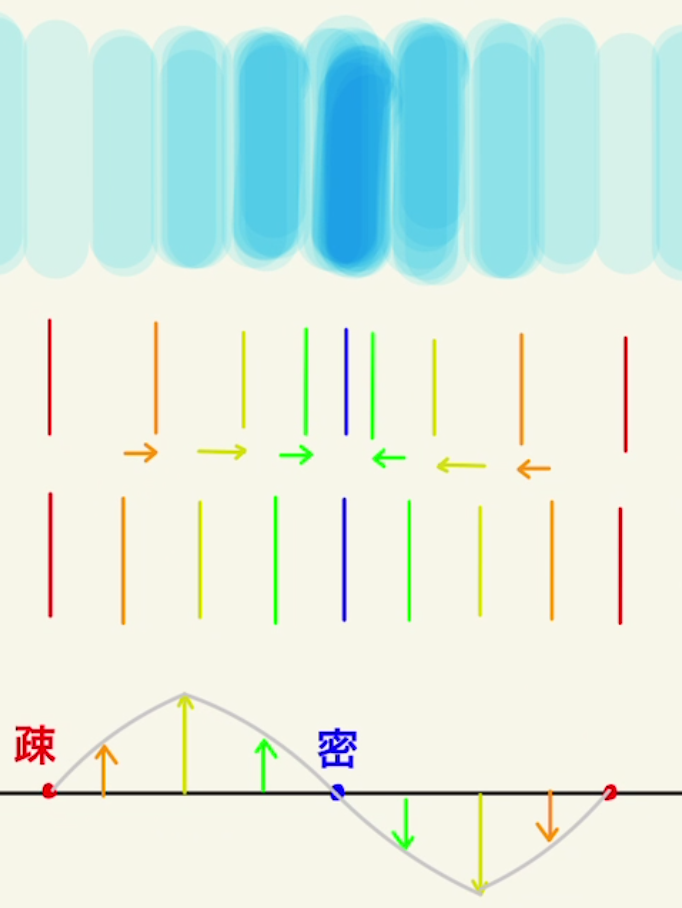
(2)疎密波では波が傾き(微分値)がプラスなら疎、マイナスなら密なことは頭に入れておきましょう。
図の赤の部分が最も疎になります。
(3)速度の定義から媒質の定義は以下のように表せます。
$$v_i( {\color{orange} t} , {\color{green} x})=\frac{∂y_i}{ ∂ t}=-A\frac{2π}{T }\sin{\left(2π(\frac{ {\color{orange} t} }{T} – \frac{ {\color{green} x} }{λ})\right)}$$
$\frac{∂y_i}{ ∂ t}$はただの微分なのですが、もう一方の変数$x$を定数とみて微分します。(偏微分)
$v_i=\frac{∂y_i}{ ∂ t}$は速度の式となり、$t=0$を代入すればその時刻の速度が求められます。
実際に代入してみると
\begin{align}
v_i( {\color{orange} t} , {\color{green} x})&= -A\frac{2π}{T }\sin{\left(2π(\frac{ {\color{orange} 0} }{T} – \frac{ {\color{green} x} }{λ})\right)}\\
&=-A\frac{2π}{T }\sin{\left( -2π\frac{ {\color{green} x} }{λ}\right)}\\
&=A\frac{2π}{T }\sin{\left( 2π\frac{ {\color{green} x} }{λ}\right)}
\end{align}
速度の最大値は$\sin$の係数についた$A\frac{2π}{T}$となります。
注:媒質(空気等)の速度は波の進む速度とは全く概念が異なります。
波の速度は振動がどれだけ早く伝わるかというものですが、これは空気そのものが移動したわけではありません。
媒質の速度のグラフのように空気(の分子)自体は同じ場所で行ったり来たりを繰り返していますが、振動を別の空気の分子が先へ先へ伝えていっているだけです。
ここでいう媒質速度とは、媒質の変位の時間微分で定義できるため、 $\frac{∂y_i}{ ∂ t}$となります。
(4),(5)は図から足し合わせで求めます。
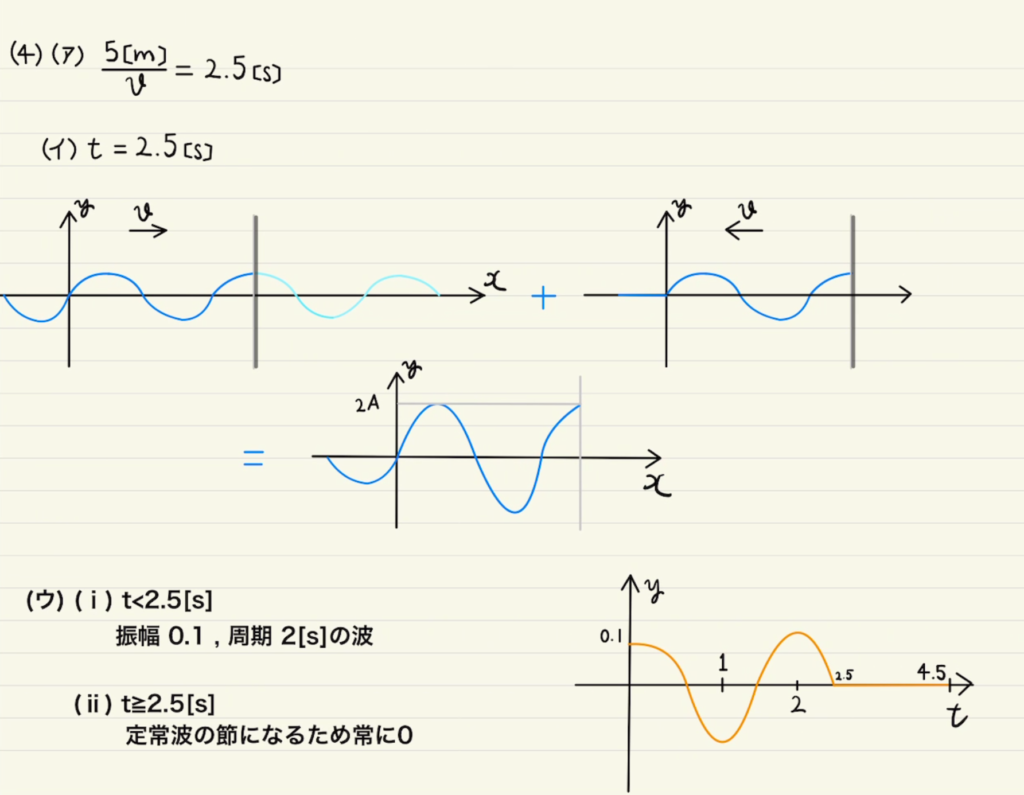
(4)壁は自由端反射なのでそのまま反対方向に反射して帰ってきます。
この入ってくる波と返ってくる波を足し合わせることになります。
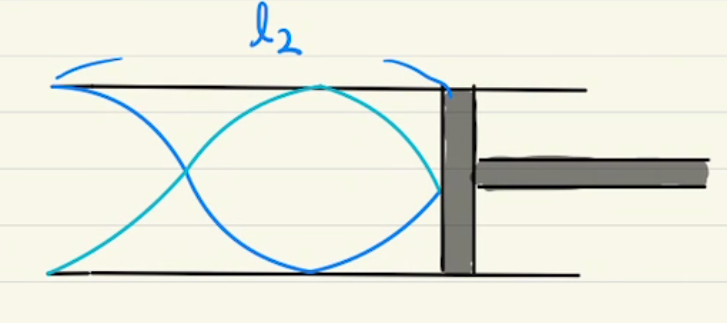
計算に関しては補足にしているので省略しますが、結果として反射した壁が腹となるような定常波になります。
ただし注意が必要なのは、反射はがまだ届いていない部分は左から来る波だけになるので、場合分けが必要です。
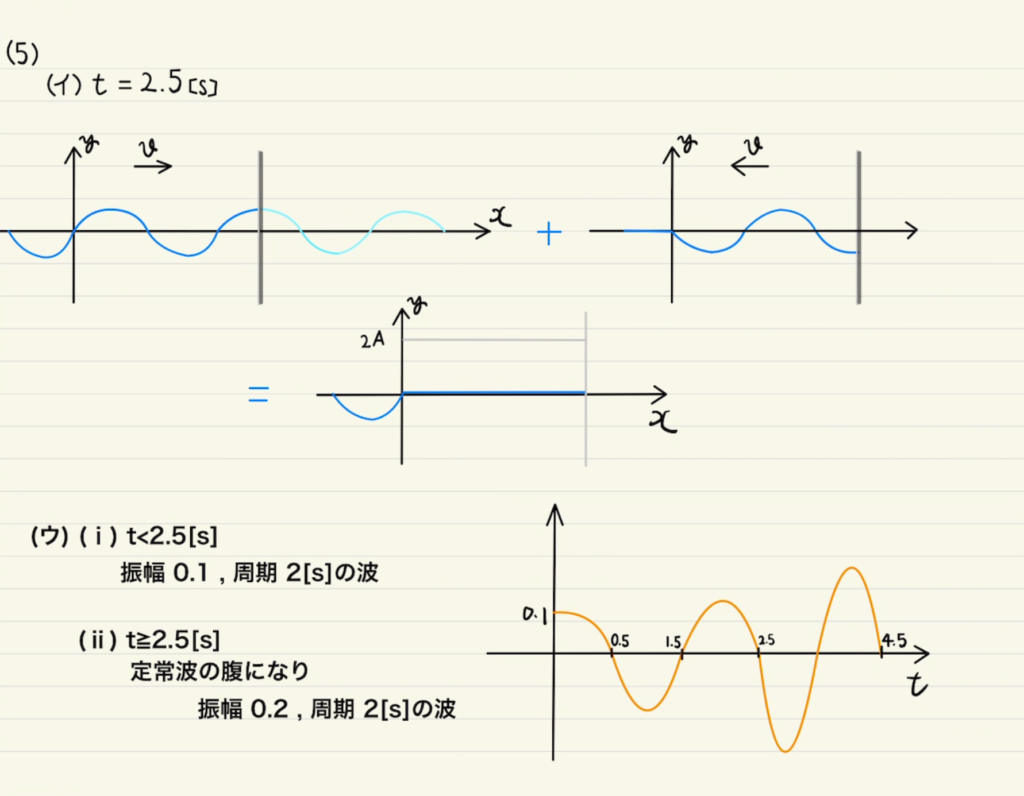
(5)壁は固定端反射なので上下逆で帰ってきます。
結果として反射した壁が節となるような定常波になります。
壁部分では0で固定されているので当然ですね。
補足
(4)(5)を数式で考えることもできます。基本的には問題を解くうえで三角関数の合成は使わないと思いますが、数式だと機械的に答えが出るので知っておくと難問で得をすることがあるかもしれません。
(4)を数式で考えると、壁の位置を$x=L(=5[m])$として、
入射波:
$ y_i( {\color{orange} t} , {\color{green} x}) = A\cos{2π(\frac{ {\color{orange} t} }{T} – \frac{ {\color{green} x} }{λ})} $
反射波($x≧0$):
$ y_r( {\color{orange} t} , {\color{green} x}) = A\cos{2π(\frac{ {\color{orange} t} }{T} – \frac{ 2L-{\color{green} x} }{λ})} $
となるので、二つの合成波は
$$ y( {\color{orange} t} , {\color{green} x}) = 2A・\cos{2π(\frac{ {\color{orange} t} }{T} – \frac{L}{λ})}・\cos{2π(\frac{L- {\color{green} x} }{λ})} $$
となります。
(イ)では$t=2.5$を代入し、
$x<0$ :
$y_i ( {\color{orange} 2.5} , {\color{green} x}) =A\sin{\frac{π}{2} {\color{green} x} } $
$x≧0$ :
$ y( {\color{orange} 2.5} , {\color{green} x}) = 2A\cos{2π(\frac{ {\color{orange} 2.5} }{2} – \frac{5}{4})} \cos{2π(\frac{5- {\color{green} x} }{4})} $
$=2A\sin{\frac{π}{2} {\color{green} x} }$
(ウ)では$x=0$を代入すればよく
$t<2.5$:
y_i ( {\color{orange} t} , {\color{green} 0}) = A\cos{2π\frac{ {\color{orange} t} }{2} } = A\cos{ π{\color{orange} t}} $
$t≧2.5$:
$ y ( {\color{orange} t} , {\color{green} 0}) = 2A・\cos{2π(\frac{ {\color{orange} t} }{T} – \frac{5}{4})}・\cos{2π(\frac{5- {\color{green} 0} }{4})}=0 $