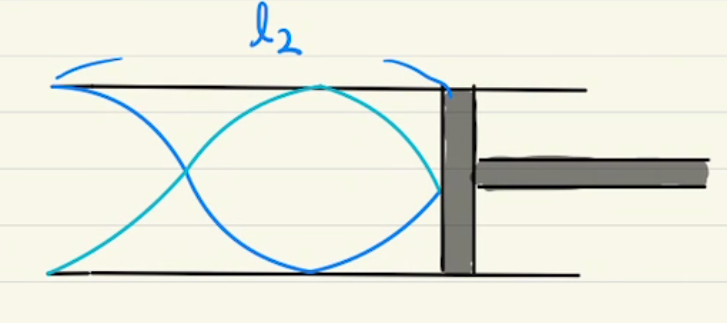
解答欄
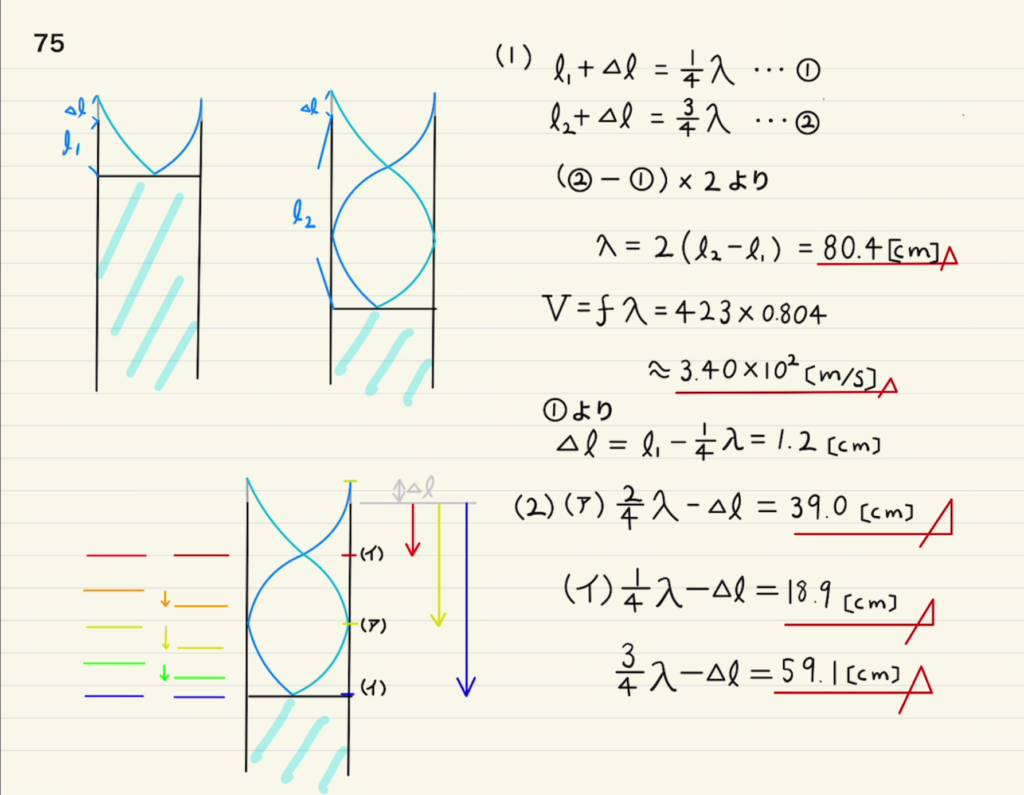
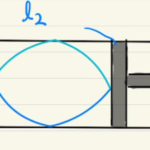
(1)二つの共鳴の式から、未知の変数$Δl,λ$を求めるというもの。
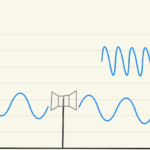
(2)振動の振幅が大きい→位置のズレ($y$の絶対値)が最大となる点(腹)
密度の変動が大きい→速度($\frac{∂y}{∂t}$の絶対値) が最大となる点(節)
と考えることができる。
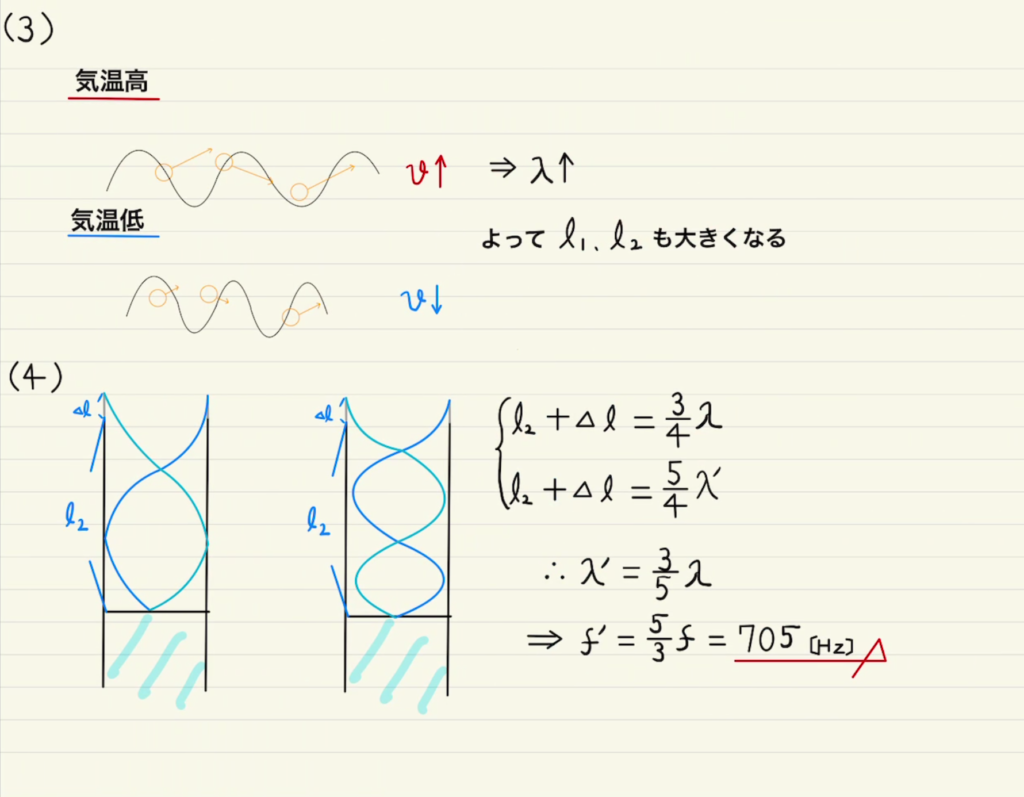
(4)次第にfを大きくした→$λ$を次第に小さくしていった、なので管長が$\frac{3}{4}λ$の時の次に波長が短くなる$\frac{5}{4}λ$で再び共鳴するようになる。
補足
気体での音の速度は
$v=\sqrt{γ\frac{RT}{M}}$ ($γ$:ポワソン比 $M$:1molの質量)
となります。(音は微小な断熱変化の連続として計算できます。)
0℃の絶対温度を$T_0(≒273.16[K])$とすると摂氏$t=T-T_0$となるから
$v=\sqrt{γ\frac{RT_0}{M}}×\sqrt{ 1+\frac{t}{T_0} } $
となるため、$t$の関数として1次近似を使うと
$v=\sqrt{γ\frac{RT_0}{M}}×(1+\frac{t}{2T_0}) $
となります。 ($|t|<<T_0$のとき)
実際に空気で計算してみると、窒素:酸素=4:1の混合気体として、平均分子量$M=28.8[g/mol]$ ポワソン比$γ=1.4$となるから
$v=331.5 + 0.6t$
となります。