名問の森Ⅰ 36 解説

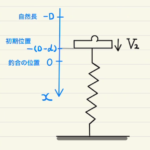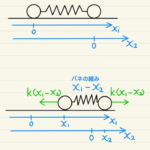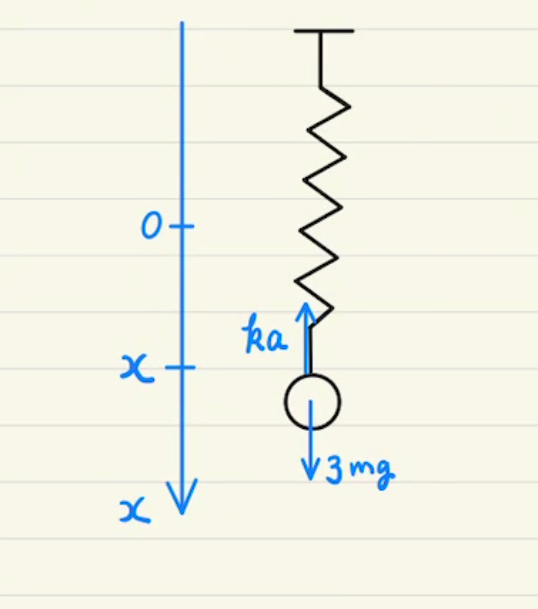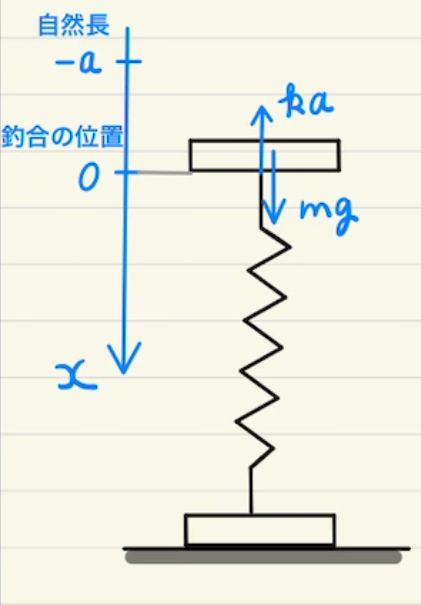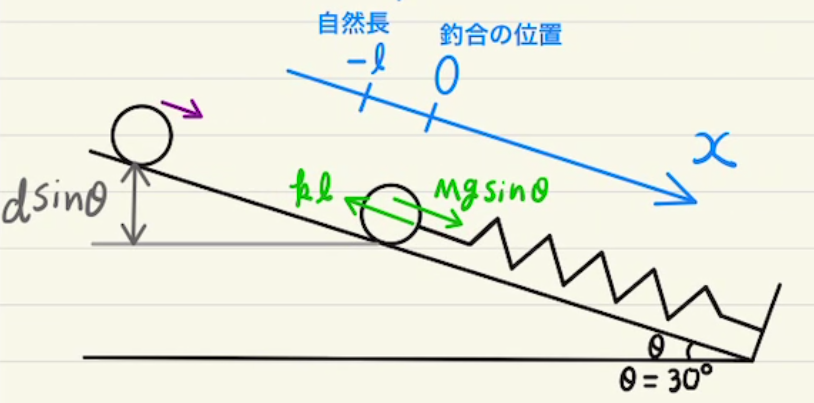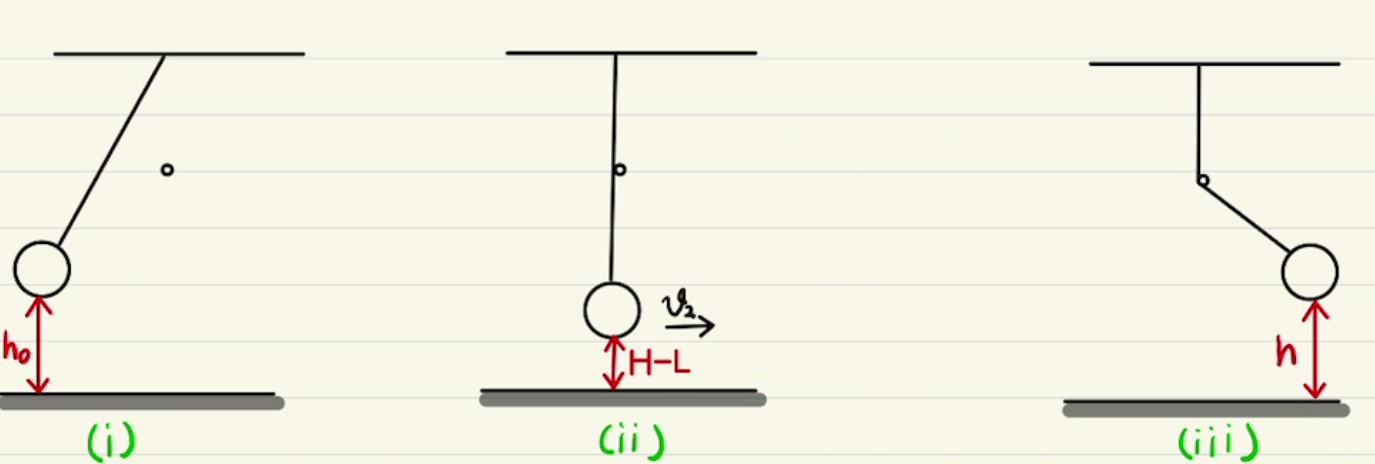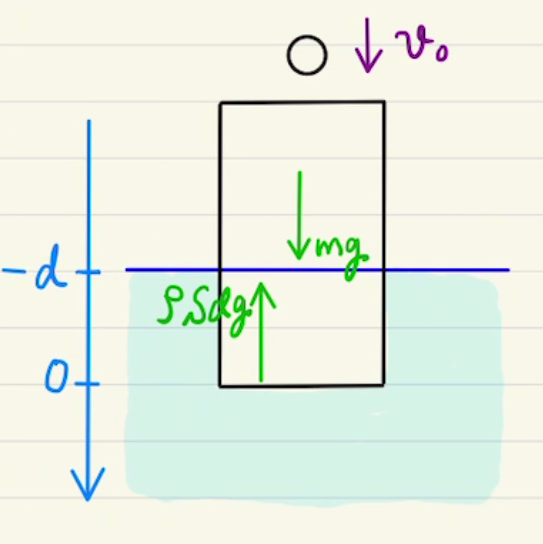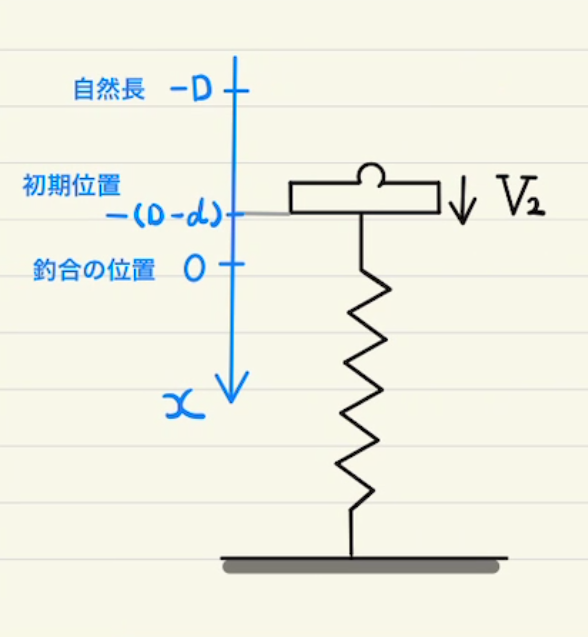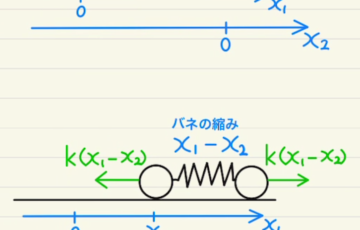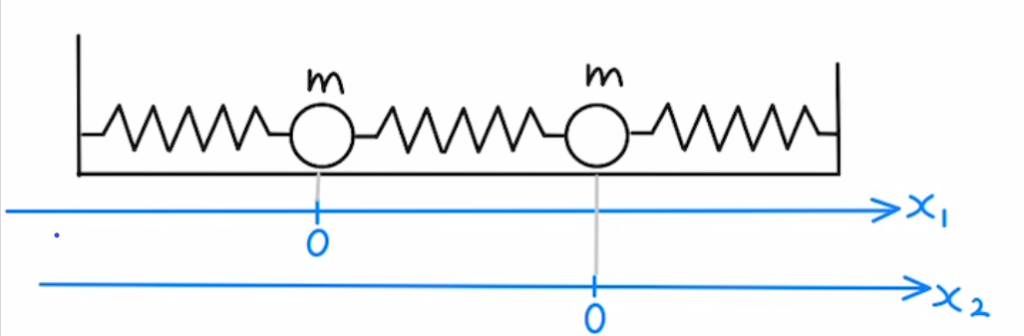
図のようにバネが全て自然長であるときの位置が原点になるように、Aの位置を$x_1$, Bの位置を$x_2$と設定します。

(1)

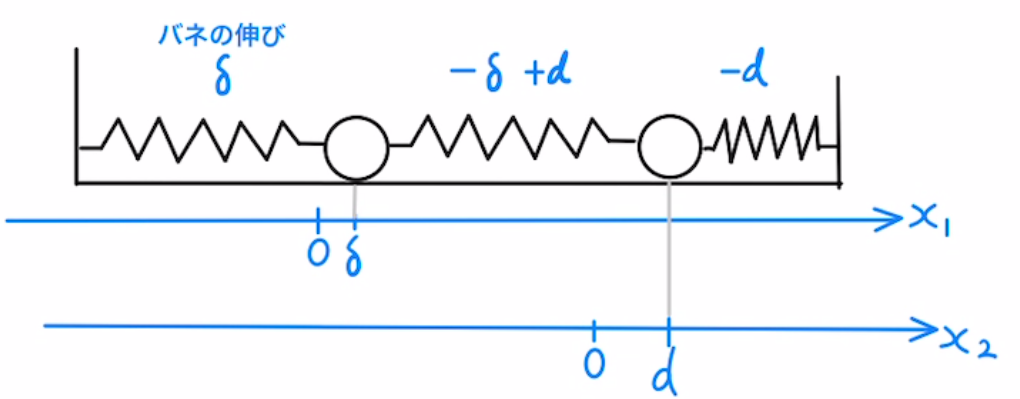
上図のように$x_2=d$、$x_1=\delta$で静止しているとします。
すると、三つのバネの伸びはそれぞれ$\delta ,-\delta +d,-d$となります。

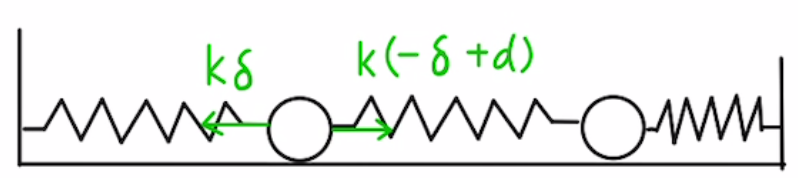
Aの力のつり合い
$m\mathrm{・}0=k(d-\delta )-kd$
より$\delta =\frac{d}{2}$

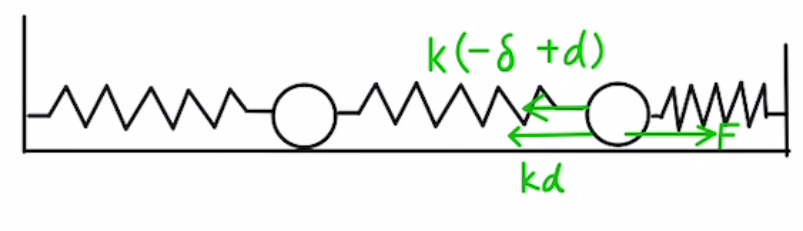
Bの力のつり合い
$m\mathrm{・}0=F-k(d-\delta )-kd$
より$F=\frac{3}{2}kd$
となります。

(2)

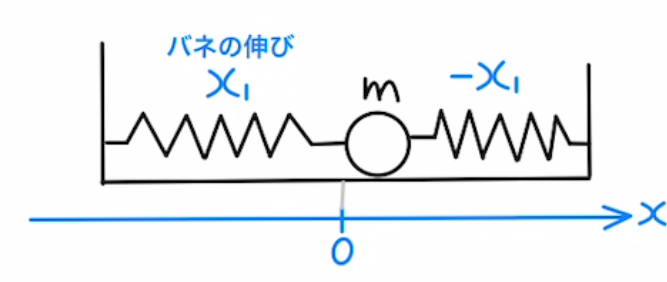
Bは固定されているため、AとAの両端のバネについてのみ考えればよい。

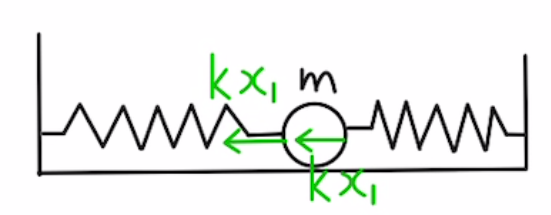
このとき、それぞれのバネの伸びは$x_1,-x_1$と書けるため、
Aの運動方程式は
$$m\ddot{x_1}=-k{x}_1-k{x}_1$$

となり、
$$\ddot{x_1}=-\frac{2k}{m}{x}_1$$
と書き換えられます。
ここで各振動数$\omega =\sqrt{\frac{2k}{m}}$と置きます。
$x_1(0)=d,v_1(0)=0$から、この微分方程式を解くと、(参考)
$$x_1(t)=x(0)\cos \omega t+\frac{v(0)}{\omega }\sin \omega t =d\cos \omega t$$
これを時間で微分すると
$$v_1=–d\omega \sin \omega t$$
となります。

これらの式から周期は
$$T_2=\frac{2\pi }{\omega }=2\pi \sqrt{\frac{m}{2k}}$$
また、$x_1=0$のとき$\cos \omega t=0$、すなわち $|\sin \omega t|=1$なので
速さは
$$|v_1|=d\omega =d\sqrt{\frac{2k}{m}}$$
となります。

(3)問題に入る前にまず、一般的な状況を考えてみましょう。
つまり、AとBは固定されておらずそれぞれ位置が$x_1,x_2$であったときの運動方程式を立てます。

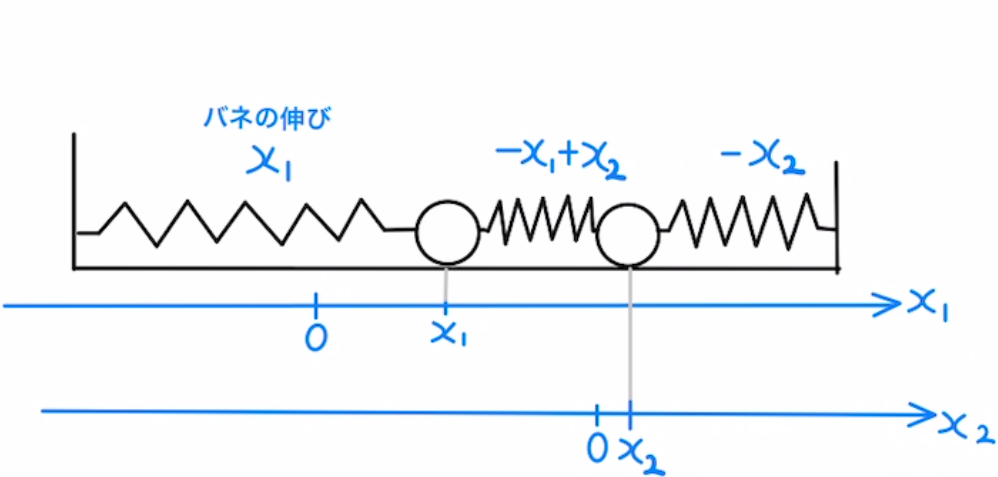
上図は全てバネが伸びたときの力の方向となっていますが、状況によって変わります。

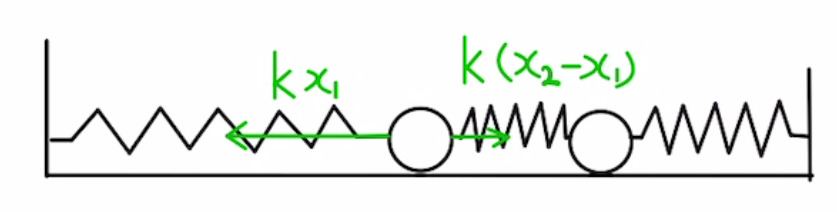
Aの運動方程式は
$$m\ddot{x_1}=-k{x}_1+k(x_2-x_1)$$
より
$$\ddot{x_1}=-\frac{k}{m}(2x_1-x_2) \mathrm{①}$$

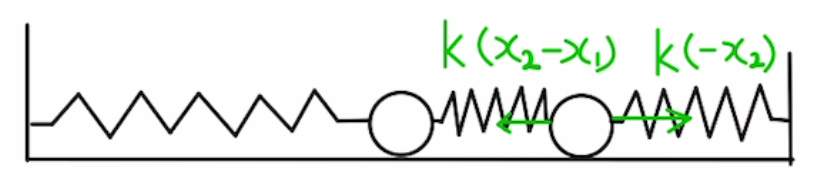
Bの運動方程式は
$$m\ddot{x_2}=-k(x_2-x_1)-k{x}_2$$
より
$$\ddot{x_2}=-\frac{k}{m}(2x_2-x_1) \mathrm{②}$$

①,② の連立微分方程式を解くことになります。
解き方は連立漸化式と非常によく似ています。

すなわち$x_1+r{x}_2=-{\omega }^2(x_1+r{x}_2)$となる$r$を二つ見つけだして単振動の式として解きます。
実際に$\mathrm{①}+r\times \mathrm{②}$から条件を満たすものを探すと$r=1,-1$ となり、それらを記述すると、

$$\begin{array}{r}\{\begin{array}{l}\ddot{x_1}+\ddot{x_2}=-\frac{k}{m}(x_1+x_2) \mathrm{①}+\mathrm{②}\\ \ddot{x_1}-\ddot{x_2}=-\frac{3k}{m}(x_1-x_2) \mathrm{①}-\mathrm{②}\end{array}\end{array}$$
ここで$X_1=x_1+x_2, X_2=x_1-x_2$ と置くと
$$\text{Math input error}$$
あとは通常の単振動の問題となります。

まずの方程式は、${\omega }_1=\sqrt{\frac{k}{m}}$
と置くと
$$X_1(t)=X_1(0)\cos {\omega }_{1}t+\frac{V_1(0)}{{\omega }_1}\sin {\omega }_{1}t$$
となります。

同様に の方程式は、${\omega }_2=\sqrt{\frac{3k}{m}}$
と置くと
$$X_2(t)=X_2(0)\cos {\omega }_{2}t+\frac{V_2(0)}{{\omega }_2}\sin {\omega }_{2}t$$
となります。

この二式から$x_1$と $x_2$を逆算していけます。

それぞれの条件から初期条件を見ていきましょう。
(3)の場合、$x_1(0)=d,x_2(0)=d,v_1(0)=0,v_2(0)=0$となることから、
$X_1(0)=2d,X_2(0)=0,V_1(0)=0,V_2(0)=0$ となり、,に代入すると
$$\begin{array}{r}\{\begin{array}{l}{X}_1(t)=d\cos {\omega }_{1}t \\ X_2(t)=0 \end{array}\end{array}$$
となります。
よってAの位置は
$$x_1=\frac{X_1(t)+X_2(t)}{2}=d\cos {\omega }_{1}t$$
周期は$$T_3=\frac{2\pi }{{\omega }_1}=2\pi \sqrt{\frac{m}{k}}$$

これらの式からわかることは、AとBが全く同じように動き、間のバネは常に自然長のまま動きます。
直観的にも正しそうですね。

(4)の条件では、 $x_1(0)=d,x_2(0)=-d,v_1(0)=0,v_2(0)=0$となることから、
$X_1(0)=0,X_2(0)=2d,V_1(0)=0,V_2(0)=0$ となり、,に代入すると

$$\begin{array}{r}\{\begin{array}{l}{X}_1(t)=0 \\ X_2(t)=2d\cos {\omega }_{2}t \end{array}\end{array}$$
となります。
よってAの位置は
$$x_1=\frac{X_1(t)+X_2(t)}{2}=d\cos {\omega }_{2}t$$
周期は$$T_4=\frac{2\pi }{{\omega }_2}=2\pi \sqrt{\frac{m}{3k}}$$

この式から、中央で鏡合わせのような動きをすることがわかります。(線対称)　

これが(3),(4)を運動方程式から解く手順となります。
今回はどちらも初期条件が対称的であるため、どのような動きをするのかは予測がつけられると思います。
ただ今回のような方法も見ておくことで、どんな複雑な問題であっても解くことが可能です。