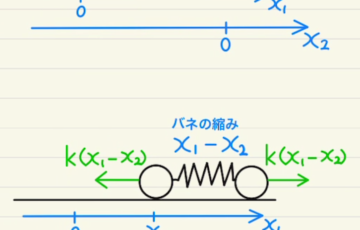
解答欄


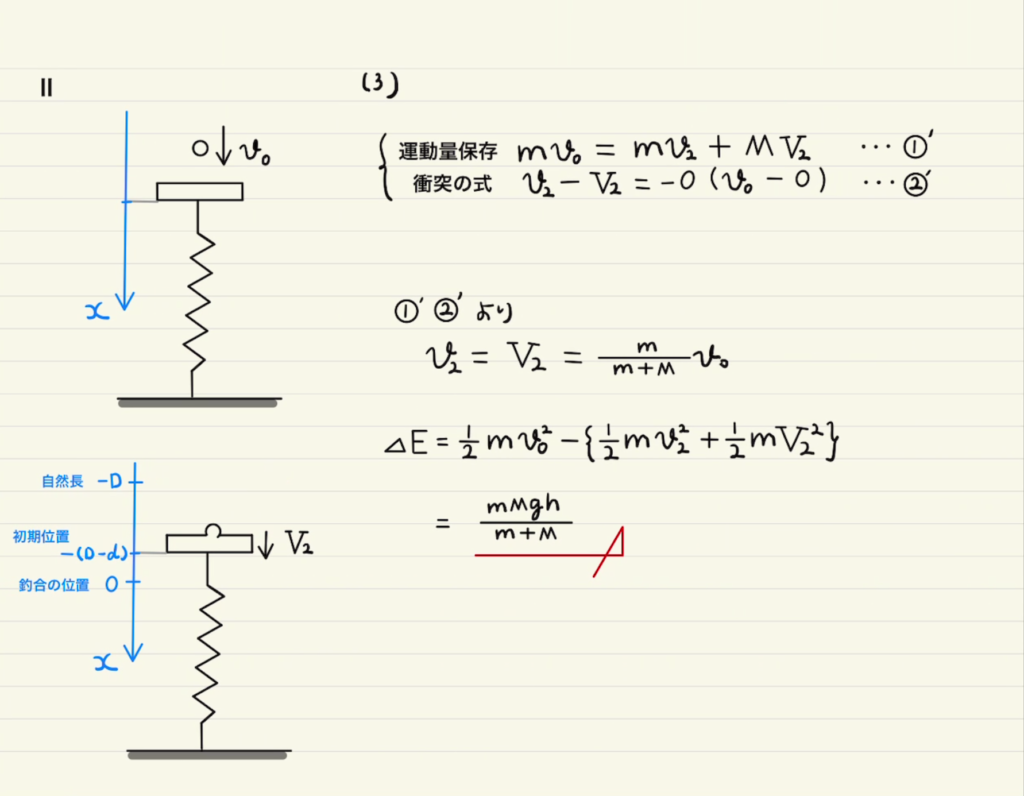

解説
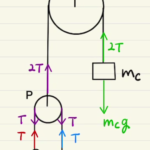
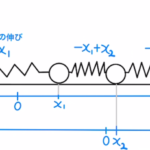
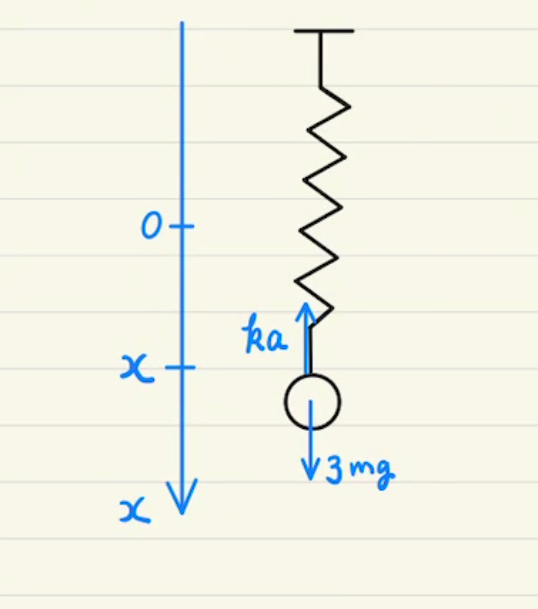
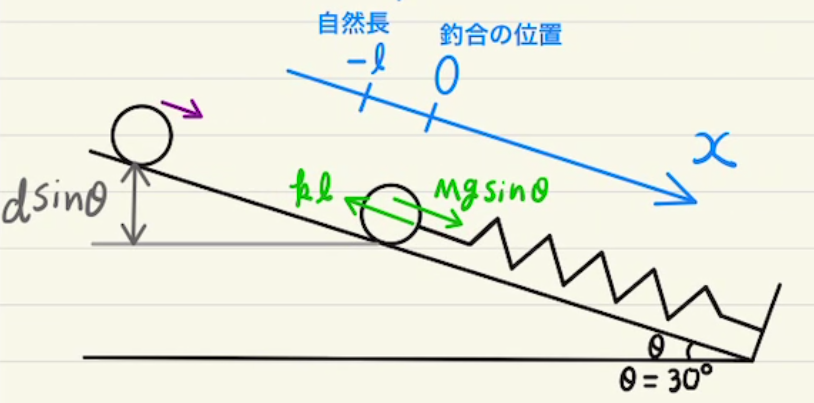
バネによる振動の問題となります。
典型的な問題では、初速度が0で静かに離して動きだすか、振動中心で初速度を与えて動き出す問題ばかりでした。
このとき、振動の基本式
$$x(t) = x(0) \cos{ωt} + \frac{v(0)}{ω}\sin{ωt}$$
の$ \cos{ωt} $もしくは$ \sin{ωt} $の係数が0になり、計算もしやすいものでした。
しかし、今回のⅡはどちらの係数も0になることはなくなります。
このとき、二つの解き方が考えられます。
一つは三角関数の合成です。
こちらは振動の基本式を
$$x(0) \cos{ωt} + \frac{v(0)}{ω}\sin{ωt}= \sqrt{ x(0) ^2 + ( \frac{v(0)}{ω} )^2} \cos{(ωt+Φ)} $$
と計算できます。
今回は使いませんが、$Φ$は初期位相で、 $ \cos{ Φ } = \frac{ \frac{v(0)}{ω} }{ \sqrt{ x(0) ^2 + ( \frac{v(0)}{ω} )^2} } $となります。
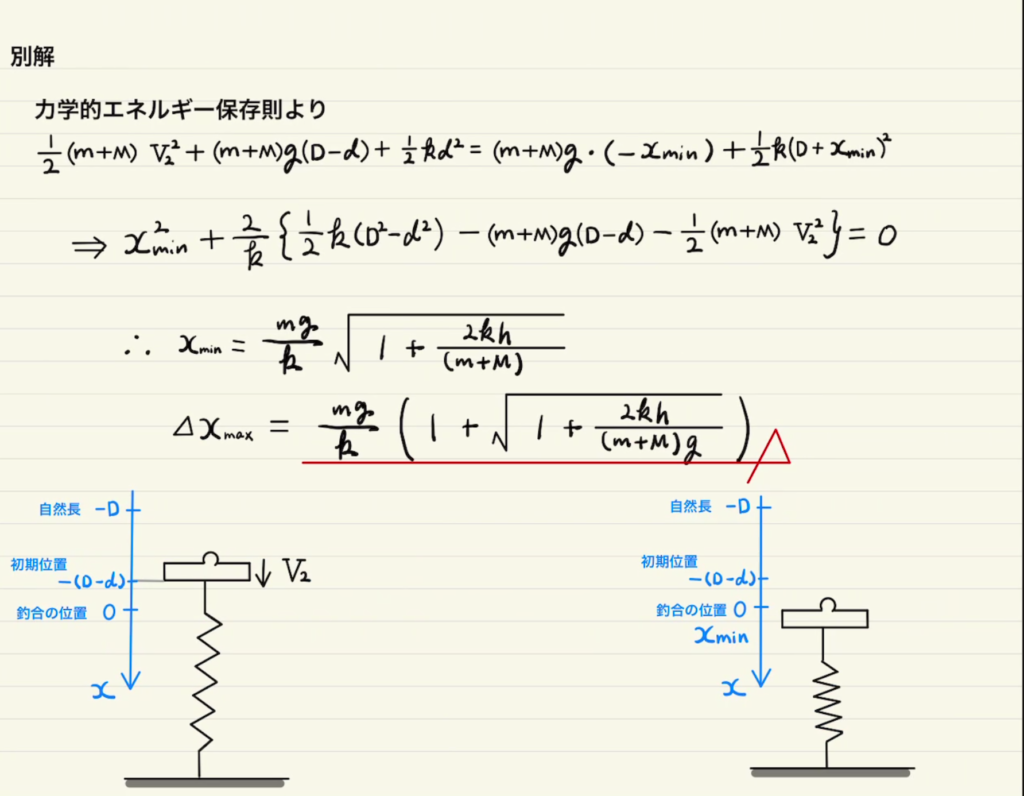
もう一つは力学的エネルギー保存の式です。(別解)
こちらを使う場合は運動エネルギー、位置エネルギー、弾性エネルギーをもれなく記載しましょう。
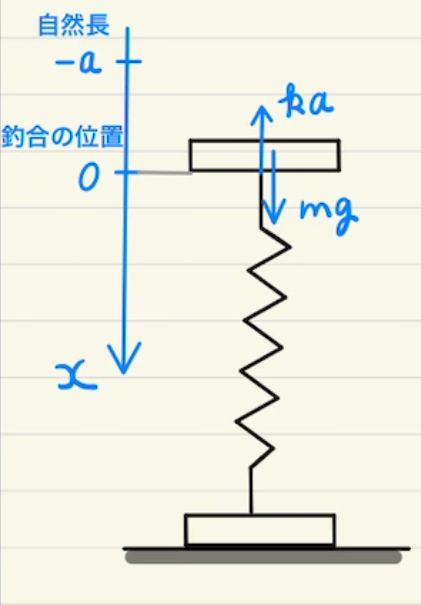
どこを位置エネルギーの基準にするかは間違わないようにしましょう。
(解答にはA方式だとかB方式だとか書いてありますがこの分け方はオススメしません。A方式は弾性エネルギーと位置エネルギーを合計して平方完成したものを疑似的な弾性エネルギーとして扱っているようですが、混同の元となります。)
二つを比べて、個人的には前者の三角関数の合成をお勧めします。今回は聞かれなかった時間経過での動きでも全て解答することが可能となり、難問に対応しやすくなります。
計算量も比較的マシになることが多いです。