(1)
反発係数1の衝突になるため、衝突前後の運動量保存から
運動量保存:$mv_0+m×0=mv_C+mv_A$
反発係数の式:$ v_C- v_A = -1(0-v_0)$
よって、$v_C=0,v_A=v_0$
(2)以降は二体の単振動の問題になります。
二物体を一つの系としたとき、($x$方向には)内部での作用反作用の力しか働かないため、運動量が保存するため重心は等速運動をします。
本来なら誘導に乗って解くこともできますが、今回は運動方程式から直接動きを見ていきましょう。
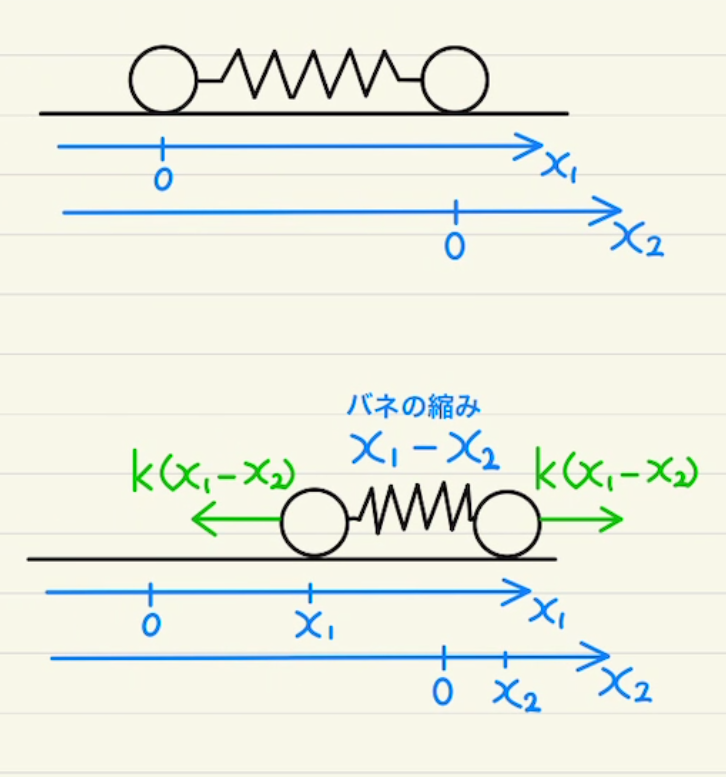
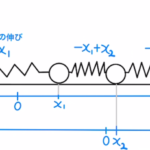
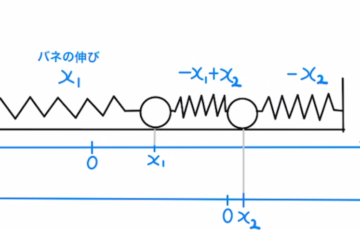
二体が動き出したあとに、Aの位置が$x_1$、Bの位置が$x_2$だけ動いたとします。すると、それぞれの加速度は$\ddot{x_1},\ddot{x_2}$となります。(点一つあたり一回時間微分)
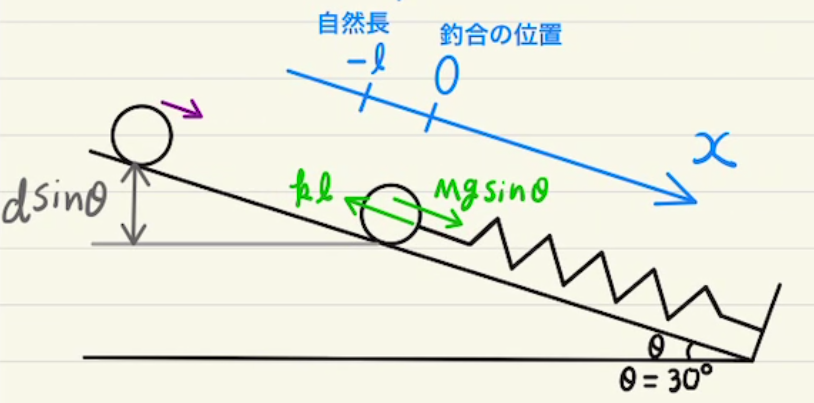
このとき、バネの縮みは$x_1-x_2$となることから、図に従ってそれぞれの運動方程式を立てると
\begin{align}
\begin{cases}
A:m\ddot{x_1} =-k( x_1-x_2 ) \\
B:m\ddot{x_2} = k( x_1-x_2 )
\end{cases}
\end{align}
これを変形すると下のようになります。
\begin{align}
\begin{cases}
\ddot{x_1} =- \frac{k}{m} ( x_1-x_2 ) ①\\
\ddot{x_2} = \frac{k}{m} ( x_1-x_2 ) ②
\end{cases}
\end{align}
この連立微分方程式を解くことになります。(連立漸化式が解き方の参考になります。)
ここでは$ ① + r×②$より$\ddot{x_1}+r \ddot{x_2} = -K( x_1+r x_2 )$となる$r$を二つ見つけだして単振動の式として解きます。
実際に求めてみると$r=1,-1$となるため、それぞれ計算してみると、
\begin{align}
\begin{cases}
\ddot{x_1}+ \ddot{x_2} = 0 \\
\ddot{x_1}-\ddot{x_2} = -\frac{2k}{m} ( x_1-x_2 )
\end{cases}
\end{align}
$X_1= x_1+x_2 , X_2= x_1-x_2$と置くと、
\begin{align}
\begin{cases}
\ddot{ X_1} = 0 \\
\ddot{ X_2} = -\frac{2k}{m} X_2
\end{cases}
\end{align}
初期条件$ x_1(0)=0,x_2(0)=0, v_1(0)=v_0,v_2(0)=0$から
$ X_1(0)=0,X_2(0)=0, V_1(0)=v_0,V_2(0)=v_0$ となり、微分方程式を解きます。(参考)
\begin{align}
\begin{cases}
X_1 = V(0)t+X(0) =v_0t \\
X_2 = X_2(0) \cos{ω_2t} + \frac{V_2(0)}{ω_2}\sin{ω_2t} = \frac{v_0}{ω_2}\sin{ω_2t}
\end{cases}
\end{align}
ただし、$ ω_2 = \sqrt{ \frac{2k}{m} }$
$X_1$が重心位置の二倍、 $X_2$がAとBの距離となっています。
ここから、$x_1,x_2$を逆算していくと
\begin{align}
\begin{cases}
x_1 = \frac{X_1+X_2}{2}= \frac{1}{2}( \frac{ v_0 }{ω_2}\sin{ω_2t} + v_0t) [1] \\
x_2 = \frac{X_1-X_2}{2} = \frac{1}{2}( – \frac{ v_0 }{ω_2}\sin{ω_2t} + v_0t ) [2]
\end{cases}
\end{align}
また、これを時間微分して速度も求められます。
\begin{align}
\begin{cases}
v_1 = \frac{1}{2}( v_0 \cos{ω_2t} + v_0) [1]’\\
v_2 = -\frac{1}{2}( v_0 \cos{ω_2t} + v_0 ) [2]’
\end{cases}
\end{align}
実際の動きは下の動画のようになります。
(2)
$$v_G=\frac{d}{dt}(\frac{x_1+x_2}{2})= \frac{V_1}{2} = \frac{V_0}{2} $$
(3)周期$T=\frac{2π}{ ω_2 }= 2π \sqrt{ \frac{m}{2k} } $となる
AB間の距離は
$$l=l_0-X_2=l_0- \frac{v_0}{ω_2}\sin{ω_2t} $$
よって、最小になるのが$ \sin{ω_2t} =1$ のとき、最大になるのが $ \sin{ω_2t} =-1$ のときで、
$l_1= l_0- \frac{v_0}{ω_2} =-v_0 \sqrt{ \frac{m}{2k} } +l_0$
$l_2= l_0+ \frac{v_0}{ω_2} =v_0 \sqrt{ \frac{m}{2k} } +l_0$
(4) [1]’ の式から
$$v_1 = \frac{1}{2}( v_0 \cos{ω_2t} + v_0) = \frac{ v_0 }{2}( \cos{( \sqrt{ \frac{2k}{m} } t)} + 1) $$