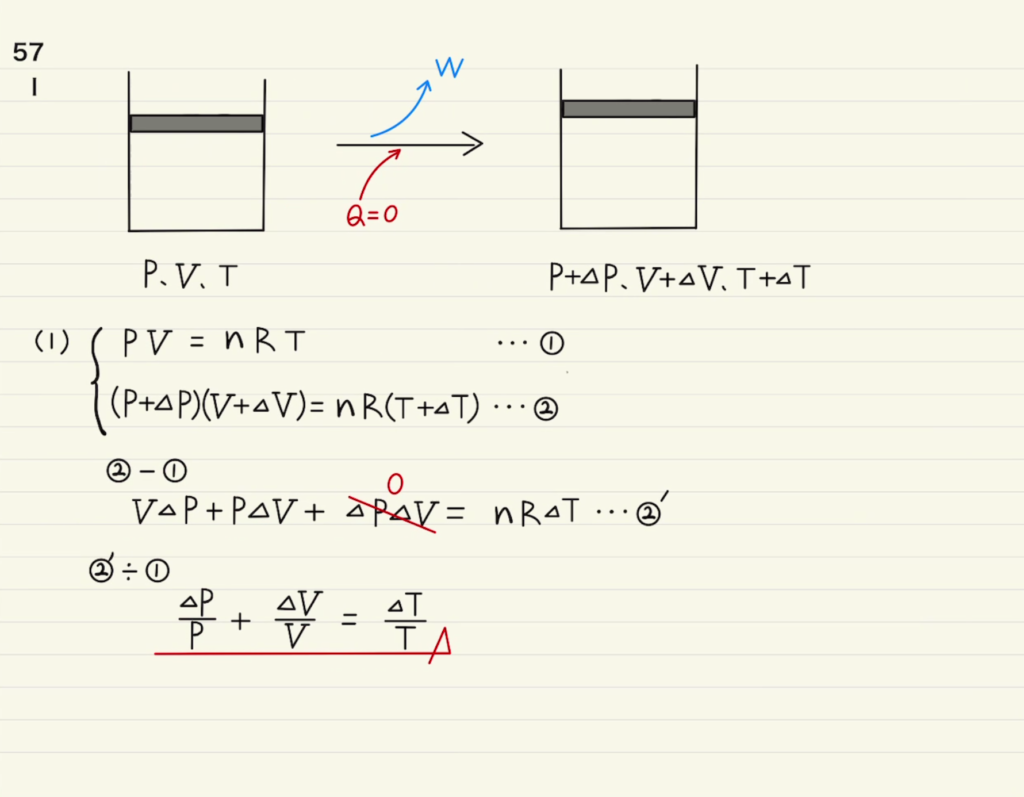
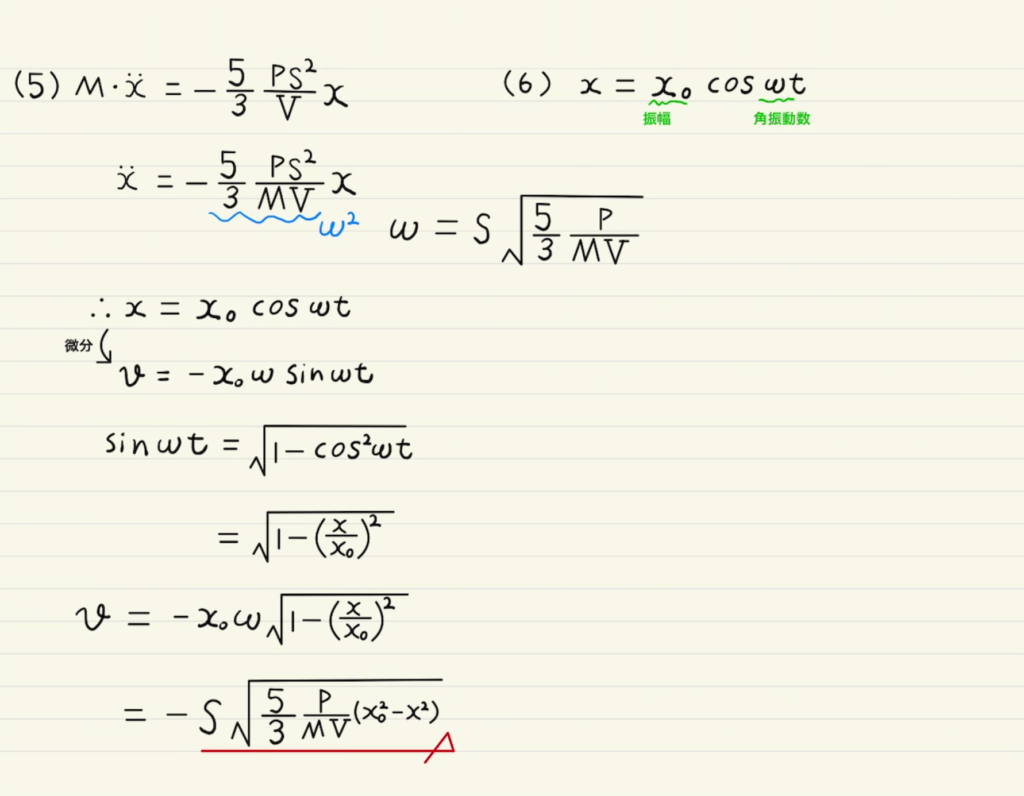
解説
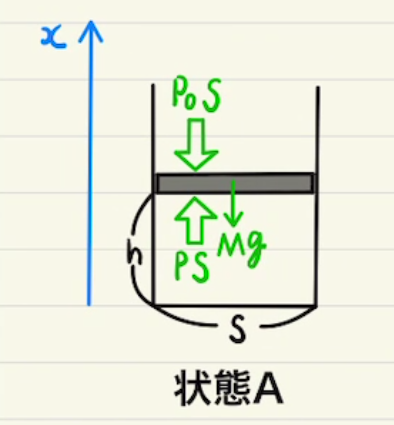
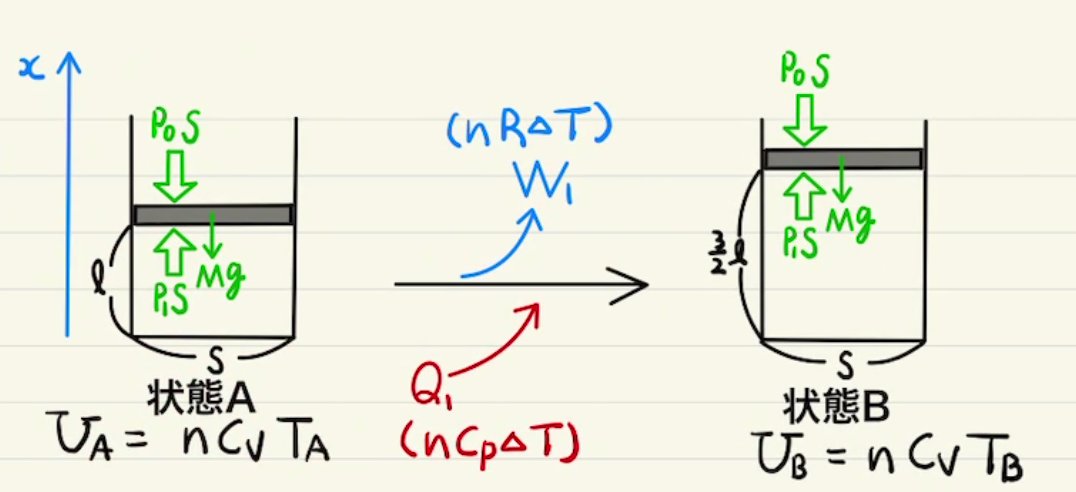
微小に状態変化させる問題となります。
気圧と体積、温度が増えたか減ったかは分からないので全て$ΔP,ΔV,ΔT$だけ増えたように記しています。もし減った場合は値がマイナスになるだけなので、とりあえずはそれで進めましょう。
この問題で重要になるのは二次の微小量、つまり$ΔP,ΔV,ΔT$のどれか二つを掛け合わせたものは$0$になることです。
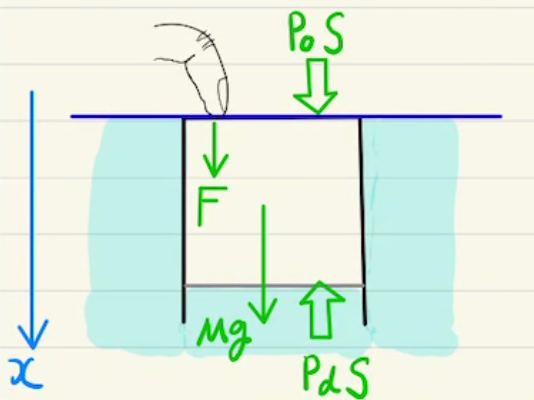
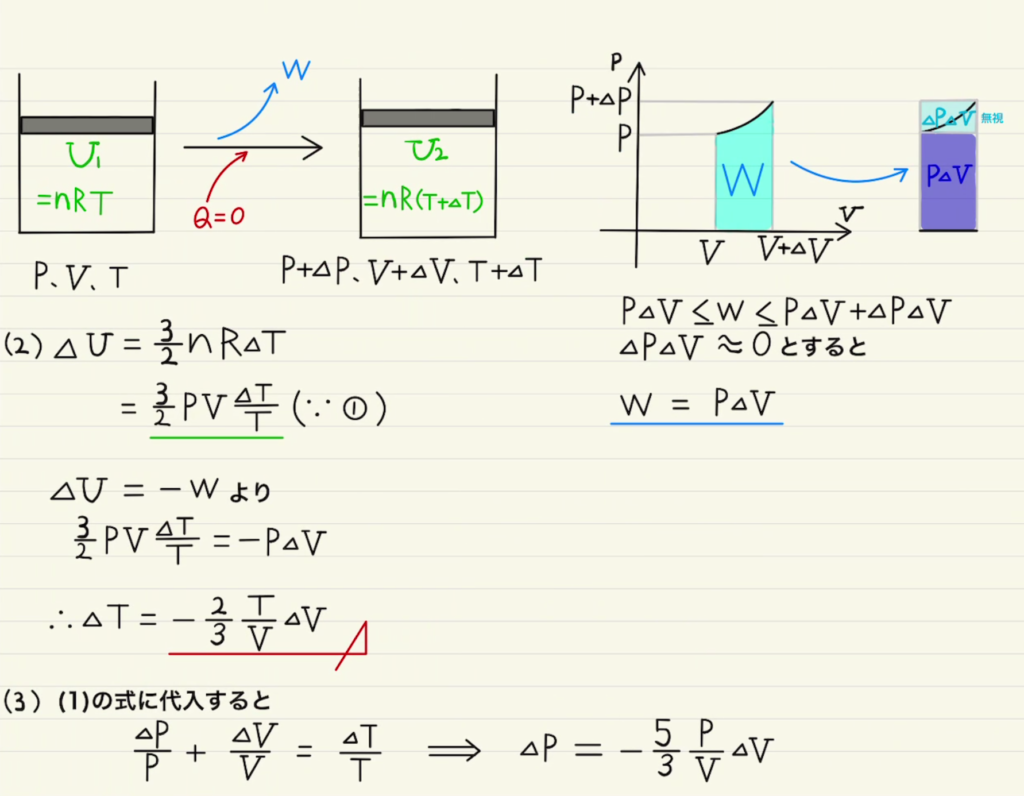
仕事に関しても$\int{PdV}$の面積も長方形として扱えます。
というか微小な仕事を$PdV$としているにすぎません。積分の足し合わせ前を考えているようなものですね。
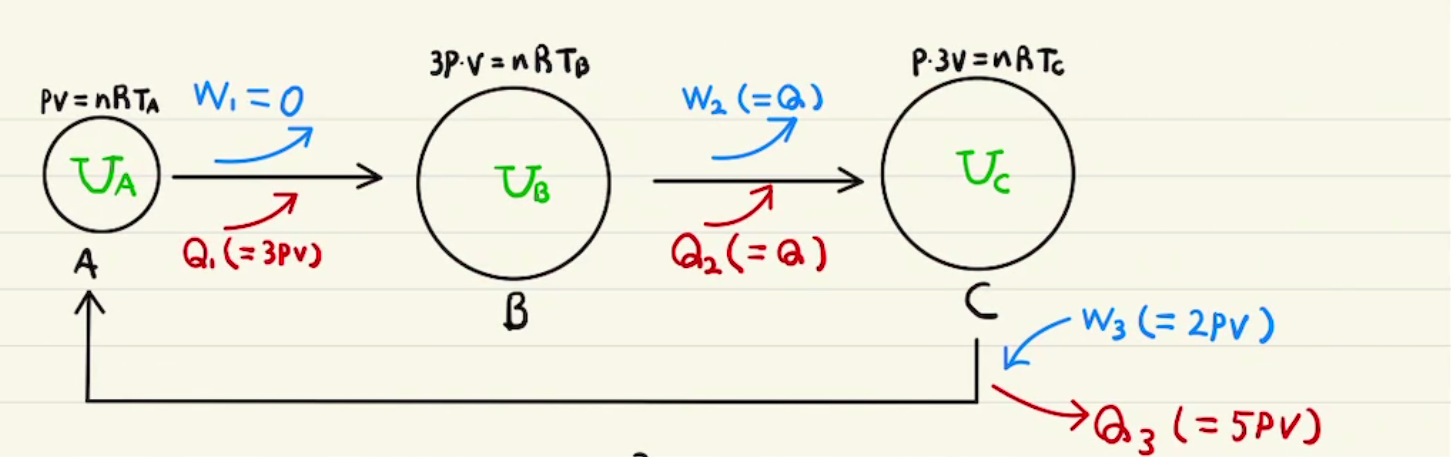
この結果からポアソンの法則が導けます。詳細は下の補足に記します。
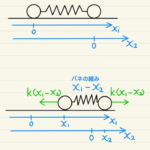
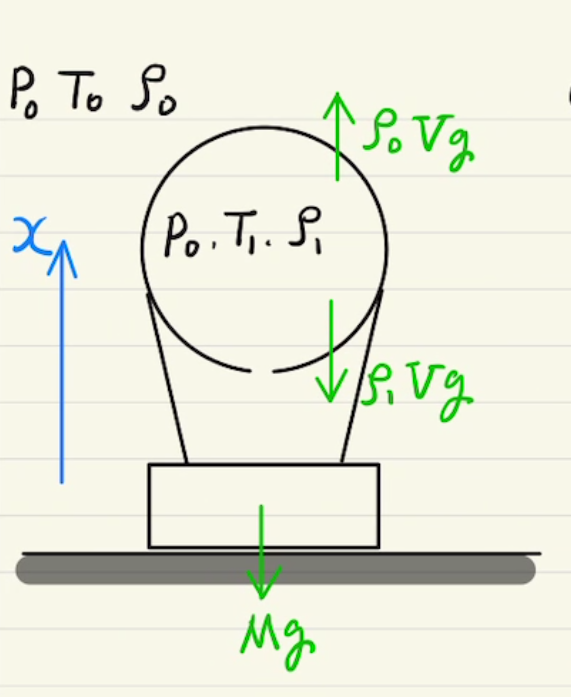
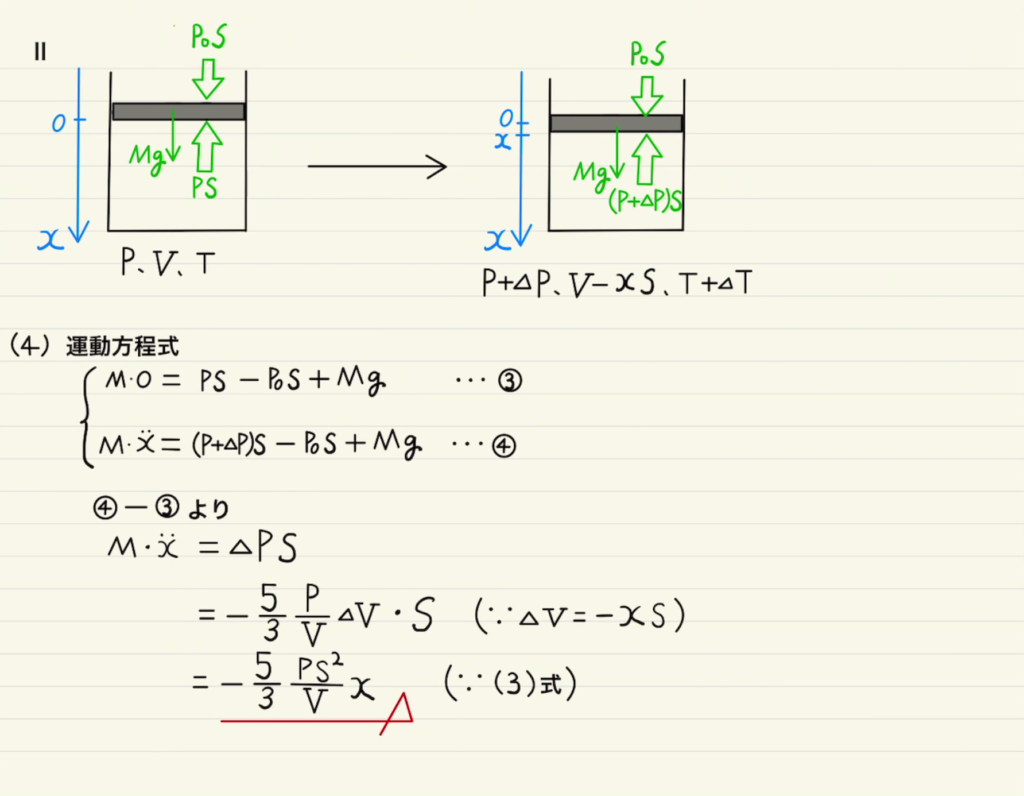
後半はその結果から気体の単振動をみるものです。
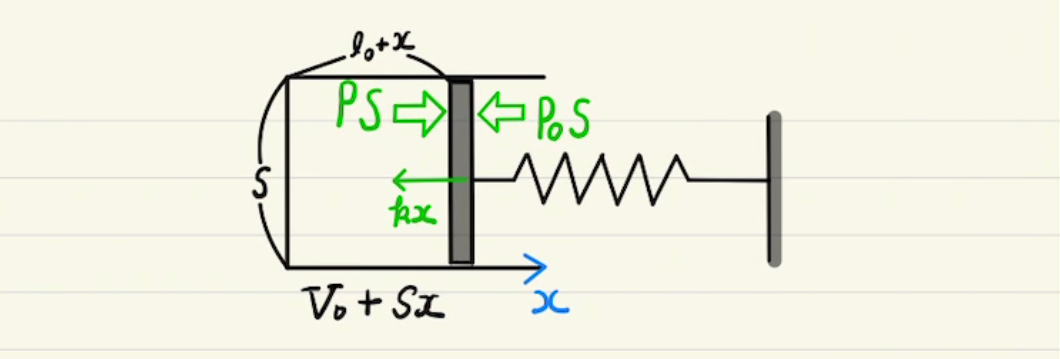
圧力等を記して、$m\ddot{x}=f$から微分方程式に持ち込みます。
速度は微分したら求まりますが、気を付けなければいけないのは、変数は時間$t$ではなく位置$x$ということです。
単振動の変形式、$(ωx)^2+v^2=一定$ を知っていれば予測がつきやすいでしょう。
力学的エネルギー保存を使ってもいいですが、保存するエネルギーが少しわかりにくいですね。
補足

Iの結果の$ΔV,ΔP$を微小量と考えて積分すると、ポアソンの公式
$$PV^γ=一定$$
が求まりました。今回は単原子分子のため、$γ=\frac{5}{3}$となっていますが、同様の方法で一般的な $γ=\frac{C_p}{C_v}$を求めることもできます。