真空中では光の速さは$c$は常に一定ですが、水やガラスのような媒質を通すと速度が遅くなります。
その速度が何分の1になるかを屈折率といいます。
媒質中での光の速さ$c_n$を式で表すと
$$c_n=\frac{c}{n}$$
となります。
屈折率は空気が1.0003、水で1.33、ガラスで1.45ほどです。
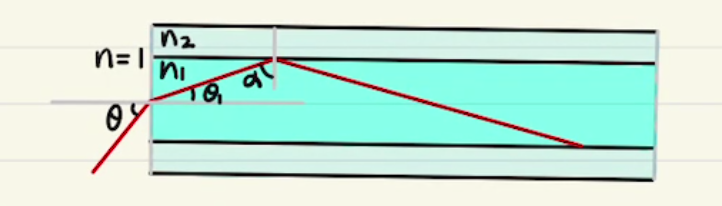
図のように屈折率$n_1$の媒質1から屈折率$n_2$の媒質2に光が入ったとすると次の屈折の式が成り立ちます。(スネルの法則)
$$n_1\sin{θ_1}= n_2\sin{θ_2} $$
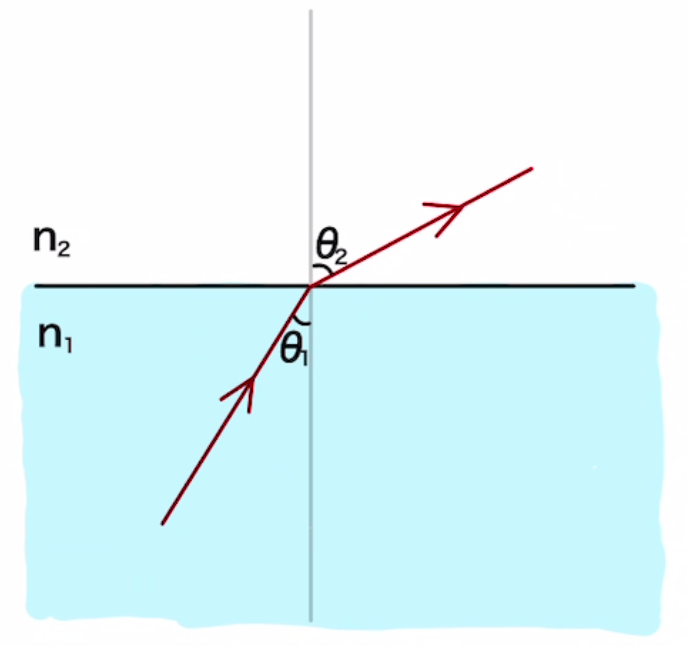
$n_1>n_2$のとき $θ_1$を次第に大きくしていくと $ \sin{θ_2} = \frac{n_1}{ n_2} \sin{θ_1} $が$1$になる角度が存在します。
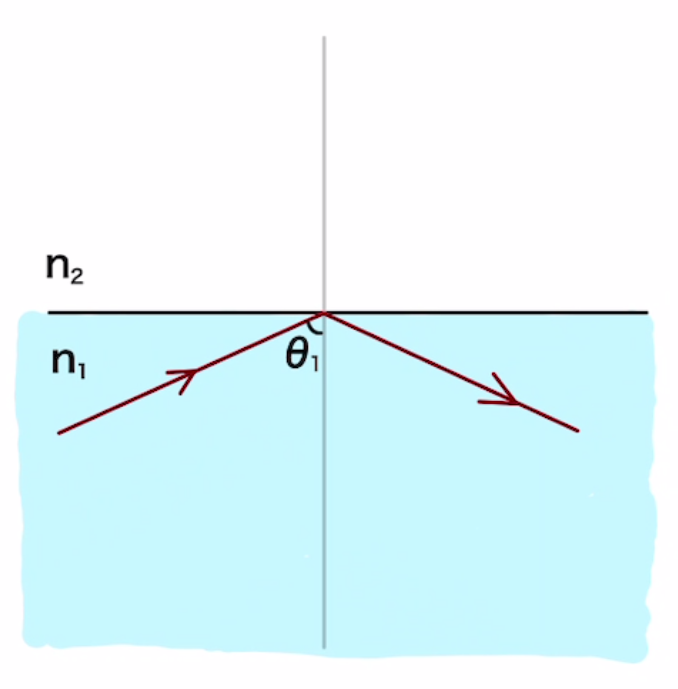
この角度より大きくなると屈折が起こらず全て光が反射します。これを全反射といいます。
補足
屈折率$n_1$の媒質での光の速度を$v_1$,波長を $λ_1$とすると
$ λ_1 = \frac{v_1}{f} = \frac{v}{n_1f} = \frac{λ}{n_1} $
つまり、速度、波長は屈折率に反比例します。 (そして$\sin{(屈折角)}$も屈折率に反比例します 。)
これを式にして書き直すと、
$$\frac{ n_{ {\color{green} 2} } }{n_ { {\color{blue} 1} } } = \frac{ v_ { {\color{blue} 1} } }{v_ { {\color{green} 2} } } = \frac{ λ_ { {\color{blue} 1} } }{λ_ { {\color{green} 2} } } = \frac{ \sin{θ_ { {\color{blue} 1} } } }{ \sin{θ_{ {\color{green} 2} } } } $$
と表すことができて $\frac{ n_{ {\color{green} 2} } }{n_ { {\color{blue} 1} } } $を相対屈折といい、$n_{1→2}$もしくは $n_{12}$と書くことがあります。
レンズ
レンズは屈折を利用して光を一カ所に集めるものを言います。
物はある点で光が反射して(もしくは自らが発光して)、それが目に届くことによって人は物を見ることができます。
一点から発散した光をレンズを使ってまた同じ場所に集め、そこから再び拡散することにより、像を作ります。像ができる場所にはあたかも物があるように見えます。
レンズは二回の屈折が起こりますが、厚さを無視して中央で一回光が折れ曲がるように書くのが一般的です。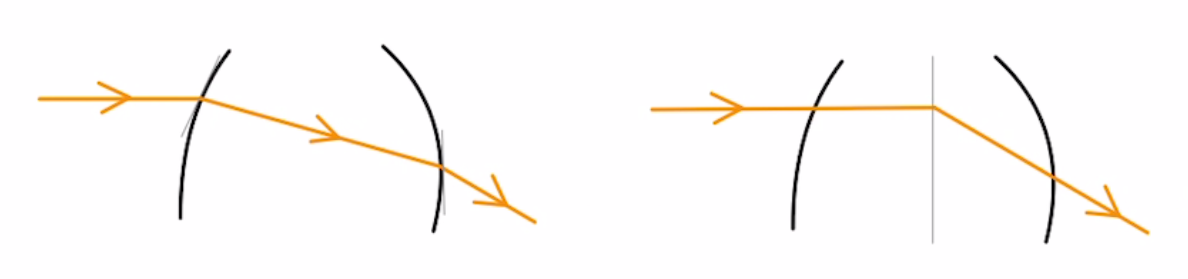
レンズは大まかに凸(とつ)レンズと凹(おう)レンズがあるのでそれぞれ見ていきましょう。
・凸レンズ
円孤の形で外に出っ張ったレンズを凸レンズといいます。
凸レンズは平行で入ってきた光がある一点に集まります。
このレンズからの距離を焦点距離といいます。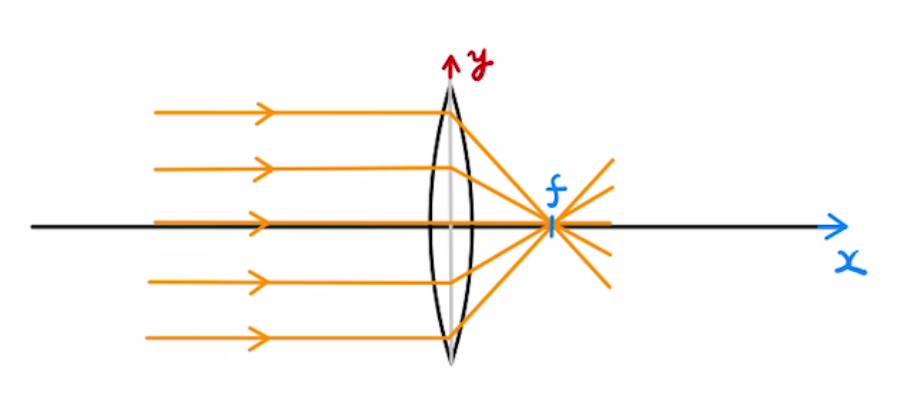
物が映るときはレンズに平行に入る光とレンズの中央を通る光を見ることで像ができる位置がわかります。
レンズから距離$a(>f)$だけ離れている、高さ$h$のろうそくの像を考えてみましょう。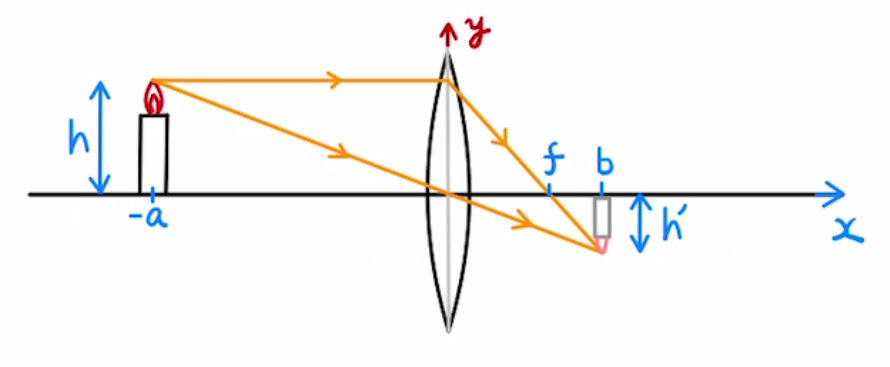
このとき平行で入った光は焦点を目指して進むため、式で表すと
$y=-\frac{h}{f}x+h$
となり、レンズの中央を通る光は入る光と出る光は平行であるため、式で表すと
$y=-\frac{h}{a}x$
となります。
これらの連立方程式を解くと、$x=\frac{fa}{a-f} ⇒ \frac{1}{a} + \frac{1}{x} =\frac{1}{f} $となり、
この点がレンズから像までの距離$b$のとき、であることから、レンズの公式
$$\frac{1}{a} + \frac{1}{b} =\frac{1}{f} $$
が成り立つことがわかります。
このとき$y=-\frac{f}{a-f}h$から、像の大きさ$h’$は
$$h’ = \frac{f}{a-f}h $$
となります。
・凹レンズ
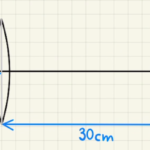
凹レンズは平行で入ってきた光が発散していきます。
この発散した光の直線が集まる点が焦点となります。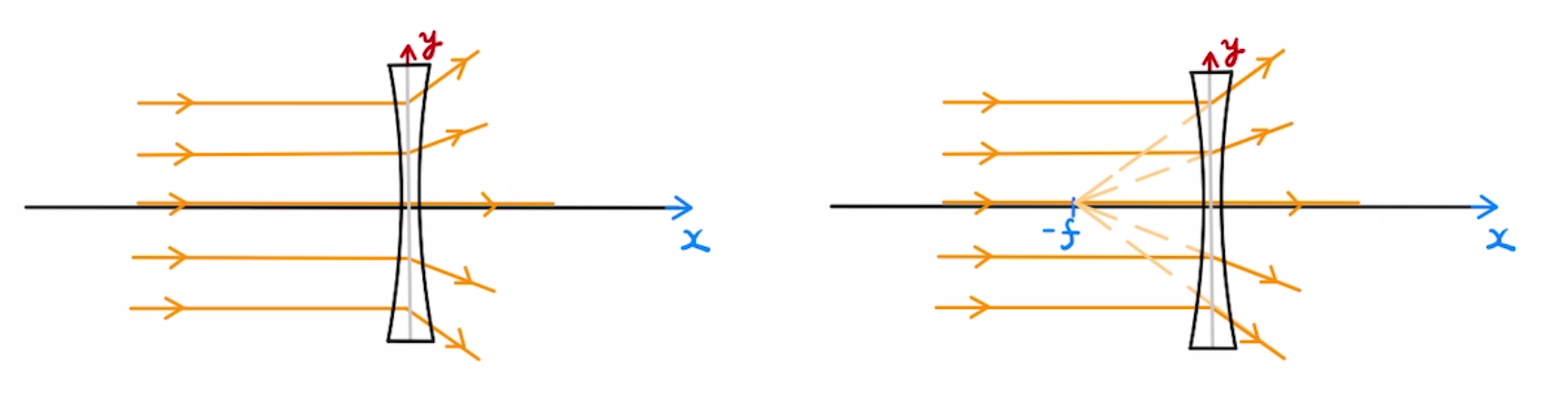
凸レンズ同様、ろうそくの像を考えていきます。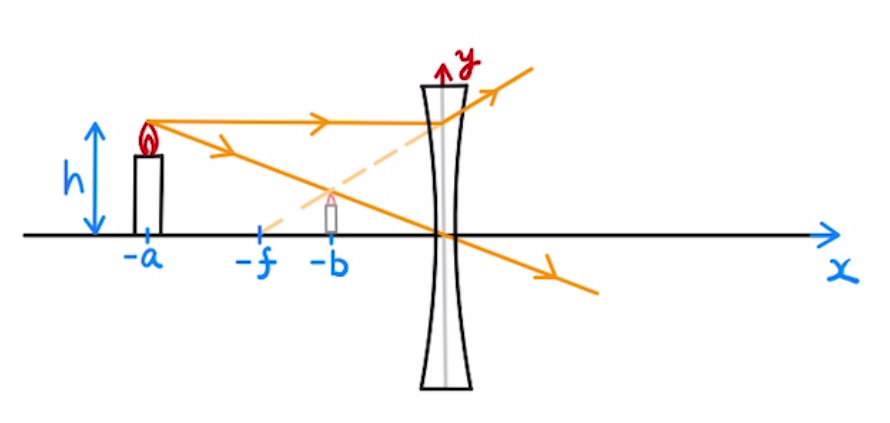
平行で入った光は、屈折し外に出ていきますが、その直線は焦点を通るため、式で表すと
$y=\frac{h}{f}x+h$
レンズの中央を通る光は入る光と出る光は平行であるため、式で表すと
$y=-\frac{h}{a}x$
となります。
これらの連立方程式を解くと、$x=-\frac{fa}{a+f} ⇒ \frac{1}{a} + \frac{1}{x} =-\frac{1}{f} $となり、
この点がレンズから像までの距離$x=-b$であることから、凹レンズ公式
$$\frac{1}{a}\, – \, \frac{1}{b} = -\frac{1}{f} $$
が成り立つことがわかります。
焦点距離$f$と像までの距離$b$がレンズの手前($x<0$)となるため、それをマイナスにしただけになります。
このとき$y=\frac{f}{a+f}h$から、像の大きさ$h’$は
$$h’ = \frac{f}{a+f}h $$
となります。
・統合した式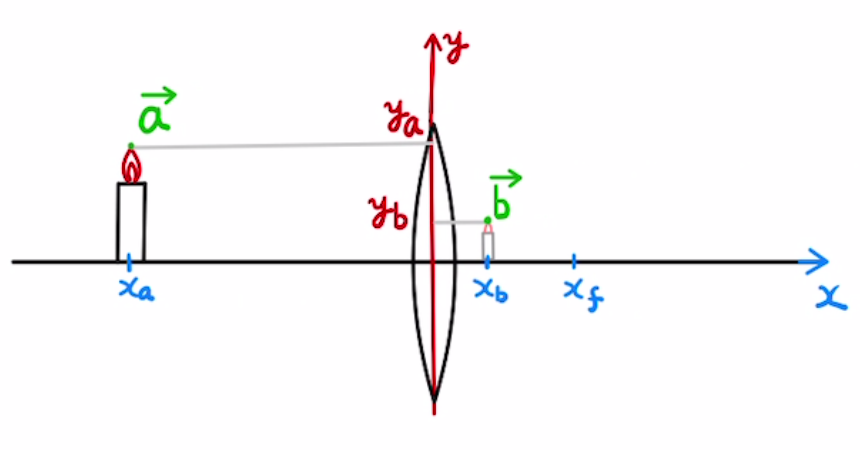
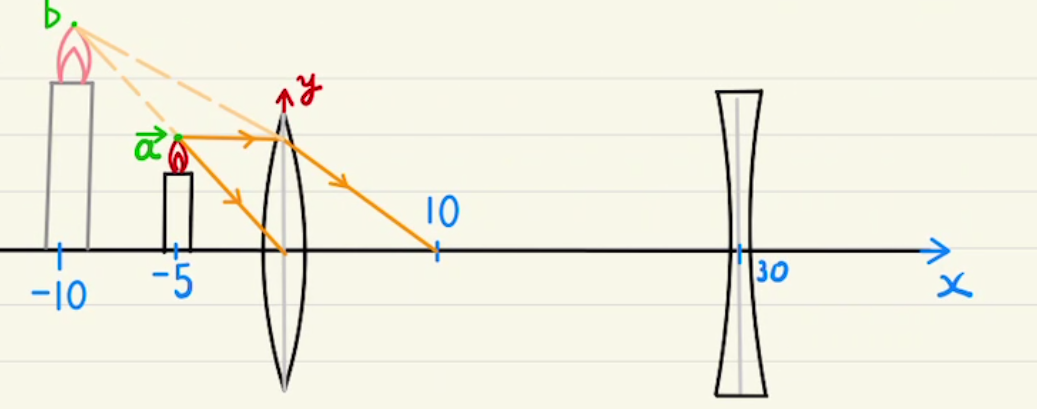
とある凹凸レンズの焦点の$x$座標を$f$としたとき、物体の位置が$\vec{a}$,物体の像の位置が $\vec{b}$ だったとします。
それぞれ以下のように表すとします。
$$ \vec{a} = \begin{bmatrix} x_a \\y_a \end{bmatrix},\; \vec{b} = \begin{bmatrix} x_b \\y_b \end{bmatrix} $$
このときレンズの式を一般化すると
$$-\frac{1}{x_a} + \frac{1}{x_b} = \frac{1}{f} ⇒ x_b = \frac{f}{x_a+f}x_a $$
となり、 物体の(先端の)$y$座標が$y_a$となるため、像の先端の$y$座標$y_b$は
$$y_b = \frac{f}{x_a+f}y_a $$
と表すことができます。
つまり、物体の位置$\vec{b}$は以下のように表せます。
$$ \vec{b} = \frac{f}{f+x_a} \vec{a} $$
この式は位置で表されるため、$x_a$だけマイナスですが他の変数は状況によりプラスにもマイナスにもなりえます。
凸レンズでは$f$は正、凹レンズでは $f$は負となります。当然ながら$ f+x_a=0$の時は像はできません。
$\vec{b}$の$x$成分が正なら実像、負なら虚像となります。
$\vec{b}$の$y$成分が正なら正立、負なら倒立となります。
また、$ \frac{f}{f+x_a}$の絶対値をレンズの倍率といいます。
※基本的に$x$座標は$x_a<0$となるように設定しています。$x_a>0$と設定することも可能ですが、その場合は焦点位置$f$の正負が逆になりますので注意しましょう。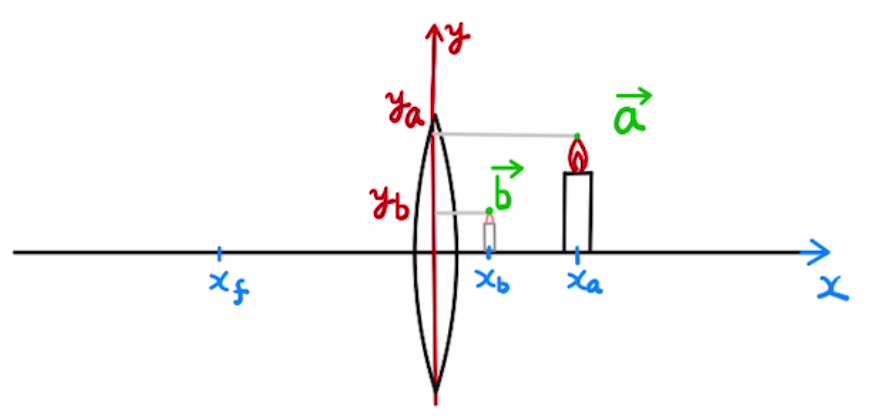
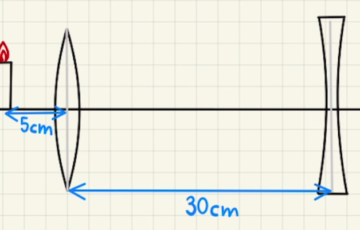
二つのレンズをくみあわせた場合も以下のように表せます。
$$ \vec{b_2} = \frac{f}{f+x_{a_1}} \vec{a_1} $$
詳しくは合成レンズをご覧ください。
まとめ
屈折率$n_1$の媒質1から屈折率$n_2$の媒質2に光が入ったとすると$$n_1\sin{θ_1}= n_2\sin{θ_2} $$
が成り立つ。
$n_1>n_2$のとき、$ \frac{n_1}{ n_2} \sin{θ_1} > 1$で全反射となる。
凸レンズや凹レンズは平行に入る光と、中央を通る光を作図すればわかる。
位置$\vec{a}$の物体は、以下の位置 $\vec{b}$に像を作る。
$$ \vec{b} = \frac{f}{f+x_a} \vec{a} $$