波動③’ 屈折と反射追記合成レンズ

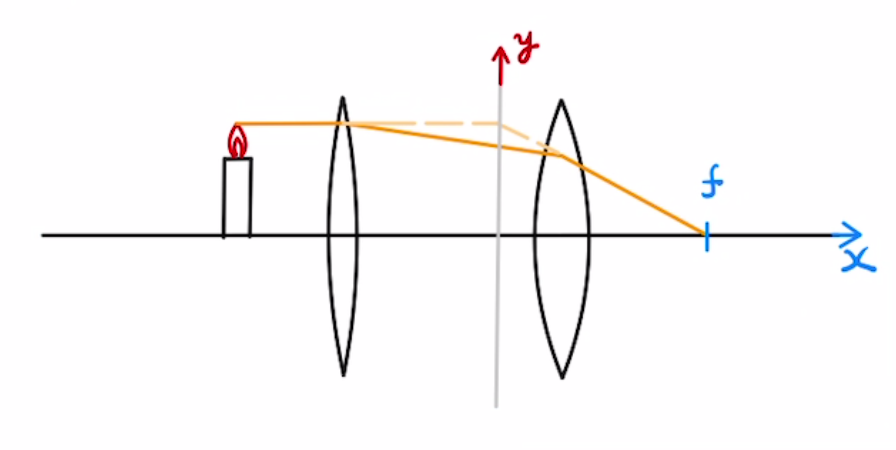
一般的に二枚のレンズの合成を考えることもできます。
焦点距離$f_1$のレンズ$L_1$と$f_2$のレンズ $L_2$ を距離$d$だけ離した場合、二つのレンズを一つのレンズのように扱え、焦点距離$f$は
$$ \frac{1}{f} = \frac{1}{f_1} + \frac{1}{f_2} \;- \frac{d}{f_1f_2} $$
となります。

この場合レンズの系の大きさが無視できないため、光の折れ曲がったとみなせる線(主点)は二つあります。

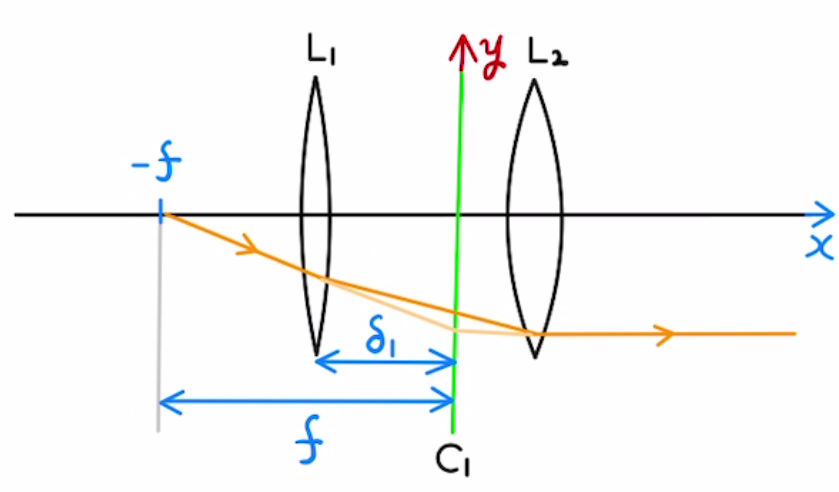
一つ目の主点$C_1$で折れ曲がる場合、ある一点から出た光が平行になって出ていきます。
レンズ$L_1$から主点$C_1$との距離 $δ_1$は以下のようになります。
$$ δ_1 = \frac{f}{f_2} d $$

二つ目の主点$C_2$で折れ曲がる場合、左から平行に光が入ってきたときで、ある一点で光が集まります。
レンズ$L_2$から主点$C_2$との距離 $δ_2$は以下のようになります。
$$ δ_2 = \frac{f}{f_1} d $$

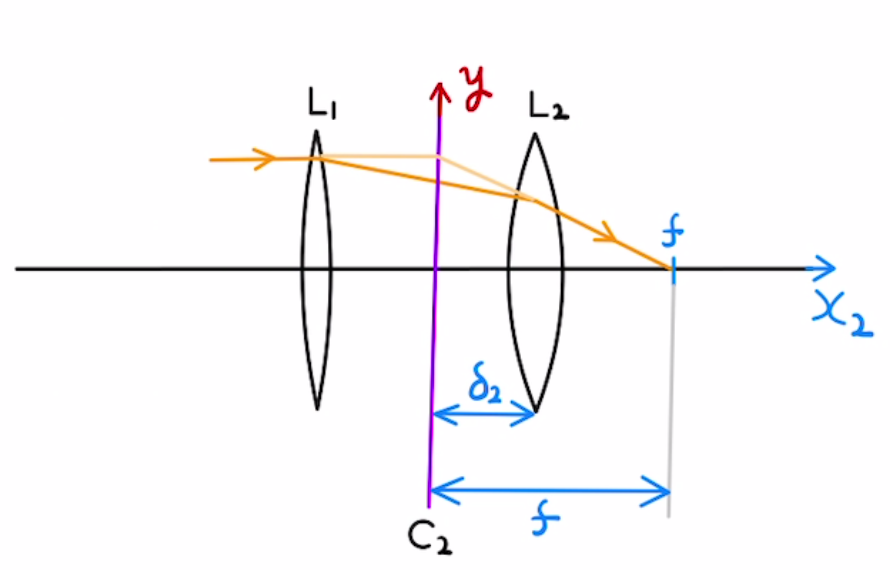
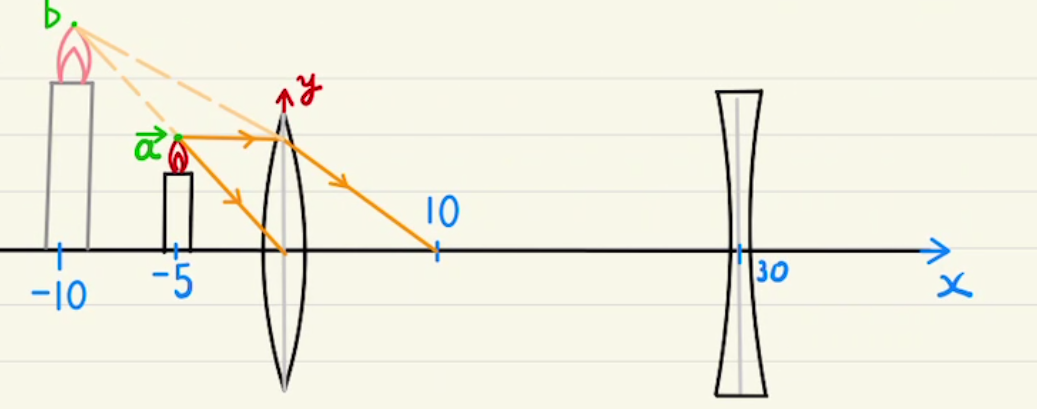
そこから図のように$a,b$を設定すると、以下のレンズの公式が成り立ちます。
$$\frac{1}{a}\, + \, \frac{1}{b} = \frac{1}{f} $$

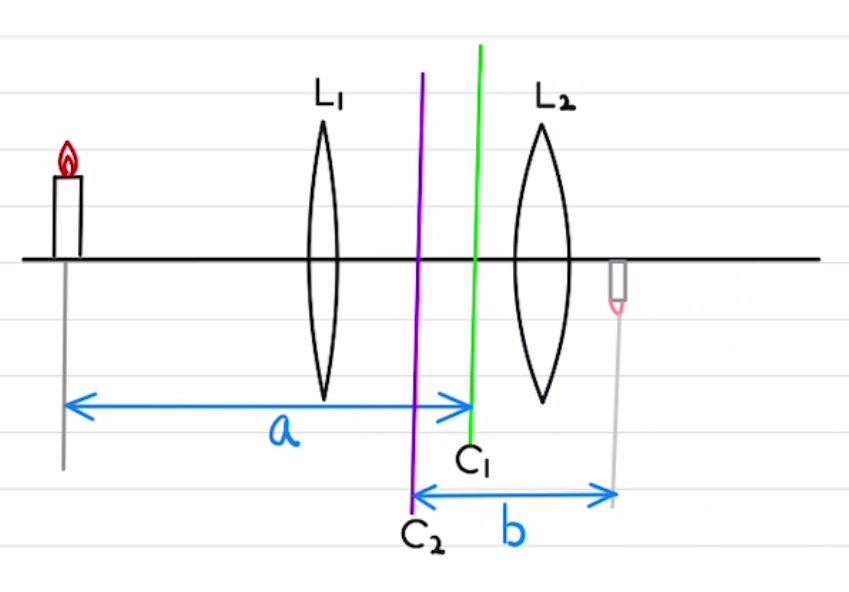
また、$y=y_a$にある物体が、$y=y_b$に像ができる場合、位置関係は以下のようになる。
$$\frac{ y_a }{a}\, + \, \frac{y_b}{b} = 0$$

・統合して、以下の式で表すことができます。
$$ \vec{b_2} = \frac{f}{f+x_{a_1}} \vec{a_1} $$

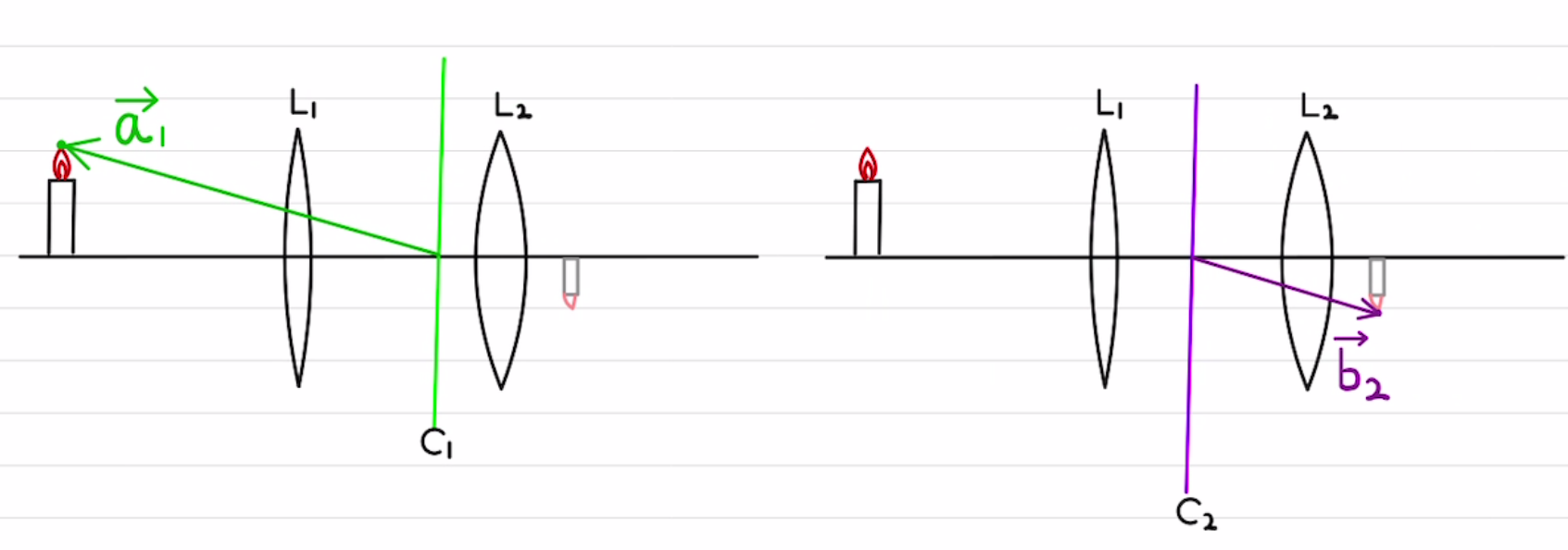
良問の風 84 解説のように、焦点10[cm]の凸レンズと焦点10[cm]の凹レンズを30cm離して置いた例を考えてみます。

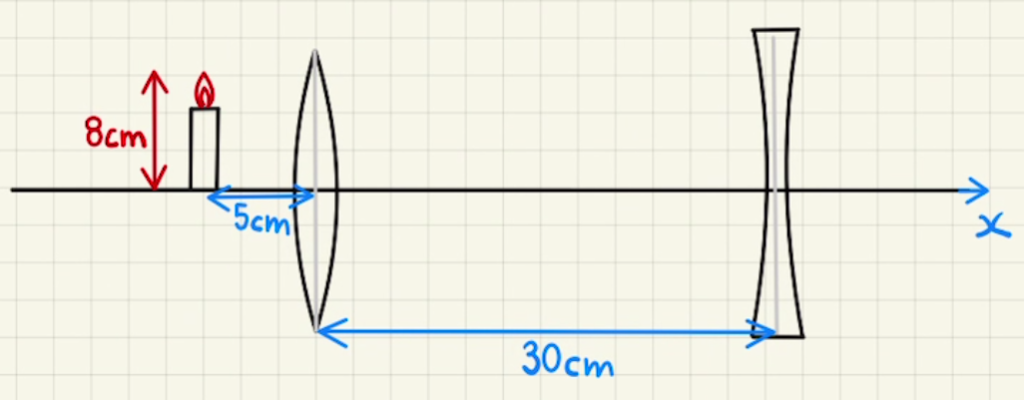
一つ目のレンズは焦点10[cm]の凸レンズとすれば、$f_1=10$
二う目のレンズは焦点10[cm]の凹レンズなので、$f_2=-10$
よって合成レンズの焦点$f$は
\begin{align}
\frac{1}{f} &= \frac{1}{f_1} + \frac{1}{f_2} – \frac{d}{f_1f_2}\\
&= \frac{1}{10} + \frac{1}{-10} – \frac{30}{-10×10}\\
&= -\frac{3}{10}\\
\end{align}
よって
$$f= \frac{10}{3} $$
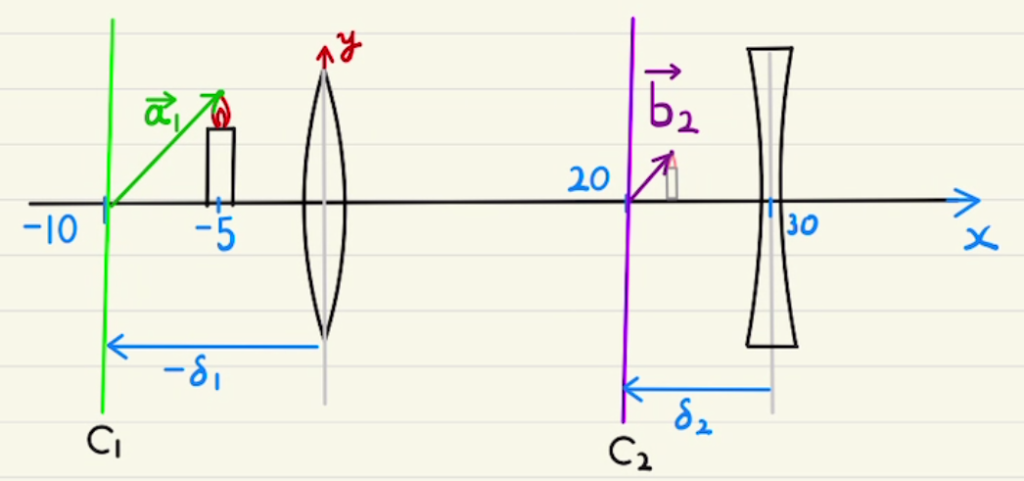
このことから、主点$C_1$との距離$δ_1$(右方向を正)と、主点$C_2$との距離 $δ_2$(左方向を正)とすると
$$δ_1= \frac{f}{f_2} d = \frac{10/3}{-10}×30 =-10$$
$$δ_2= \frac{f}{f_1} d = \frac{10/3}{10}×30 =10$$
となります。

そのことから物体の位置は
$$ \vec{a_1} = \begin{bmatrix} -5 – δ_1 \\8 \end{bmatrix} = \begin{bmatrix} 5 \\8 \end{bmatrix} $$
となり、レンズの式から
$$ \vec{b_2} = \frac{f}{f+x_{a_1}} \vec{a_1} = \frac{ \frac{10}{3}}{ \frac{10}{3} + 5} \begin{bmatrix} 5 \\8 \end{bmatrix} = \begin{bmatrix} 2 \\ \frac{16}{5} \end{bmatrix} $$
$L_2$から見ると$2 – δ_2 = -8$の位置にあることから、 $L_2$の前方(左)$8$[cm]の位置に$\frac{16}{5}$の大きさで正立しているのが見えます。