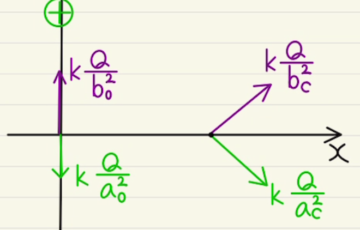
電気にはプラスとマイナスがあります。
プラスの元となるのが陽子、マイナスの元となるのが電子となります。
プラス同士の電気は引き離そうとする力が働きます。(斥力)
万有引力とは逆ですね。
その力の大きさは
$$f=k\frac{q_1q_2}{r^2}$$
$k$:クーロン定数 $q_1, q_2$:電荷の大きさ、$r$:二つの距離
となります。
逆にプラスとマイナスの場合はひきつけあおうとします。(引力)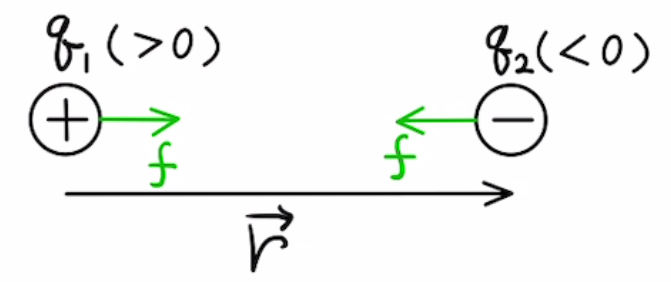
上の斥力と引力を統合し、方向も含めたベクトルの形式で以下のように書くこともできます。
$$\vec{f}=k\frac{q_1q_2}{r^2}×\frac{\vec{r}}{r}$$
$ \vec{r} $ :$q_2$の位置ベクトル $ \vec{f} $ :$q_2$にかかる力
この場合、$ q_1,q_2 $はプラス電荷なら正、マイナス電荷なら負になります。
万有引力では定数はおよそ$G≈6.7×10^{-11}$だったのに対し、クーロン定数は$k≈9.0×10^9$となるため、非常に大きい力となっています。
静電気の位置エネルギー
静電気も万有引力と同様に位置エネルギーが存在します。
プラス同士の場合は、より引き離そうとする力なので近づけるために仕事をする必要があります。
つまり近いほど位置エネルギーが大きく、遠いほどエネルギーが低い状態になります。
無限遠点を基準として
$$ U = \int_∞^r{ k\frac{ q_1q_2 }{x^2} }dx = k\frac{ q_1q_2 }{r} $$
これが静電気のエネルギーとなります。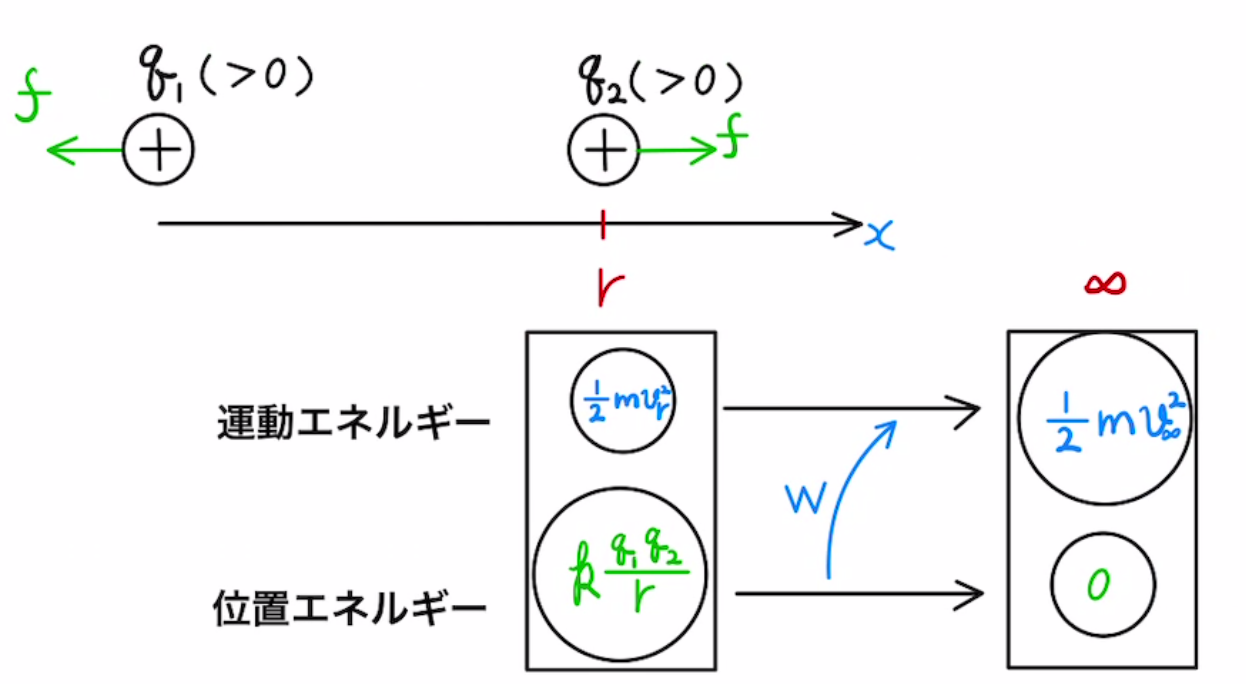
電場と電位
電荷の影響で、1[C](クーロン)あたりにかかる静電気力を電場、
1[C]あたりに位置エネルギーを電位と言います。
・電場
電場は1[C]あたりにかかる静電気力を表します。
$q_1$の電荷から$\vec{r}$だけ離れているとき、電場は以下のように表せます。
$$\vec{E}=k\frac{q_1}{r^2}×\frac{\vec{r}}{r}$$
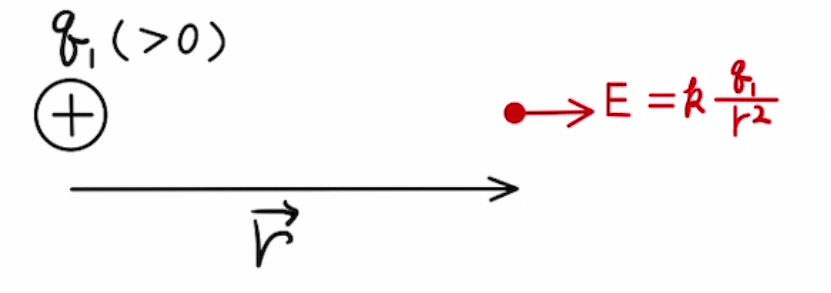
複数の電荷の影響を受ける場合は力と同様、ベクトルを足し算することによって電場が求まります。
もし、電場$\vec{E}$に$q_2$の電荷を置くと、かかる静電気力$\vec{f}$は以下のようになります。
$$\vec{f}=q_2\vec{E}$$
・電位
電位は1[C]あたりの位置エネルギーに相当し、以下のように定義されます。
$$ V = k\frac{ q_1}{r} $$
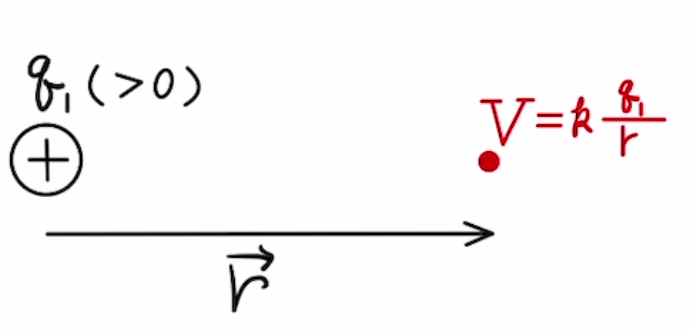
電位は1[C]あたりの位置エネルギーに相当するため、ベクトルではないことに注意しましょう。
こちらも複数の電荷の影響がある場合は足し合わせで求めることができます。
もし、電位$V$の所に$q_2$の電荷を置くと、位置エネルギー$U$は以下のようになります。
$$U=q_2V$$
力学でいえば、重力(電場)に逆らって動かすと位置エネルギー(電位)が上昇するイメージですね。
一様な電場と重力場
静電気は目に見ることができないので少しイメージはつきづらいと思います。
なので、今回は力学での重力と比較を行っていきます。
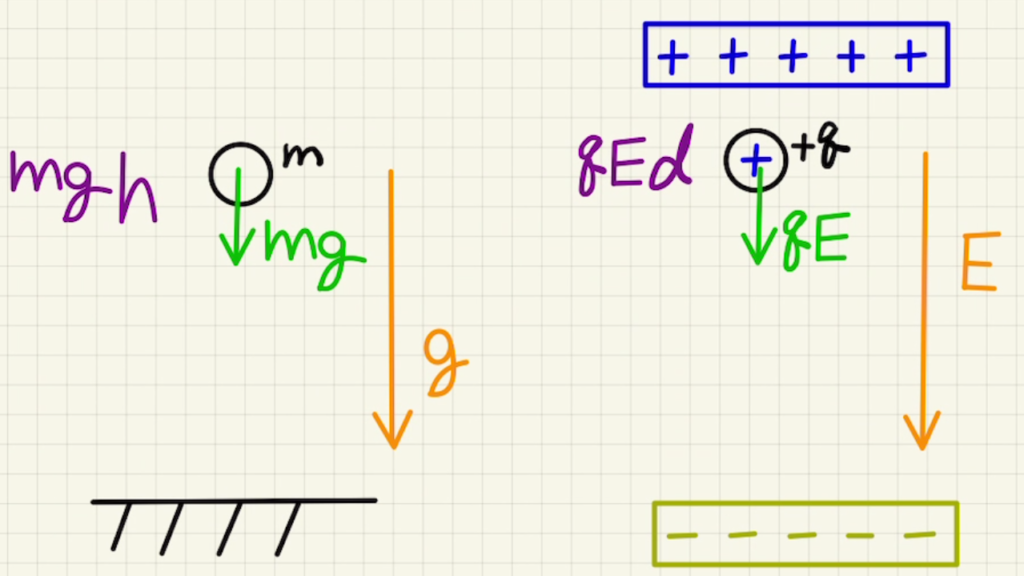
上の図のように質量$m$のある物体が重力加速度$g$の重力場がある場所を考えます。
そこでは地面に向かって重力$mg$がかかります。
地面から重力に差からって高さ$h$だけ持ち上げることで、位置エネルギーを$mgh$だけ手に入れます。
静電気力ではどうでしょう。
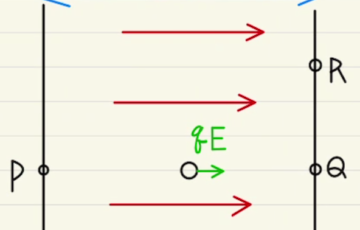
上から下に向かって一様な電場$E$を発生させます。(コンデンサーの内部のイメージです。)
同様に電荷$+q$あると、静電気力$qE$がかかります。
その力に逆らって距離$d$だけ上に移動させると静電エネルギーを$qEd$だけ手にいれます。
質量$m$⇒電荷$q$
重力加速度$g$⇒電場$E$
重力$mg$⇒静電気力$qE$
位置エネルギー$mgh$⇒静電エネルギー$qEd$
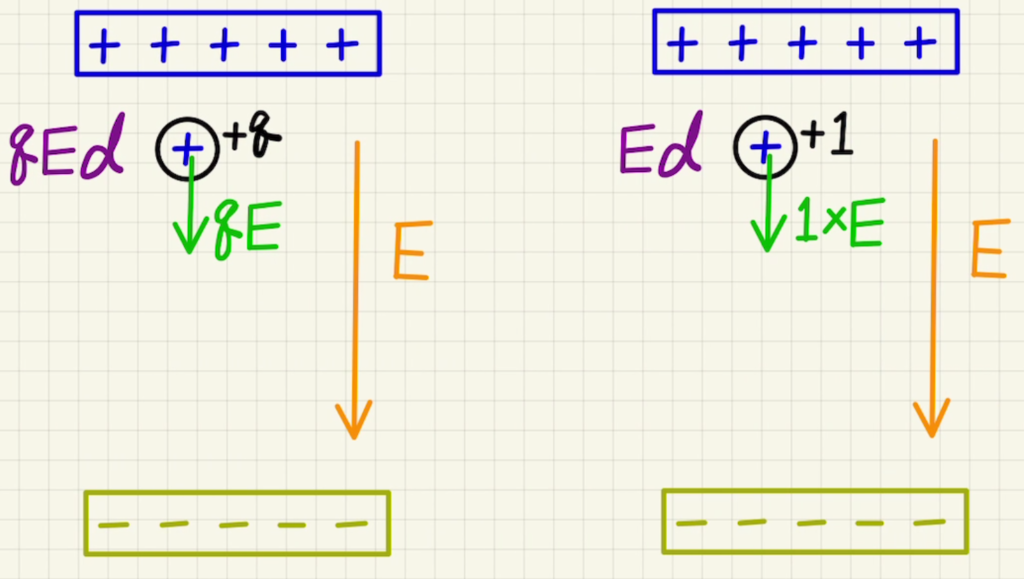
$1[C]$当たりで考えれば電位も考えることができます。
1kg当たりの位置エネルギー$gh$⇒電位$Ed$
電場$E$に逆らう方向に$d$だけ進めば、電位が$Ed$だけ上昇します。
電場に逆らう方向に移動すると電位が上がるのを常に意識しましょう。
まとめ
静電気力は以下の式で表わされる。
$$\vec{f}=k\frac{q_1q_2}{r^2}×\frac{\vec{r}}{r}$$
また静電気力の位置エネルギーは以下のよう。
$$ U= k\frac{ q_1q_2 }{r} $$
電場は1[C]あたりの静電気力で
$$\vec{E}=k\frac{q_1}{r^2}×\frac{\vec{r}}{r}$$
電位は1[C]あたりの位置エネルギーで
$$ V= k\frac{ q_1}{r} $$
となる。
いずれも、複数の電荷がある場合はそれらを足し合わせることで求まる。