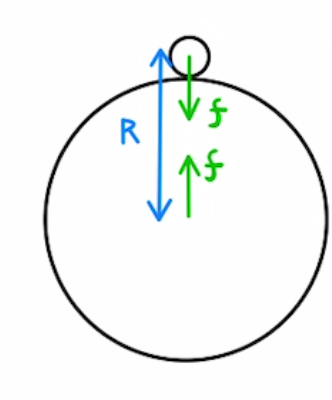
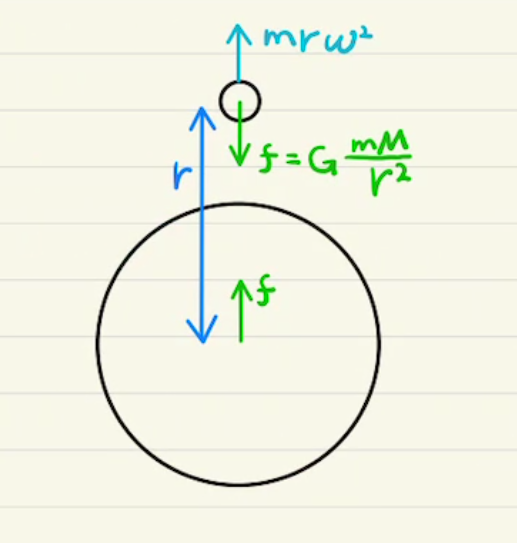
全ての質量と質量はひきつけあっています。これを万有引力と言います。
これはあまりにも小さな力なため、私たちは身近に感じることはありません。
しかし、質量が非常に大きい場合は例外です。
地球という大きな質量にひきつけられることによって下に引っ張られるように感じます。
質量同士がひきつけある引力の大きさは下のようになります。
$$f=G\frac{mM}{r^2}$$
$G$:定数、$m$:物体1の質量、$M$:物体2の質量、$r$:二物体の距離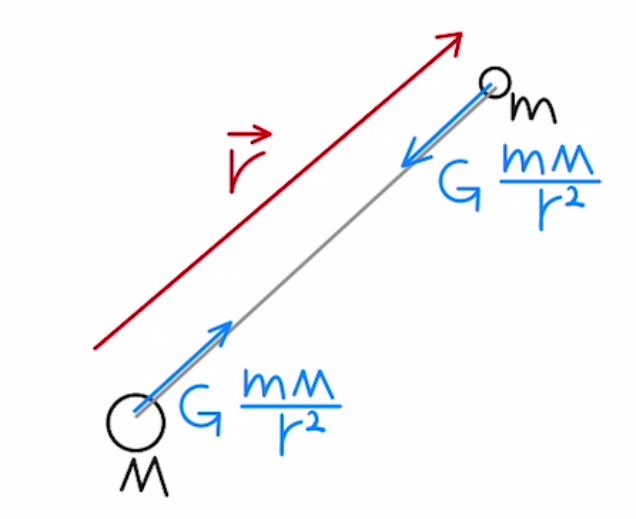
引力の大きさは、それぞれの質量に比例し、距離の二乗に反比例する形になります。
引力を受ける方向はもう一つの物体がある方向、つまり物体の位置ベクトルの反対方向となるため、ベクトル表記でこう書くこともあります。
$$\vec{f}=-G\frac{mM}{r^2}× \frac{\vec{r}}{r} $$
地球での重力を考える場合、人が感じる万有引力は以下のようになります。
$f=G\frac{mM}{R^2}= m×\frac{GM}{R^2} $
$G$:定数、$m$:人の質量、$M$:地球の質量、$r$:地球の半径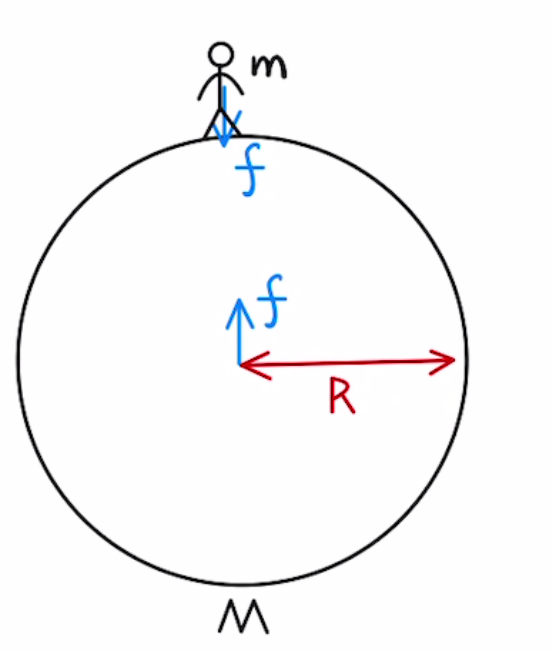
地上では$ \frac{GM}{R^2} $ がほぼ一定なので重力加速度$g$として$f=mg$の力がかかります。
万有引力の位置エネルギー
万有引力は力であるため、当然物を動かせば仕事をします。そして、エネルギーとして扱うこともあります。
これも位置によってエネルギーが決まるため、位置エネルギー(もしくはポテンシャルエネルギー)と言います。
万有引力は引く力であるため、より物体を近づけることによって仕事をします。
つまり離れている状態では位置エネルギーが高く、近づくことによって位置エネルギーが運動エネルギーに変換された、ということができます。
エネルギーは相対的なものなのでどこをエネルギーの基準に置いてもいいのですが、$r=0$をエネルギー$0$の点として設定すると $r=0$では力は∞であり、エネルギーは常に∞になってしまうため適切ではありません。
そのため今回は無限遠点、つまりは $r=∞$でエネルギーが$0$になると設定します。
離れているほどエネルギーが高いことを考慮すると、エネルギーの値はマイナスとなります。(あくまでエネルギーは相対的なものなので問題ありません。)
下図のような$r$軸だけの1次元の座標を考えます。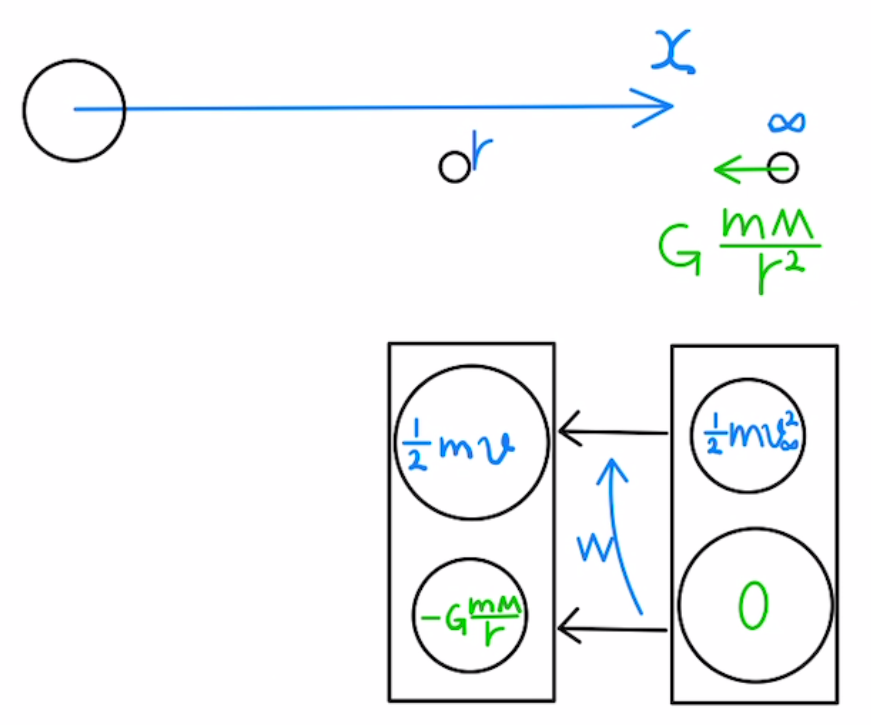
このときかかる力は$-G\frac{mM}{x^2} $から、力の持つエネルギーの定義に従い、
$$ U(r) = -\int_∞^r{ – G\frac{mM}{x^2} }dx = -\left[ G\frac{mM}{x} \right] _∞^r = -G\frac{mM}{r} $$
ケプラーの法則
万有引力から天体運動は三つのケプラーの法則にしたがうことが導けます。
・第一法則
二つの天体は万有引力によって楕円運動をする。
・第二法則
面積速度は一定である。
面積速度は $\dot{S} = \frac{1}{2}|\vec{r}×\vec{v}|$ で定義され、 $\frac{1}{2}rv\cos{θ}$とも書けます。
・第三法則
楕円運動の長軸半径を$a$、周期を$T$とすると、
$$\frac{T^2}{a^3}=一定$$

これらの第一法則と第三法則に関しては、証明をするために極座標と二次曲線(数Ⅲの範囲)となるため、無理に見なくてもいいでしょう。
(一応、証明は非常に難しいです。ここの補足で説明していますので、興味のある方だけ確認ください。)
ただし、 円運動の時の第三法則の証明はよく出題されるため、知っておくべきです。
第二法則の導出に関わる問題はたまに出題されるため、確認しておくことをお勧めします。(例:2020 東大 大問1)
こちらはベクトルの外積だけ知っていれば導出は可能ですし、全体像を把握するのにも役立ちます。
面積速度一定(ケプラーの第二法則)
今二つの天体を考えるときに、片方の質量を$m$、もう片方を$M$として、m<<Mのときに軽いほう(質量$m$)を見ていきます。
角運動量は以下のように定義されます。
$$\vec{L} = \vec{r} × \vec{p}$$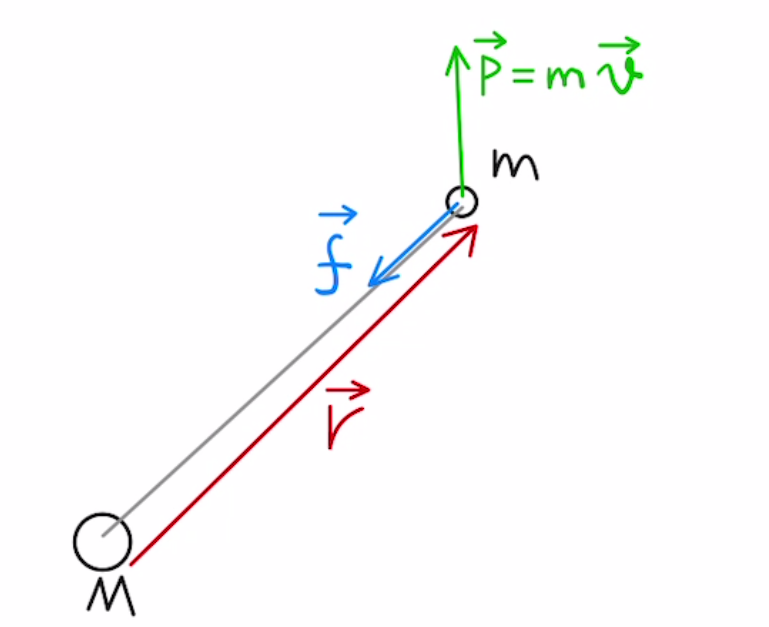
$\vec{p}$は運動量$m\vec{v}$であり、$\vec{L} = m(\vec{r} × \vec{v})$なので
これを時間で微分すると
$\frac{d\vec{L}}{dt} =m( \frac{d\vec{r}}{dt} × \vec{v} + \vec{r} × \frac{d\vec{v}}{dt} ) $
$ = m( \vec{v} × \vec{v} + \vec{r} × \vec{a} ) $
ここで$ \vec{v} × \vec{v} = 0$から
$ \frac{d\vec{L}}{dt} = \vec{r} × m\vec{a} $
また、$ \vec{f} = m\vec{a}$ なので、
$$\frac{d\vec{L}}{dt} = \vec{r} × \vec{f} $$
これはモーメントの定義に相当します。
つまり、運動量$ m\vec{v} $を時間微分したら$ \vec{f} $になるように、 角運動量$ \vec{r} × m\vec{v} $を時間微分したら$ \vec{N} $ となります。
今回は$ \vec{r} $と $ \vec{f} $は平行なので、 $ \frac{d\vec{L}}{dt} = \vec{0} $となります。
このことから、角運動量は時間で変化せず一定であり
$$ \vec{L} = m\vec{r} × \vec{v} = 一定$$となります。
ここで面積速度は
$$\dot{S} = \frac{1}{2}|\vec{r}×\vec{v}|$$
と表されるためこちらも一定となることがわかります。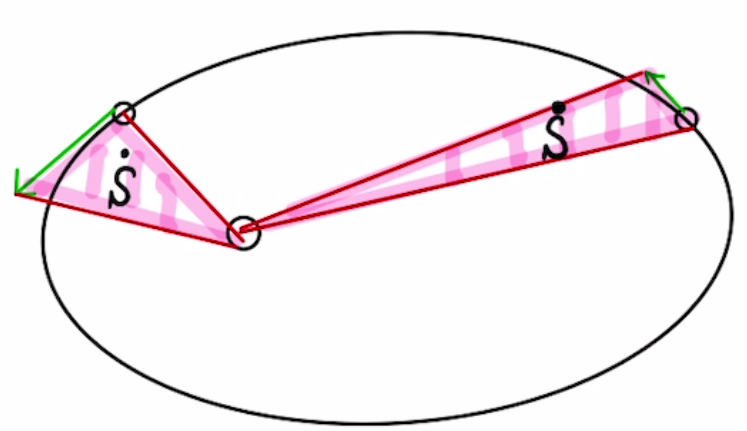
$x$方向、$y$方向の要素に分解して考えることもできます。
位置ベクトル$ \vec{r} $と速度ベクトル $ \vec{v} $ を
$$ \vec{r} = \begin{bmatrix} x \\ y \end{bmatrix} , \vec{v} = \begin{bmatrix} v_x \\ v_y \end{bmatrix} $$
とおけるため、
$$ \vec{r}×\vec{v}= \begin{bmatrix} x \\ y \\ 0 \end{bmatrix} × \begin{bmatrix} v_x \\ v_y \\0 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\xv_y-yv_x \end{bmatrix} $$
つまり、
$$\dot{S} = \frac{1}{2}( xv_y-yv_x ) =一定$$
となります。
さらに時間で微分すると
$\frac{d}{dt}(\vec{r}×\vec{v}) = \frac{d \vec{r} }{dt} ×\vec{v}+ \vec{r}× \frac{d\vec{v} }{dt} = \vec{v} ×\vec{v}+ \vec{r}× \vec{a} = \vec{r}× \vec{a} $
から、$$ \vec{a} = \begin{bmatrix} a_x \\ a_y \\ 0 \end{bmatrix} $$とすれば
$$\ddot{S} = \frac{1}{2}( xa_y-ya_x ) =0$$
と表すこともあります。
円運動の時のケプラー第三法則
万有引力が遠心力と釣り合うため、
$$ G\frac{mM}{R^2} = m\frac{v^2}{r}$$
よって$$r=\frac{GM}{v^2} ① $$
また、一周$ 2πr $の距離を速度$v$で回るため、周期は$T=\frac{2πr}{v}$となり、
$$ v=\frac{2πr}{T} ② $$
この①、②の二式から、
$$r=\frac{GM}{v^2} = \frac{GMT^2}{4π^2r^2} $$
よって
$$\frac{T^2}{r^3} = \frac {4π^2} {GM}=一定 $$
となります。
つまり周期の二乗が半径の3乗に比例することになります。
まとめ
二物体は万有引力でひきつけあい、その力の大きさは
$$f=G\frac{mM}{r^2}$$
となる。
そこから位置エネルギーも定義できて、無限遠点をエネルギー0とすると
$$U=-G\frac{mM}{r}$$
と常にマイナスになる。
またケプラーの三つの法則により、
・第一法則
二つの天体は万有引力によって楕円運動をする。
・第二法則()
面積速度は $\dot{S} = \frac{1}{2}|\vec{r}×\vec{v}|=一定$
・第三法則
$$\frac{T^2}{a^3}=一定$$
$a$: 楕円運動の長軸半径 、$T$:周期
天体の動きを見るときはエネルギー保存則と面積速度一定の式を連立することが多いです。