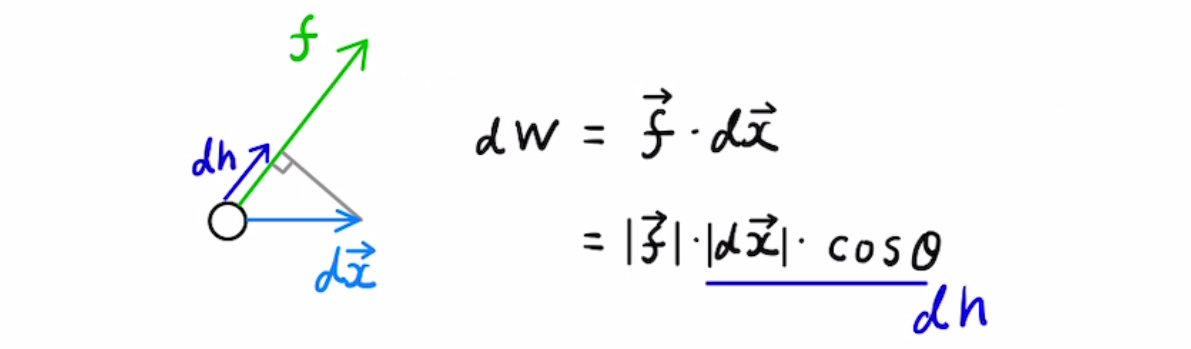力学的エネルギーとは力を及ぼすものがそれぞれエネルギーを持っていると考え、それを足し合わせたものは全て等しいものという自然法則です。
重力によるエネルギーは$mgh$(位置エネルギー)、バネによるエネルギーは $\frac{1}{2}kd^2$ (弾性エネルギー)。
力を及ぼすもの以外でもエネルギーとみなすものが一つあります。それは物体の速度です。
これは運動エネルギーとよばれ、$\frac{1}{2}mv^2$となります。
これらの合計は等しくあり続けます。
このまま公式を丸暗記してしまってもいいのですが、そもそもなぜそんなことがなりたつのでしょう?
これは実は運動方程式
$$ ma = f $$
から導かれたものです。
これから説明する導出は数Ⅲの微積分を含むため、習ってない人は軽く流しといてください。
加速度$a$は速度を時間微分したものであるため、 $\dot{v}$と表せます。(・は時間微分の意味)
よって運動方程式の両辺に速度をかけると
$$ mv\dot{v} = fv $$
となり、この両辺をある時刻$0$から時刻$t_1$まで時間積分すると
$$ \left[{\frac{1}{2}mv^2}\right]_{t=0}^{t=t_1} = \int_0^{t_1}{fv}dt $$
となります。(これは逆に合成関数として微分してみるとわかります。)
そして$ vdt = \frac{dx}{dt}×dt = dx$となるため、
$x=0$から$x=h$に移動したとすると下の式のように書けます。
$$ \left[{\frac{1}{2}mv^2}\right]_{x=0}^{x=h} = \int_0^h{f}dx $$
これが力学的エネルギー保存の式です。
左辺は変化量のため、わかりやすさのために下のように書くこともあります。
$$ Δ\left[{\frac{1}{2}mv^2}\right] = \int_0^h{f}dx $$
$ \frac{1}{2}mv^2 $が運動エネルギーの式、$ \int{f}dx $が力が物体に与えるエネルギーとなり、これを仕事とよびます。
これはある点($x=0$)からある点($x=h$)までに力がした仕事の分(与えたエネルギー分)、運動エネルギーが増えることを示しています。
位置エネルギー
一つ重力で例を考えてみましょう。
地上では質量$m$の物体は$mg$の力を受けます。
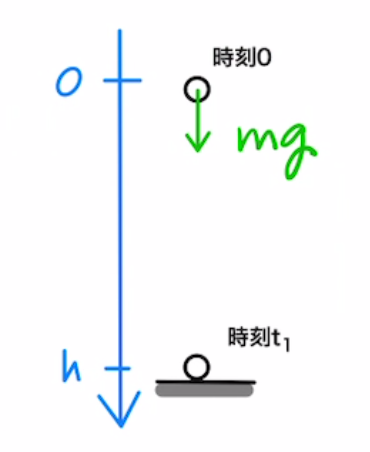
$h$の高さから落として地上まで落下したとき、$f$が常に$mg$で一定なことから、 重力のする仕事は $mg×h$となる。(グラフの面積の部分)
つまり「重力は物体に$mgh$の仕事をした」ということになります。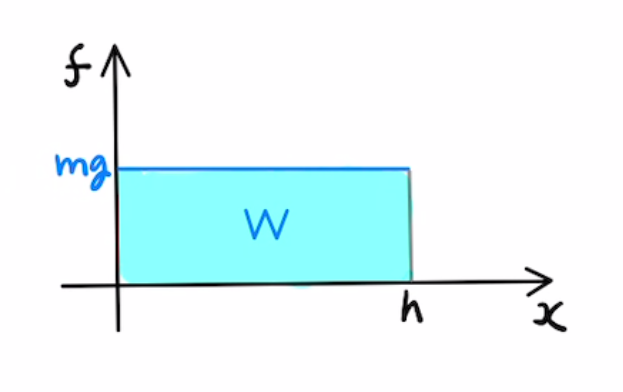
これは別の説明の仕方もできるはずです。
重力は元々エネルギーを持っていたが、「重力の持つエネルギーが運動エネルギーに移された」ということです。
重力の持つエネルギーを地上では$0$だとすると、地上から高さ$h$にある場合は$mgh$ということができます。
この重力の持つエネルギーを地球では高さに比例するため、位置エネルギーといいます。(ポテンシャルエネルギーともいいます。)
重力しか力を受けない環境(もっと厳密に言えば外とエネルギーのやり取りがない環境)なら $ 運動エネルギー\frac{1}{2}mv^2+位置エネルギーmgh = 一定$というわけです。 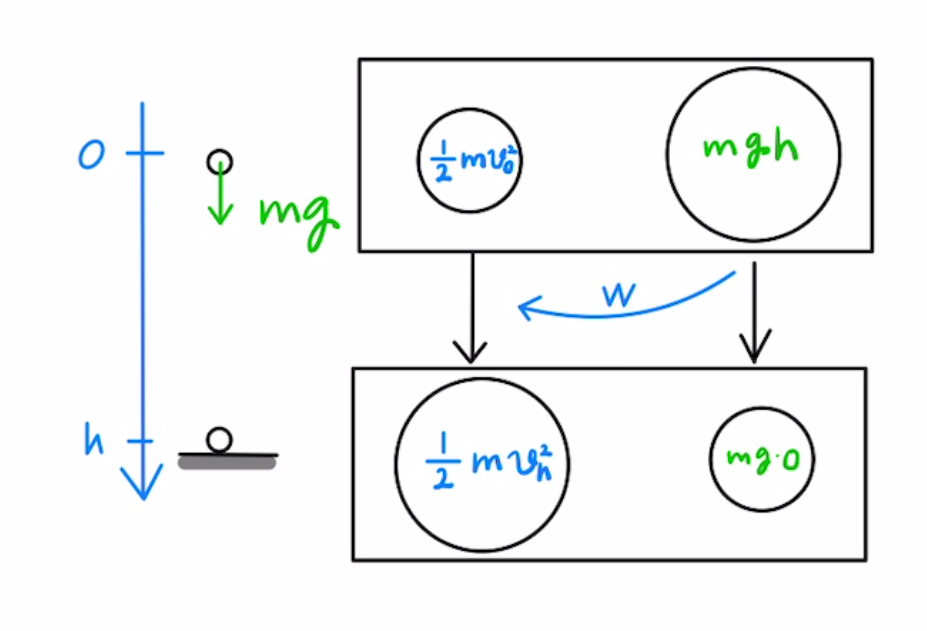
つまり、位置エネルギーは重力$f=mg$が仕事をした分だけ減る。
つまり、位置$ x_0 $でエネルギー0になるとすれば
$$U( x ) = – \int_{x_0}^x{ f }dx $$
と定義することができます。
今回の重力は
$$U( x ) = – \int_{0}^h{ mg }dx = mgh$$}
となるわけです。
弾性エネルギー
バネも同様です。
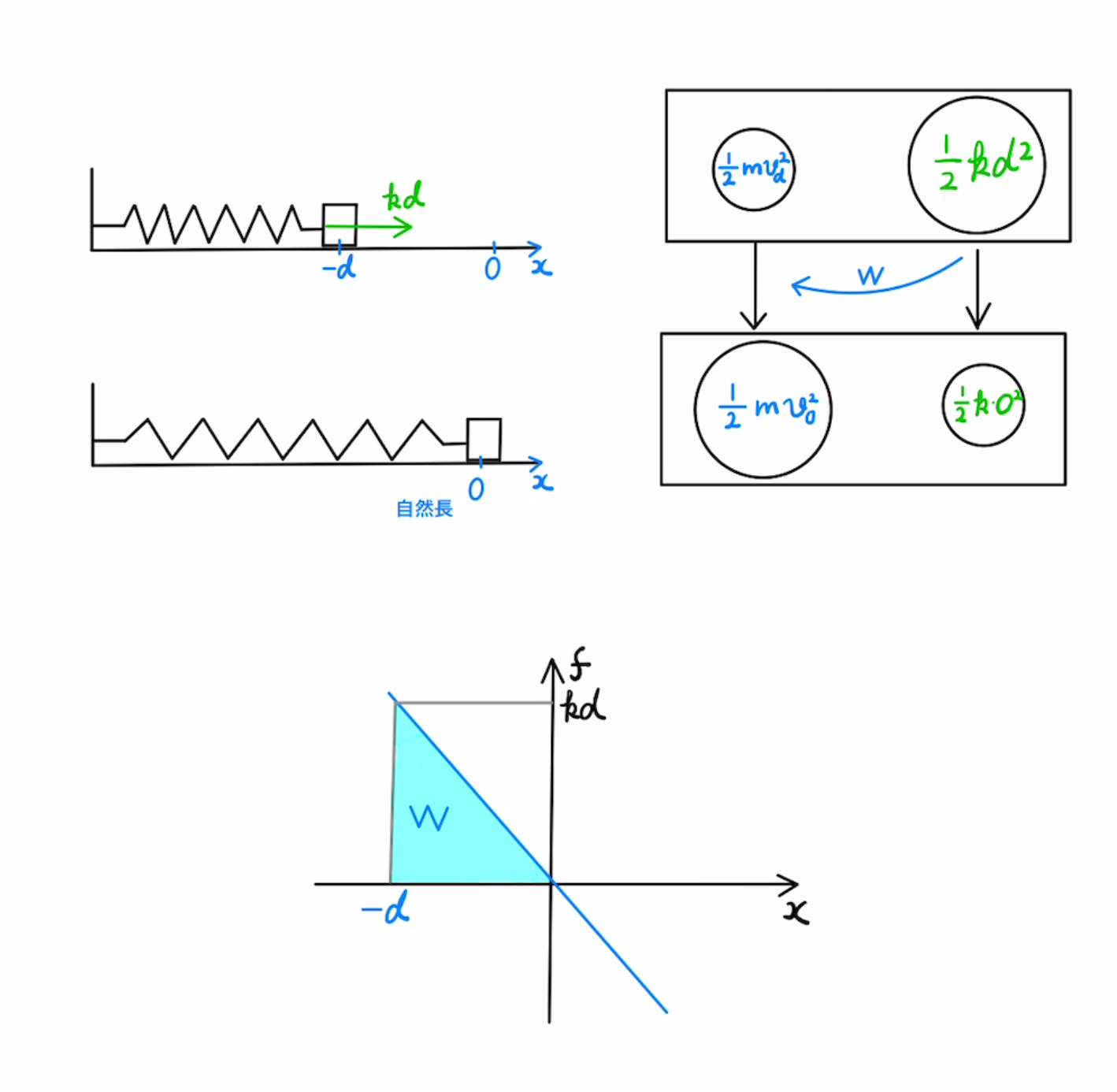
自然長からdだけ縮めた状態から自然長まで伸びる動きを考えると、バネのする仕事$W$は図の面積の部分、$ \frac{1}{2}kd^2$となります。
つまり弾性エネルギーは、 自然長のときを0とすれば $ \frac{1}{2}kd^2$ と置くことができます。
摩擦によるエネルギー損失
次に摩擦に関してはこれは保存力とは言えません。広義な意味でのエネルギー保存にはなりますが、力学的エネルギー保存とは言えません。
まず、静止摩擦ですがこれは摩擦力の方向に動くということはないので仕事をしません。
動摩擦力では一般的にマイナスの仕事をします。言い換えれば物体が床に仕事をする(エネルギーを与える)ことになります。
動摩擦力は$μN$で一定であるため、$l$だけ動いたとき $μNl$だけの仕事をします。 
ではこのエネルギーはどこにいくのでしょうか?
答えは単純で熱エネルギーとなります。
物体と床の粗い表面同士がこすれることで分子の振動に置き換わり、熱エネルギーになり、空気中に放出されます。
このことから、力学的エネルギーとしては保存されません。
平面での仕事
ここまでは1次元の状況、つまり$x$方向しか考えてこなかったのですが、実際には$y$方向(場合によっては$z$方向)も考えなくてはなりません。
この場合はベクトルを使って表記をします。
$$ Δ \left[{ \frac{1}{2}m \vec{v}^2 }\right] = \int _{ \vec { 0}}^{ \vec{ h}}{ \vec {f} d \vec{x} } $$
微小量の内積と聞くと難しそうですが、それぞれの成分で考えていけばいいだけです。
右辺のそれぞれのベクトルは
$$ \vec{f} = \begin{bmatrix} f_x \\f_y \end{bmatrix}, d \vec {x} = \begin{bmatrix} dx \\dy \end{bmatrix}$$
となるため、
$$ \int _{ \vec { 0}}^{ \vec{ h}} { \vec{f} d \vec {x} } = \int _{0}^{h} {f_xdx} + \int _{0}^{l} {f_ydy } $$
と$x$成分と$y$成分のそれぞれに分解することができます。
この式では、$h$だけ下に下がり、$l$だけ横に移動していることを想定しています。
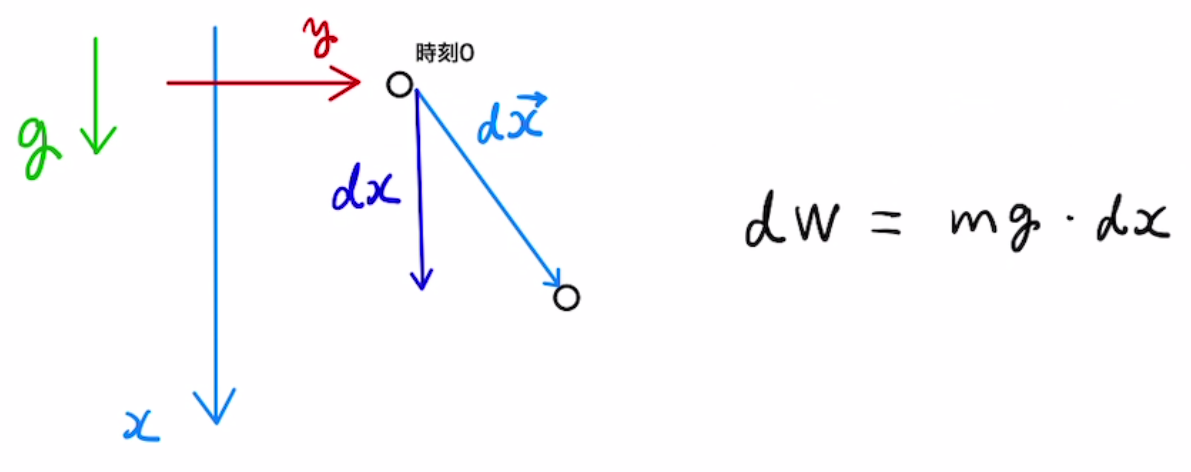
重力の場合は$y$成分の力$f_y$は$0$なので$ \int{mgdx} $だけとなります。
つまり横方向にどう動こうとも、押し下げた分だけ仕事をしたことになります。
結果として、どのような経路を通ろうとも重力がhだけ下に押し下げたなら$mgh$だけ仕事をしたことになります。
また、ここから力の持つエネルギー $U(x)$ も一般化できます。
エネルギーは相対的なものなので、エネルギー$0$となる基準となる位置を$\vec{x_0}$としましょう。
力が仕事をした分だけ $U(x)$が減少することを考える。つまり、$ \vec{x_0} $から $\vec{x}$までした仕事$W= \int_ \vec{x_0}^ \vec{x} { \vec{f}} d \vec{x} $ 分だけエネルギーは減少することから、
$$U( \vec{x} ) = -\int_ \vec{x_0}^ \vec{x} { \vec{f}} d \vec{x} $$
垂直抗力の仕事
垂直抗力は常に動く方向と垂直に力がかかるため、 $ \int{ \vec{N} d \vec {x} } = 0$
つまり垂直抗力がする仕事は$0$となります。
まとめ
外とエネルギーのやり取りがなければ、エネルギーの合計はいつも等しい。
力によりエネルギーを与えるのを仕事をするといい、与えられるのを仕事をされたといいます。
運動エネルギー: $ \frac{1}{2}mv^2$ 速いほどエネルギーが高い
位置エネルギー:$mgh$で高いほどエネルギーが高い
弾性エネルギー: $ \frac{1}{2}kd^2$ 自然長から離れるほどエネルギーが高い
摩擦:$μNl$だけエネルギーを奪う
垂直抗力:仕事をしない
その他の力の仕事:$ \int{ \vec{f} d \vec {x} }$の仕事をする。これは力方向に動かした分だけの仕事と同等である。