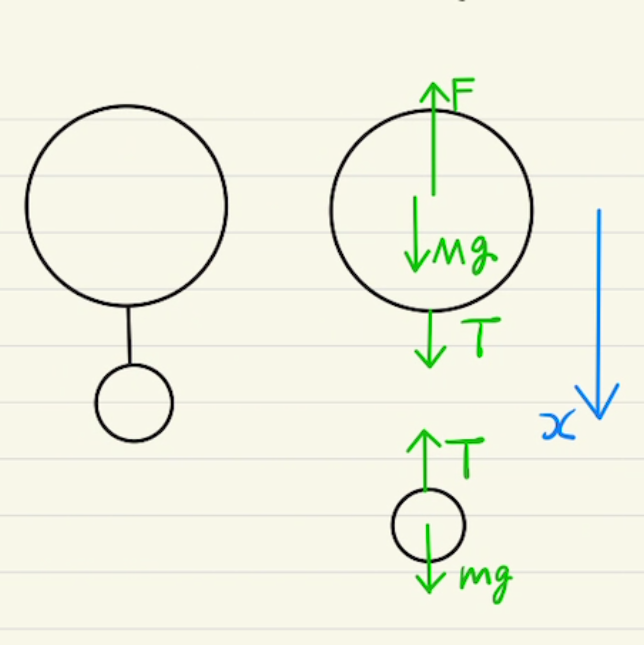
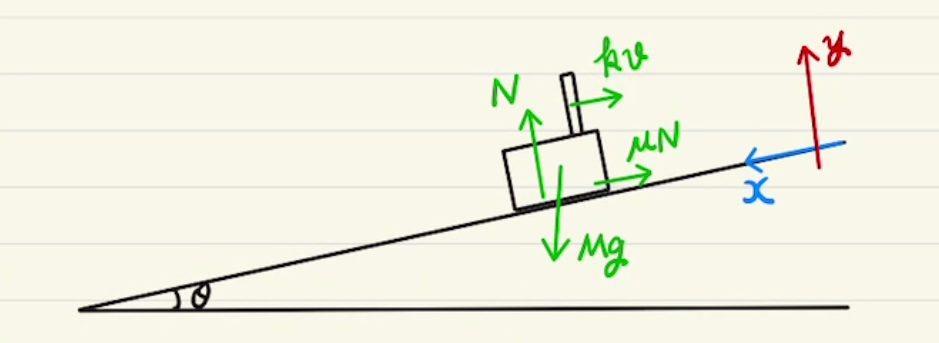
力学のもっとも重要な式、運動方程式の話から始めます。
$$ma=f$$
$m$は質量、 $a$は加速度 、 $f$は力。
これが運動方程式となります。
ではこの運動方程式について分析してみましょう。
運動方程式はベクトルの式
上に出てきた運動方程式は数直線上でしか考えていません。
実際には平面なら2方向、立体空間なら3方向考えなくてはいけません。
運動方程式をベクトルで表記すると下の式になります。
$$m \vec {a} = \vec {f} $$ 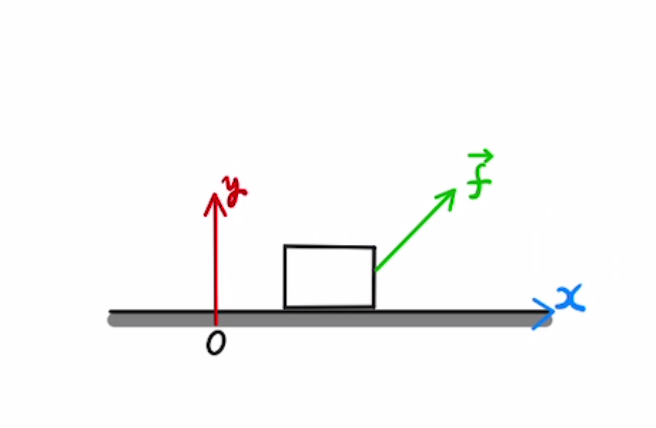
そのため、座標系の設定が最優先となります。
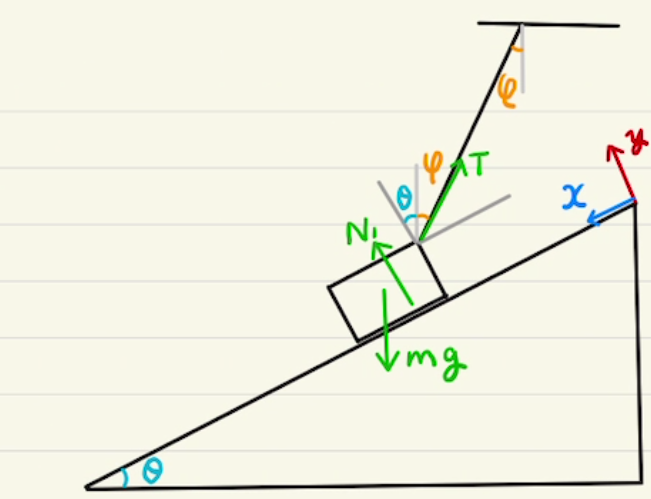
どの方向が$x$か、その方向が$y$かを決めましょう。
どの方向で決めても問題ありませんが、計算が楽になるようにするのがいいでしょう。
通常は水平方向を$x$、垂直方向$y$とおきます。
ベクトルといってもそれぞれの力関係を、要素ごとに見ると考えてください。
$$ ma_x = f_x $$
$$ ma_y = f_y $$
これが運動方程式の要素ごとの式です。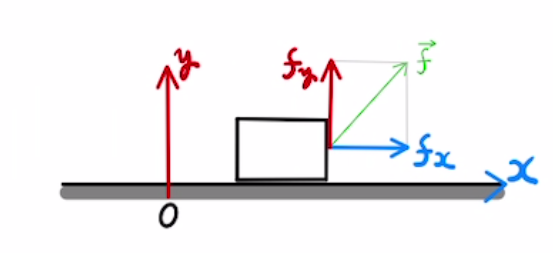
つまり、$x$方向の加速度は力の $x$成分だけで決まるということです。
fは合力
現実の世界では一つの物体に複数の力がかかっています。
$ \vec {f} $はそれらの合力となります。
すなわち、それらの合計が力(ベクトル)となります。
$$ \vec{f} = \vec{f_1}+ \vec{f_2} + \vec{f_3} + … $$
これもただの要素ごとの足し算となります。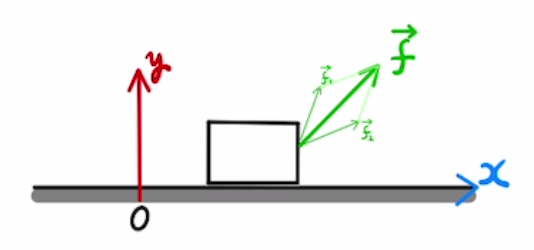
また、加速度 $ \vec{a} = \vec{0} $のとき、合力が$ \vec{0} $となります。
これを力のつり合いといいます。
このとき$x$方向と$y$方向のどちらも力の合計が$0$になります。
加速度が $ \vec{0} $ ということは、静止していなくても速度が一定なら力のつり合いが成り立つので注意してください。
加速度と速度、位置の関係
運動方程式の両辺を$m$を両辺で割ると
$$ \vec{a} = \frac{ \vec{f}}{m} $$
右辺が原因、左辺が結果という形になります。
言葉にすると、力が大きければ大きいほど大きく加速し、質量が大きければ大きいほど加速しにくいということを表します。
さて、加速度とはなんなのかを見ていきます。
加速度の定義は速度を時間微分したものです。逆に加速度を積分すると
速度は位置の時間微分です。
初速度を$v_0$、初期位置を$x_0$とすると下の図のような関係がわかります。
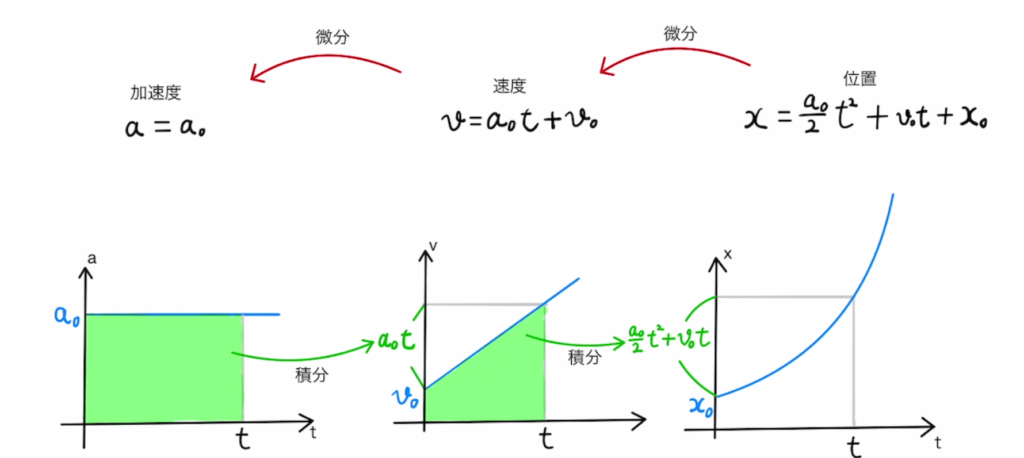
このことから、運動方程式から加速度がわかる→積分により速度や位置がわかるというのが運動方程式の基本的な使い方になります。
初速度$v_0$、初期位置$x_0$は積分定数となっていることがわかりますね。
このグラフを毎回三つとも描くのは面倒なので、基本的には真ん中のv-tグラフだけ書きます。
v-tグラフの傾きは加速度、面積が変位(位置の変化分)となるため、すべての情報が一目でわかりやすくなります。
よく出てくる力
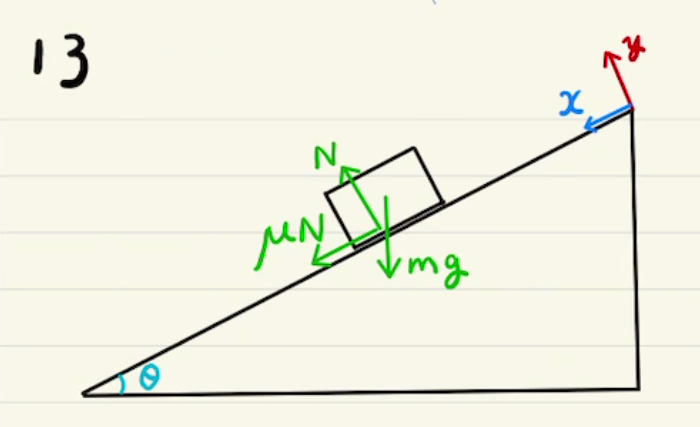
・重力 mg
いまさらだと思う方もいると思いますが、質量と重さは少し異なります。
重さは地球上では質量に比例しますが、宇宙空間に行くとほぼ$0$になります。
逆に重力の強い木星では重くなります。
一方で質量は物体が固有に持つもので宇宙空間でも他の惑星でも変わりません。
つまり、
$重さ(=重力)f=質量m×重力の強さg(重力加速度)$
となります。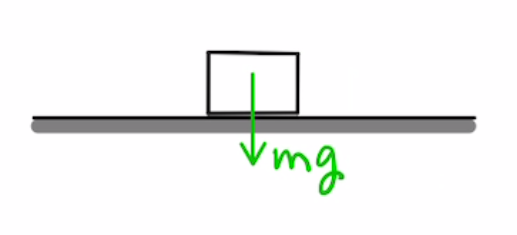
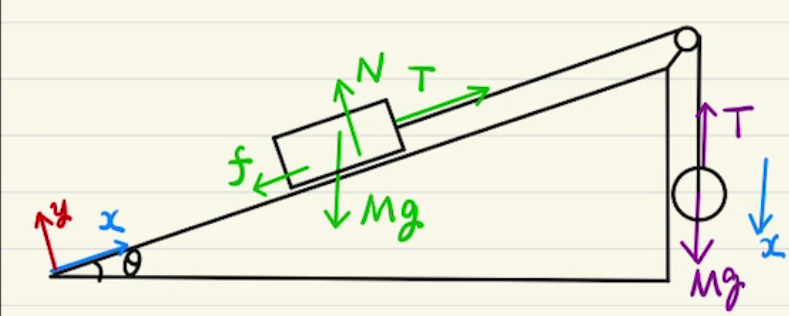
・垂直抗力 N
地面に接している際に地面垂直方向に動かないように力がかかります。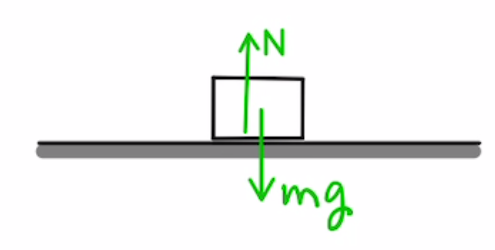
・摩擦力 $F_r$
動摩擦力と静止摩擦力があります。
静止摩擦力は物体が静止しているときに物体が動かないようにかかる力です。
静止摩擦係数を$μ_0$とすると静止し続ける条件は
$F_r<μ_0N$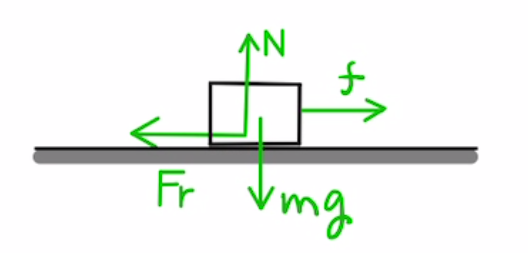
動摩擦力は物体が動いているときに動いている方向とは逆向きにかかる力です。
静止摩擦係数を$μ$とするとかかる動摩擦力 は
$F_r=μN$ 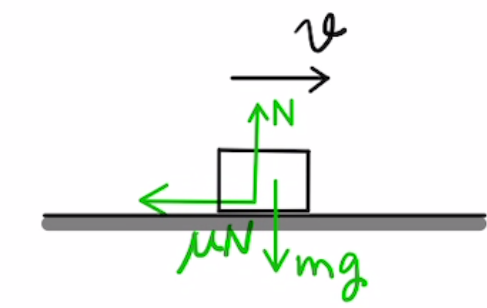
まとめ
運動方程式は以下の方法で解いていくことが基本となります。
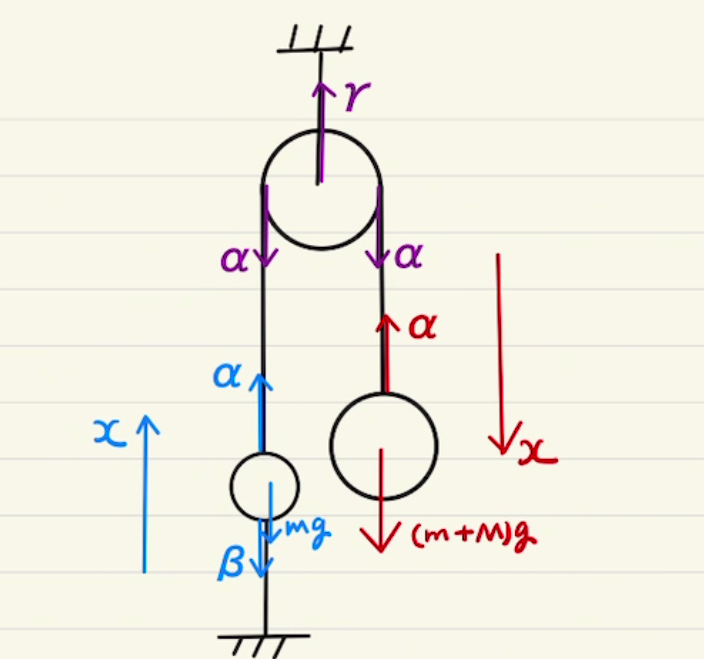
・図を描き、力の大きさと方向を書き込む。それに合わせて$x,y$の座標系も設定する。
・運動方程式から加速度を求める。この方程式はベクトルであることに注意する。
・加速度を積分することで速度や位置がわかる。初速度や初期位置が積分定数となる。
・数式でわかりにくければv-tグラフを描くといい。傾きが加速度、面積が変位となる。