解答欄

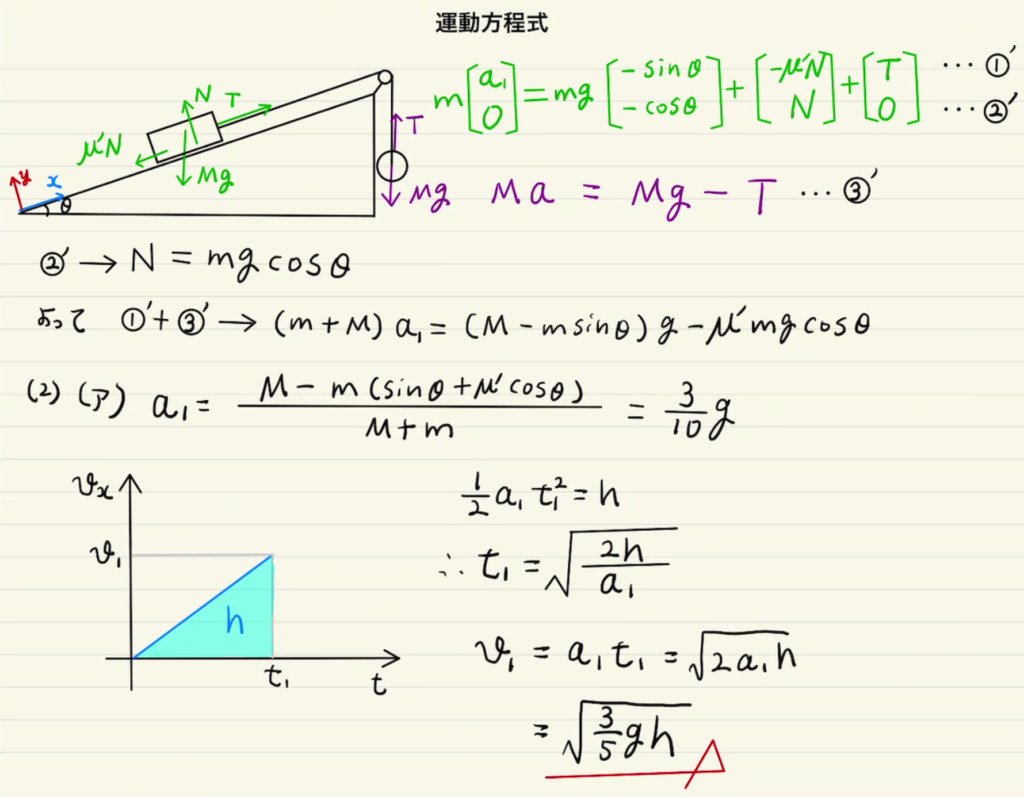
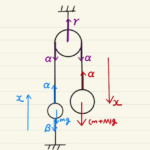
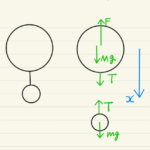
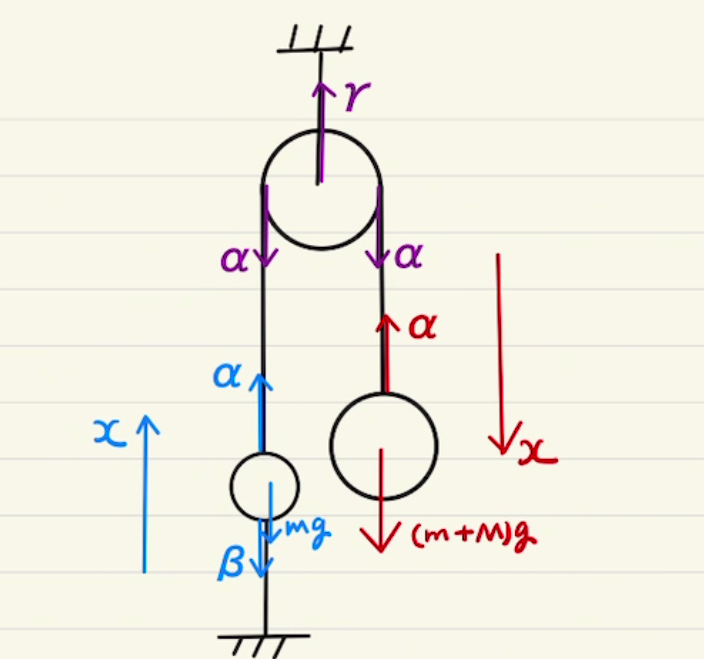
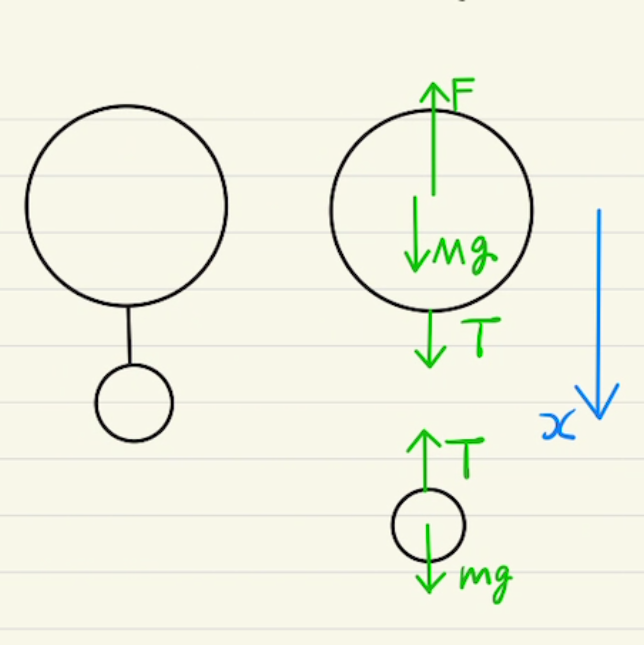
紐でつながれた二体問題ですね。
斜面上の物体は斜面に合わせた座標で運動方程式を立てましたが、吊り下げられている物体は上下だけの運動方程式を立てれば十分そうです。
(1)では静止条件を、(2)では動いたときの動きを見ています。(ア)では重しにより上方向に加速をし、(イ)では重しがなくなるので減速していくという流れです。
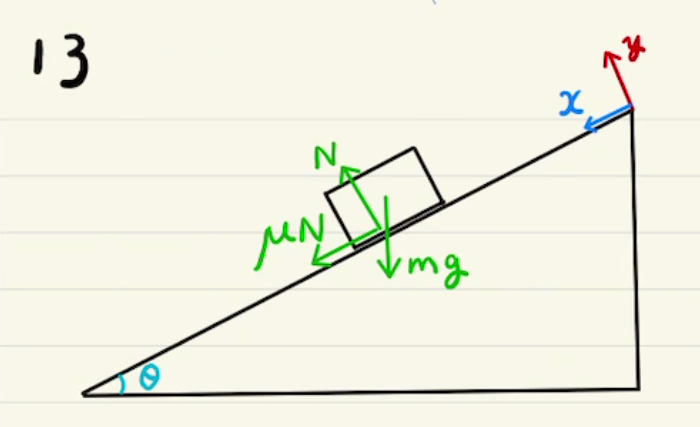
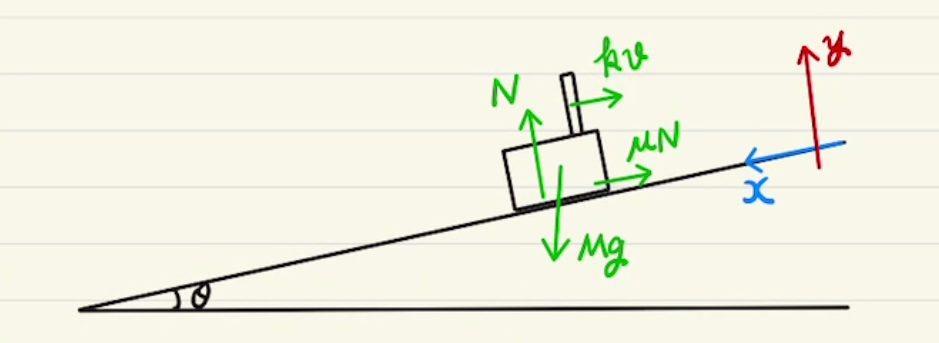
今回も斜面角は$θ$としてます。
(1)からやっかいなのが、上にのぼることも下に滑り落ちることも考えられることです。
そのため、摩擦力$f$は$x$正方向と$x$負の方向両方を考えていかなければなりません。
上の解答では一旦$f$は$x$負の方向であるように定義をし、$f$が負になるときは$x$正方向になるとしました。
この時絶対値から静止条件を定義できます。
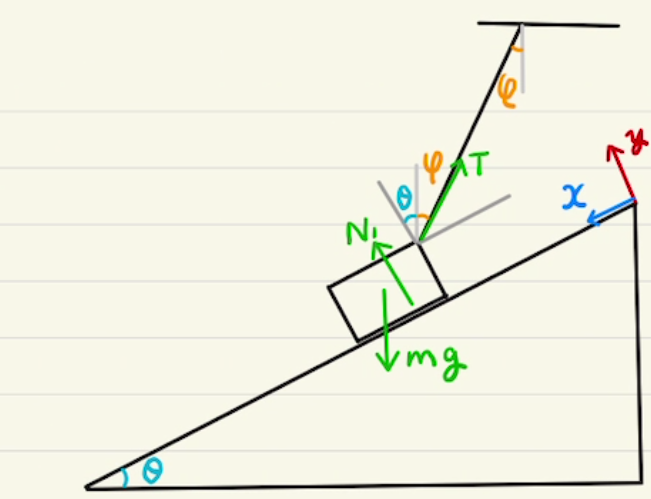
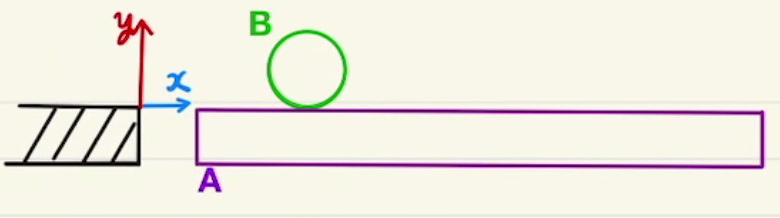
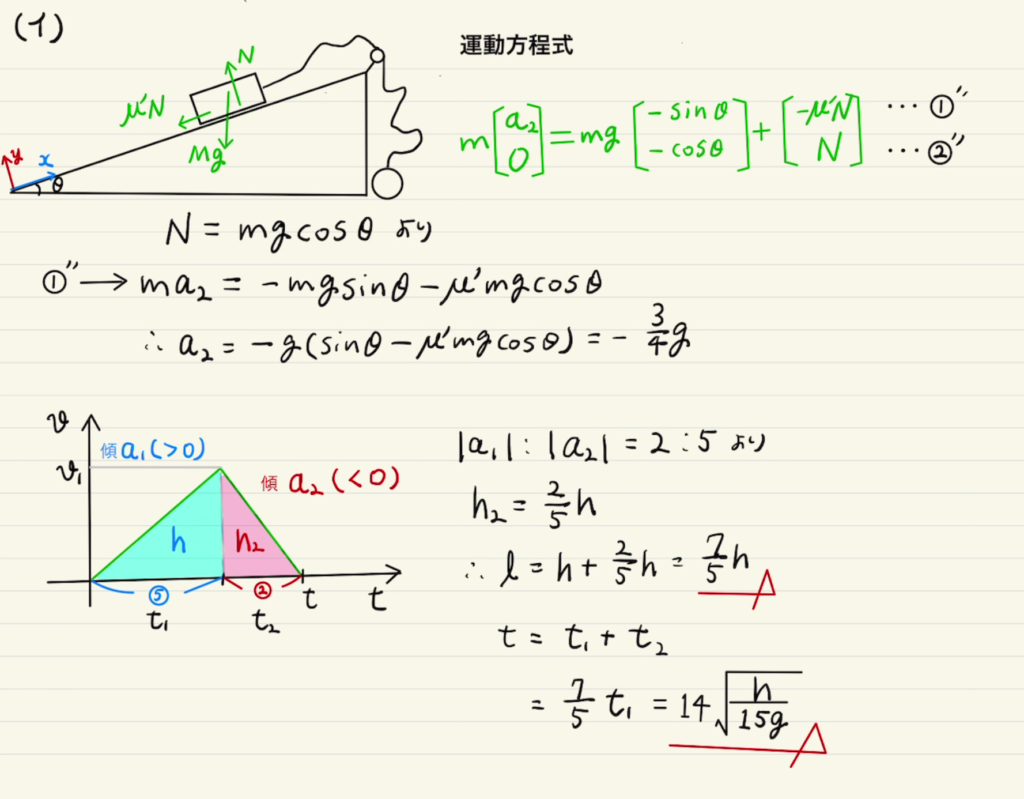
(2)(ア)はシンプルで摩擦のある等加速度運動となります。問題は(イ)で、素直に時間1/2 $a_2t^2$を求めて計算してもよかったのですが、答えに$h$を使うので$v$-$t$グラフから比率を見るほうが楽です。
時間の比と移動距離の比は、それぞれ加速度(の絶対値)の逆比になります。