解答欄
解説
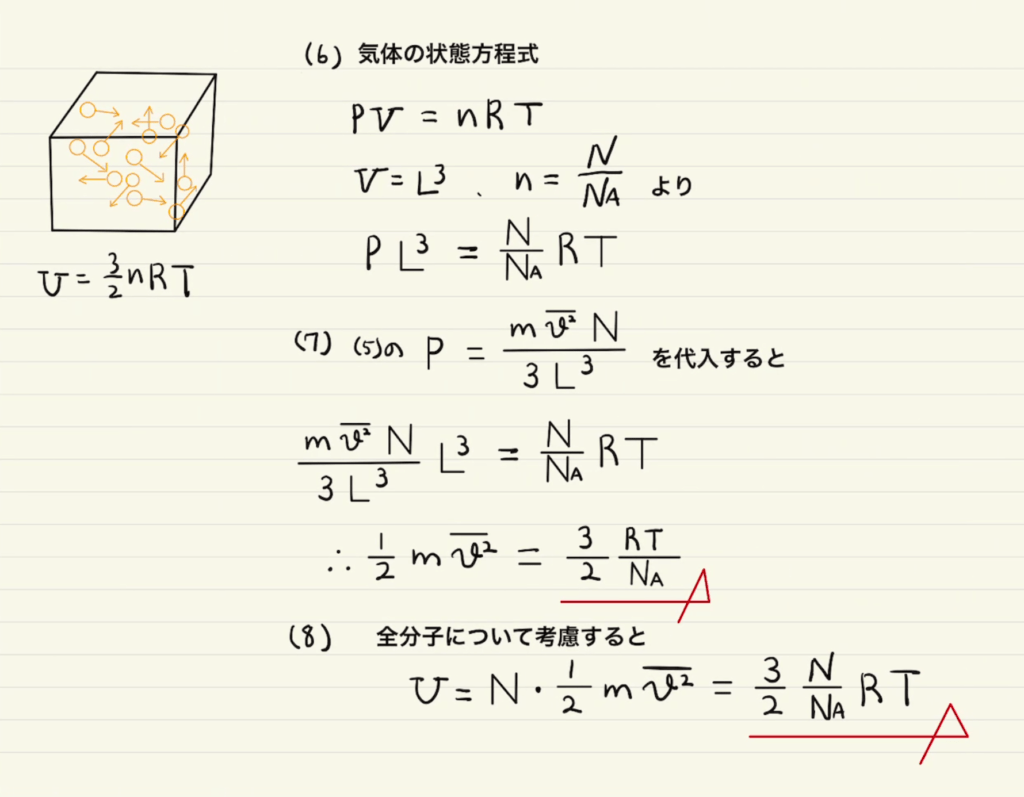
気体のエネルギー=分子の運動エネルギーという事実から、単原子分子の持つエネルギーを計算するものです。
答えは熱力学を一度学んだ人なら見たことある$\frac{3}{2}nRT$となります。
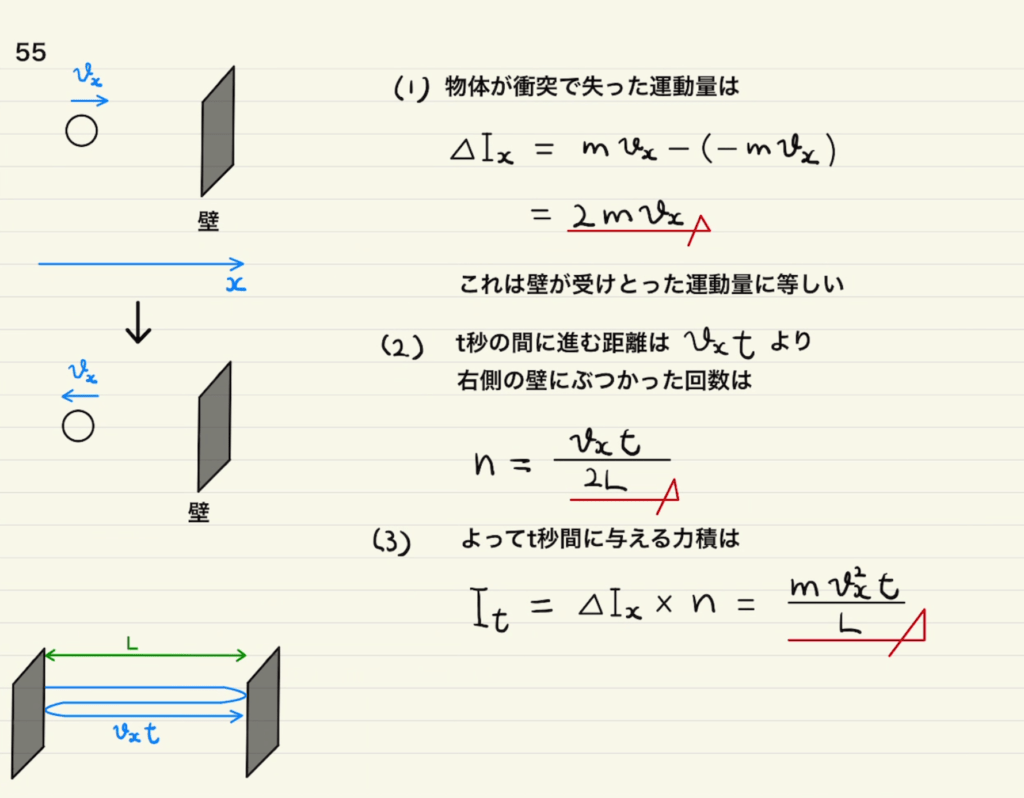
まず分子の運動が壁に与える力積を計算し、それを1秒にぶつかる回数と個数をかけることで期気体が壁に与える力積を求めます。
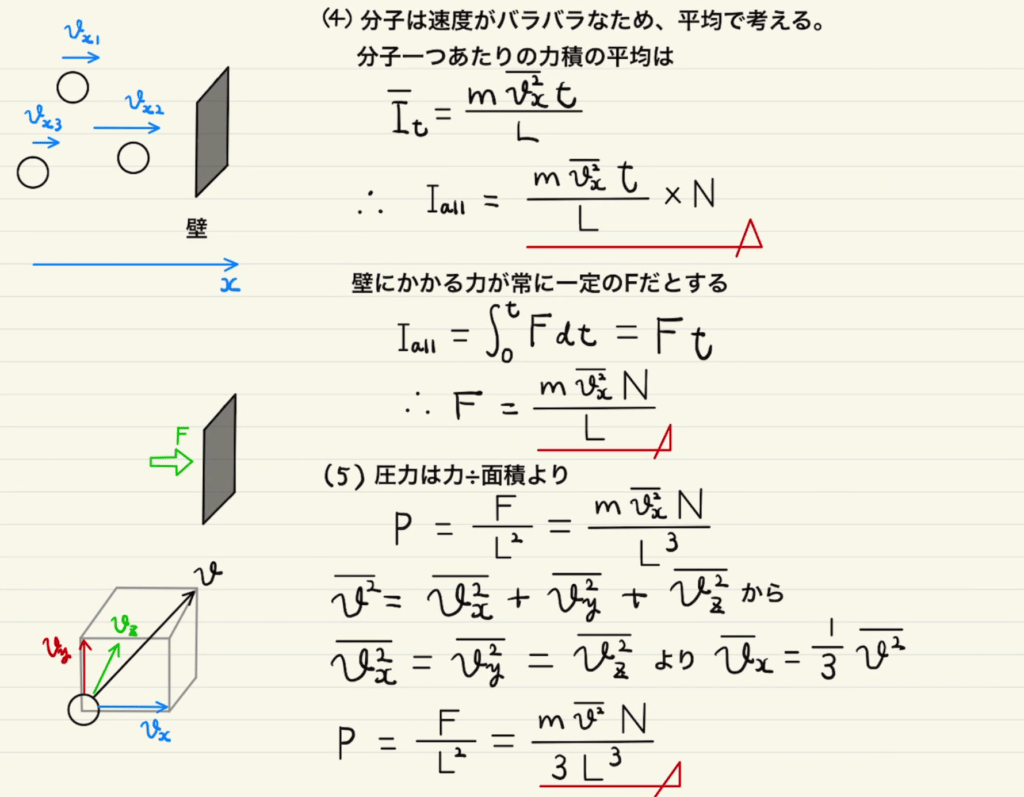
ただし、ここで分子の速度は全て同じではないので、平均を取ります。
なぜ速度ではなく速度の二乗を使うのかと聞かれることがあるのですが、 最終的に求めたいのが分子の運動エネルギー だからです。 $v_x^2$ の平均 とはなにを示すかと言えばエネルギーベースでの平均ということになります。
分子の運動エネルギーの平均は $\frac{1}{2}m\bar{v^2}$ なので $\bar{v^2} $を知ることで気体のエネルギーが計算できます。
これを$I_t$の平均から求めることができます。 (3)で求めた$I_t$に使われている文字のうち、分子ごとに違うのは $v_x^2$ の部分だけになるからです。
$v_x^2$ の平均は速さ(もしくは速度)の平均の二乗とは異なります。
試しに1,2,3,4の四つの数字の二乗の平均をとると7.5ですが、平均の二乗をとると6.25になります。
気体が$x,y,z$方向に均質だとすれば、 $\bar{v_x^2}$ と $\bar{v_y^2}$ と $\bar{v_z^2}$は等しくなり、$\bar{v^2}$を使って書き換えられます。
気体のエネルギーは $\frac{3}{2} \frac{N}{N_A} RT$となりますが、$全分子数N÷アボガドロ数(1mol当たりの分子数)N_A$ は何molかを表すため、 $\frac{3}{2}nRT$ と等しいことがわかりました。
補足ですが、この式が成り立つのは単原子分子の理想気体だけです。
一般に分子の運動の自由度を$L$としたときに気体のエネルギーは$\frac{L}{2}nRT$と言われています。
例えば二原子分子の場合は二方向の回転も考慮にいれるので $\frac{5}{2}nRT$となります。
一般的な分子を考える場合、分子構造や原子間の結合力、温度等によっても変わるため大学入試で扱われることはほとんどありません。
そのため、単原子分子以外の 気体のエネルギーを表す場合は、等積モル比熱$C_v$を使って$nC_vT$と表すのが一般的です。