解答欄
解説
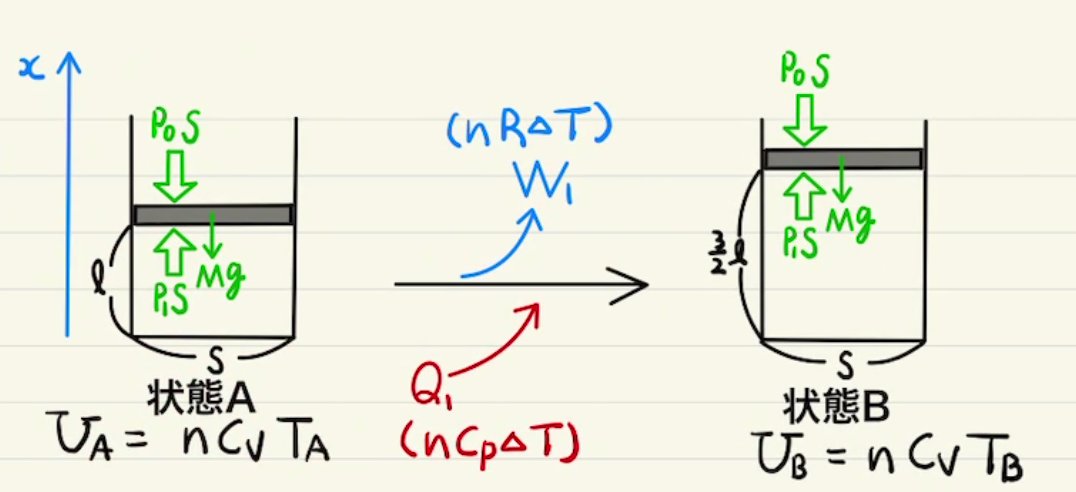
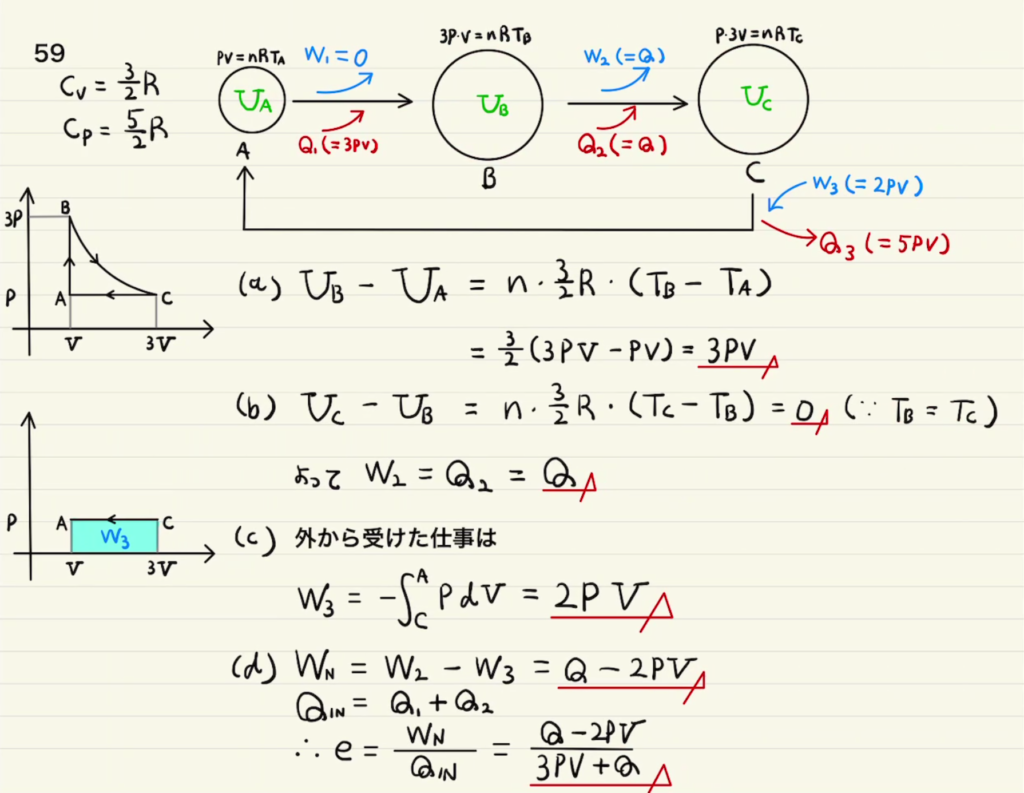
等積変化→等温変化→等圧変化のサイクルを扱ったものとなっています。
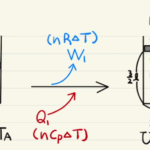
等積では外に仕事をせず $Q_1=ΔU_1$となっています。
等温変化では温度が変化しない=内部エネルギーが変わらないので $W_2=Q_2$となります。
ここで気体が外にする仕事 $W_2 $はP-Vグラフから求められますが、 $Q_2=Q$ となっているので、そのまま $Q$でよいのでしょう。
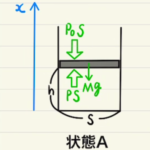
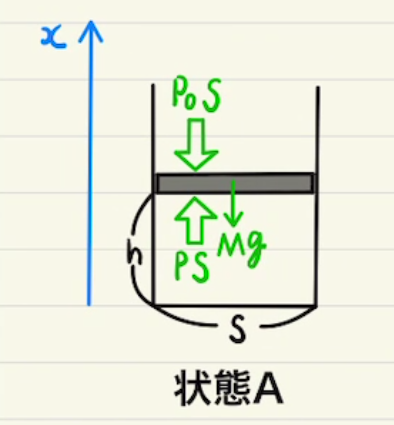
等圧変化では外から受ける仕事 $W_3 = nRΔT = PΔV= 2PV$となり、 C→Aでの内部エネルギー減少は$U_C -U_A = \frac{3}{2}nR(T_C-T_A)= \frac{3}{2}P(V_C-V_A) = 3PV$ なので $Q= W + (U_C – U_A ) =5PV$
単原子分子の等圧変化での $ΔU:W:Q =C_v:R:C_p =3:2:5$は頭に入れておくといいでしょう。
熱効率のサイクルですが”$気体が外にした正味の仕事W_N÷外部から加えた熱量Q_{in}$”となります。
正味の仕事は $気体が外にした仕事ー 気体が外からされた仕事$”です。
エンジンが車輪を回すことを考えてみましょう。エンジンは$W_2$の仕事によって車輪を回すことができますが、 $W_3$分の仕事はまたエンジン側に戻されます。
そのため正味の仕事(実質的に気体がした仕事)は$W_N = W_2ー W_3$ となります。
一方で エンジンに仕事をさせるために熱を与えています。それは入ってきた熱の合計$Q_{in} =Q_1+Q_2$です。外に出した熱 $Q_3 $はただの廃熱となるため考慮されません。サイクル上は全くの無駄になっていると考えます。
このことから効率$e=\frac{外にした仕事-外からされた仕事}{外からの加熱}$となります。
補足
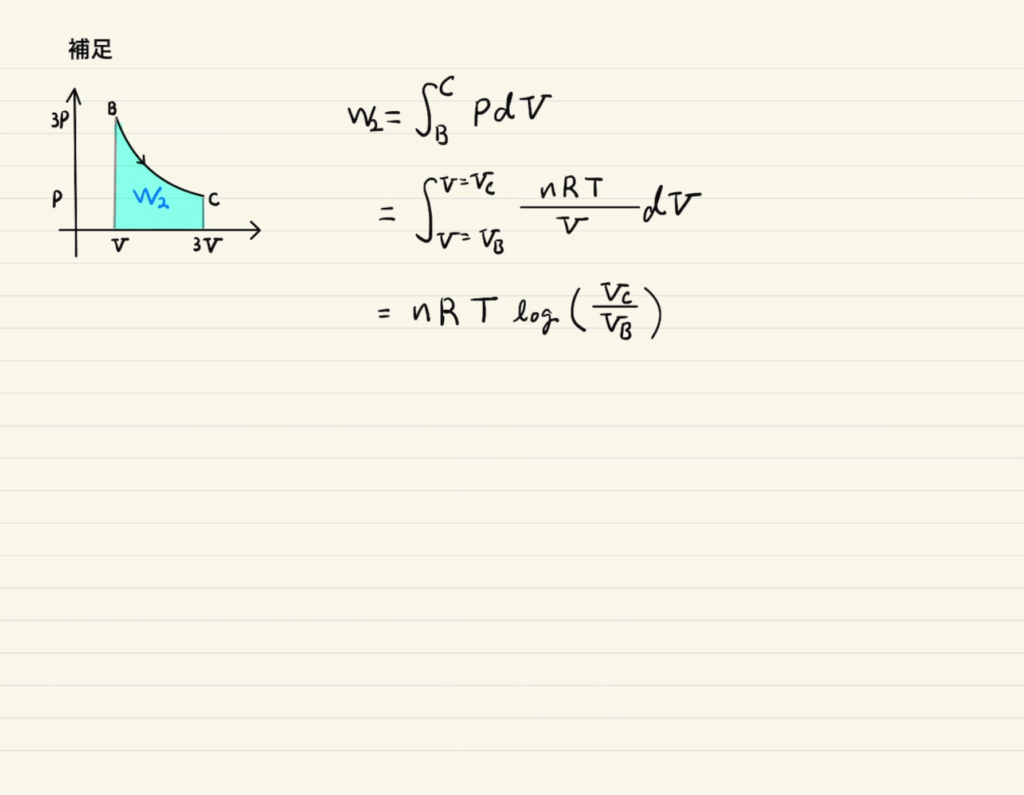
(b)の仕事を$W_2$は図の面積の部分なので積分をすればQを用いなくても答えがでます。
本来ならこれも答えとなるはずですが、積分での解答は高校範囲に含まれていないので、こちらの想定はしていないのでしょう。