慣性力とは、見ている視点によってあたかも力がかかっているように見える現象を指します。
電車で加速しているときは後ろに引っ張られているように感じ、急ブレーキがかかると前に押し出されたように感じるあれです。
実際にそれを数式で、見ていきます。
まず、動いている電車の内部の座標系X-Yと外部の座標系x-yの二つの座標系を考えます。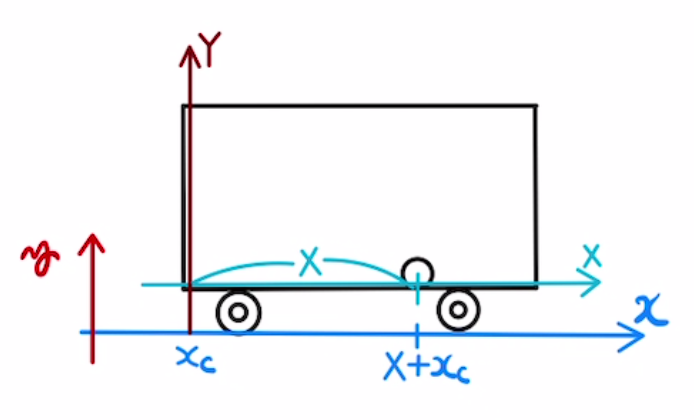
図のように$X$軸と$x$軸が$x_c$だけズレているとしましょう。
このとき座標の関係は
$$x=X+x_c$$
となります。
両辺を時間で微分すると
$$v=V+v_c$$
これも感覚的にわかる話だと思います。
電車内で速度Vで歩いている人が、外部から見たら電車の速度分プラスされて動いているように見えます。
さらに時間で微分すると
$$a=A+a_c$$
となります。
加速度$a_c$で電車内で動く物体は、電車の中では加速度$A$で動いているように見える場合、外部からは加速度 $A+a_c$で動いているように見えることを示しています。
これを運動方程式$ma=f$に代入してみます。
$$m(A+a_c) = f $$
これが外から見た物体の運動方程式となります。
両辺から$ ma_c $引くと
$$ mA = f – ma_c $$
これが内側から見た物体の運動方程式になります。
内部から見ると、加速度と反対方向に $ma_c$だけ力がかかっているように見えるわけです。
これは一般的に二次元や三次元でも成り立ち、
$$ m \vec{ A }= \vec{ f }- m \vec{ a_c }$$
となります。
まとめ
外部から見て加速度$\vec{a_c}$で動いている座標系では、内部から見ると物体は$-m\vec{a_c}$の力を受けているように見える。