解答欄
解説
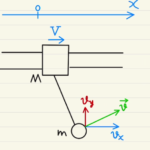
慣性力について見る良問かつ難問。
基本的に慣性の問題といっても外から見れば通常の運動の問題だし、内部の視点(今回はA視点)から見れば慣性力があるように見えるというだけのはなしです。
そのため、二通りのやり方で解けます。
一つ目は外部視点での運動方程式です。
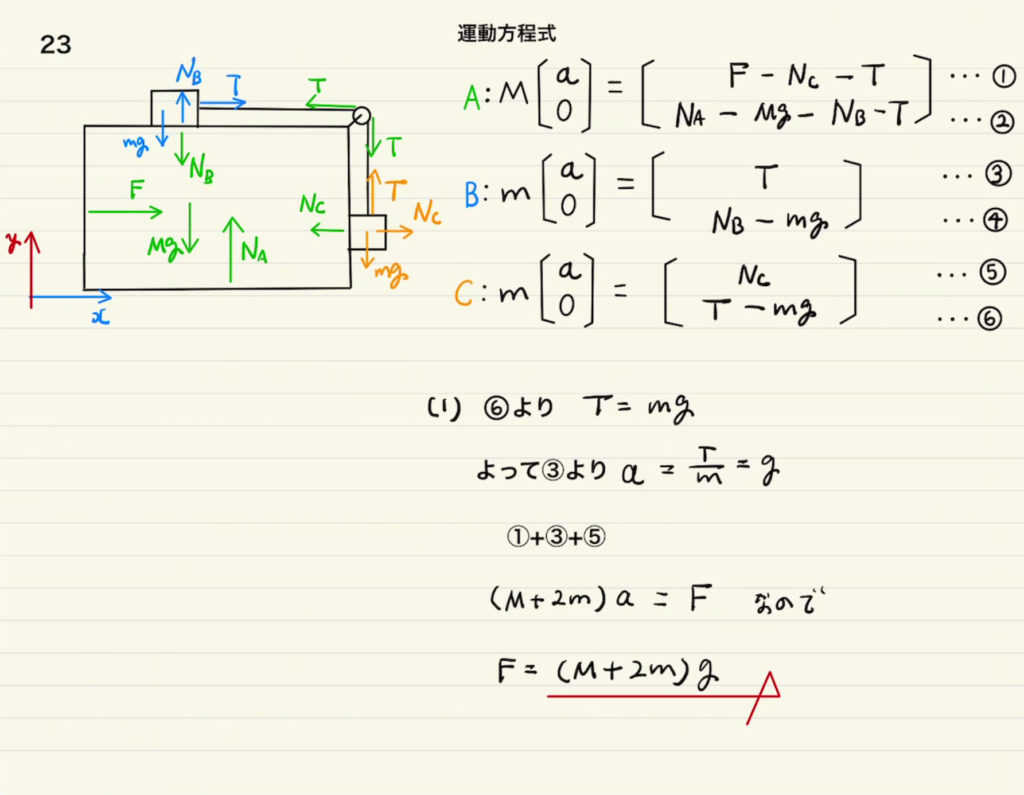
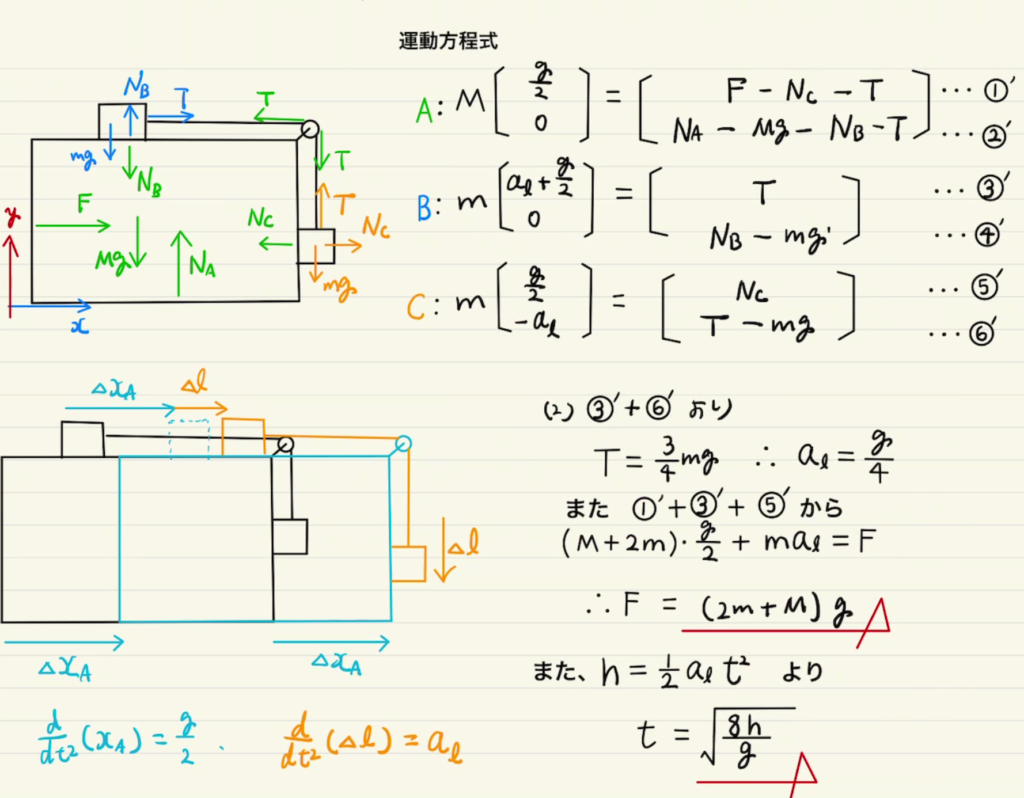
一応$A,B,C$についての$x,y$それぞれの運動方程式を立てました。今回の問題では②の式はなくても大丈夫だが、方程式をしっかり立てれば解けない問題はなくなるはずです。
(1)については単純で$A,B,C$全ての加速度は$x$方向に$a$で一定でありわかりやすいです。
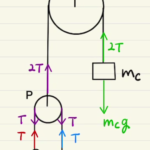
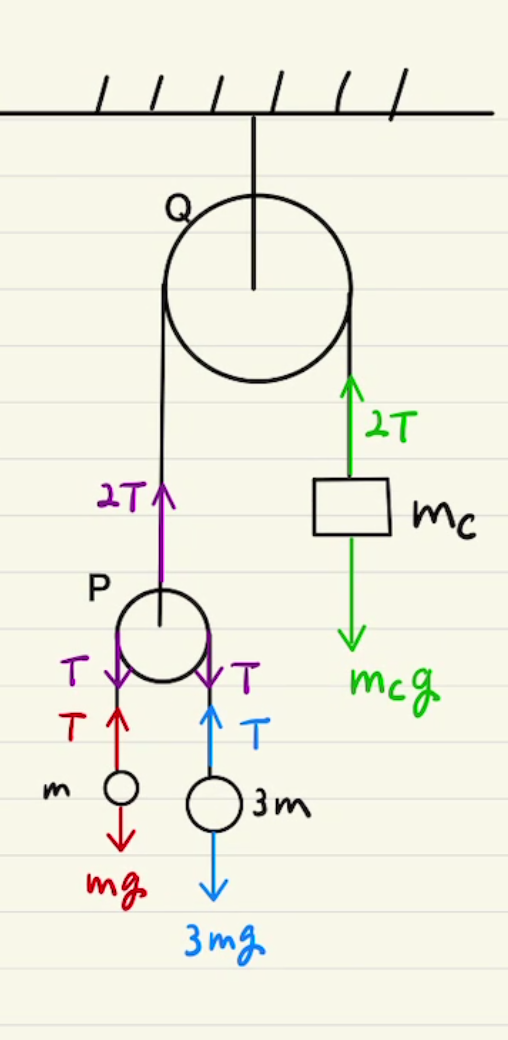
滑車はAに固定されているため、滑車にかかっている力もお忘れなきよう。
(2)は拘束条件が非常にわかりにくくなっているが、紐の変位$Δl$とし、速度( $Δl$ の時間微分)を$v_l$、加速度を$a_l$ ($v_l$ の時間微分) と置きます。 それを軸に運動方程式を立てます 。
Bのx方向の変位は$Δx_A+Δl$から時間微分を二回して $a_A+a_l$となることがわかれば、 $a_A = \frac{g}{2}$ なので加速度の変数は $a_l$だけでよくなります。
未知の変数は$F,T,N_A,N_B,N_C$そして$a_l$の六つなので6個の式から求められます。
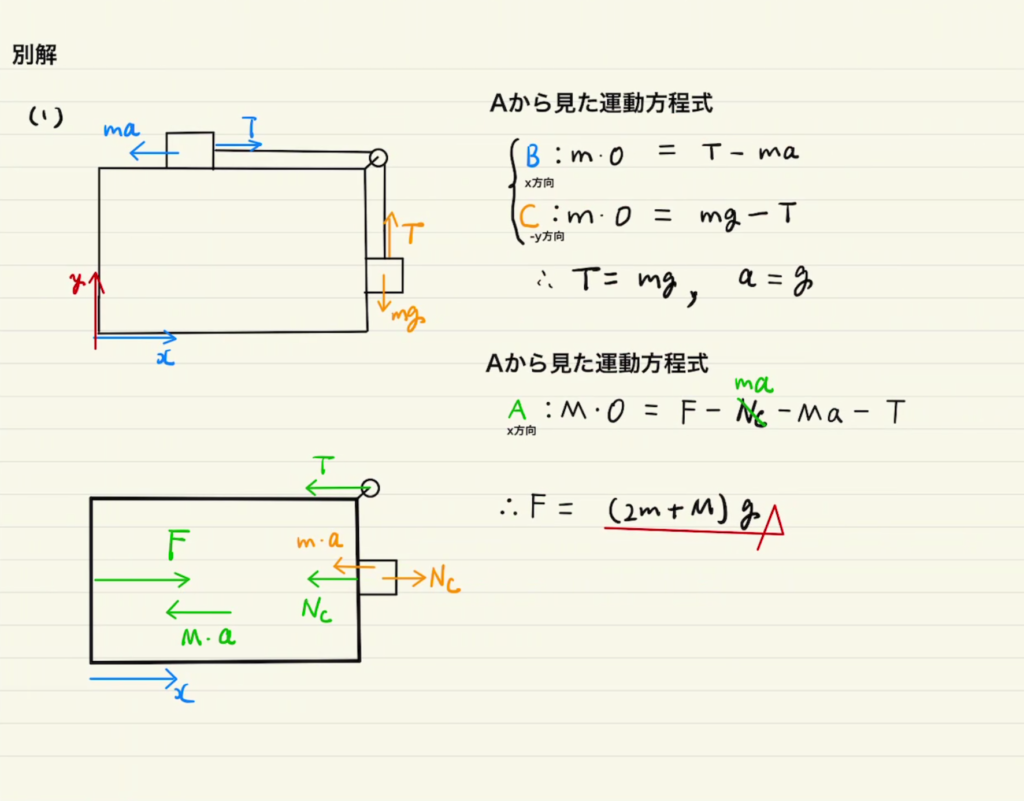
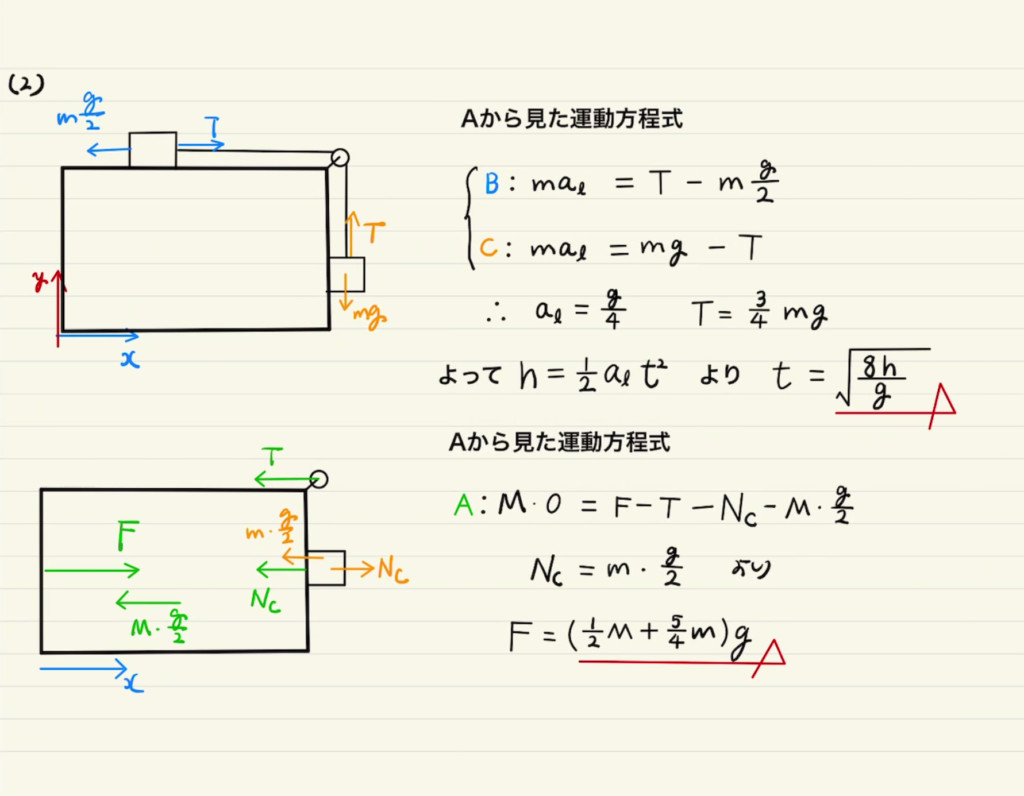
二つ目の解き方は外部視点での運動方程式です。
一つ目の解き方に比べて煩雑でなく、拘束条件も深く考える必要がないので非常に楽です。
ただし、Cの$y$方向の運動方程式を立てなくてよいといっても垂直抗力は発生します。