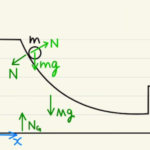
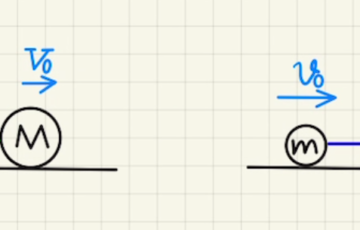
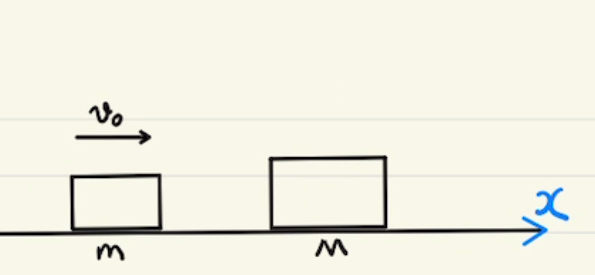
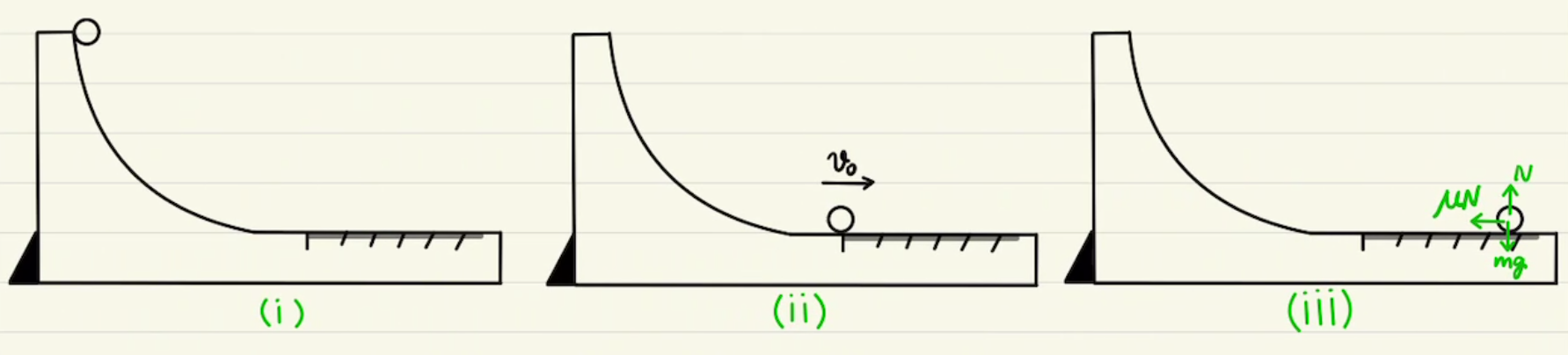
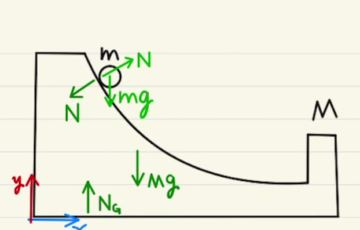
今回の作図では箱は上下方向に動かないため、箱を質点として扱い、平行にスライドする状況と同じと考えます。
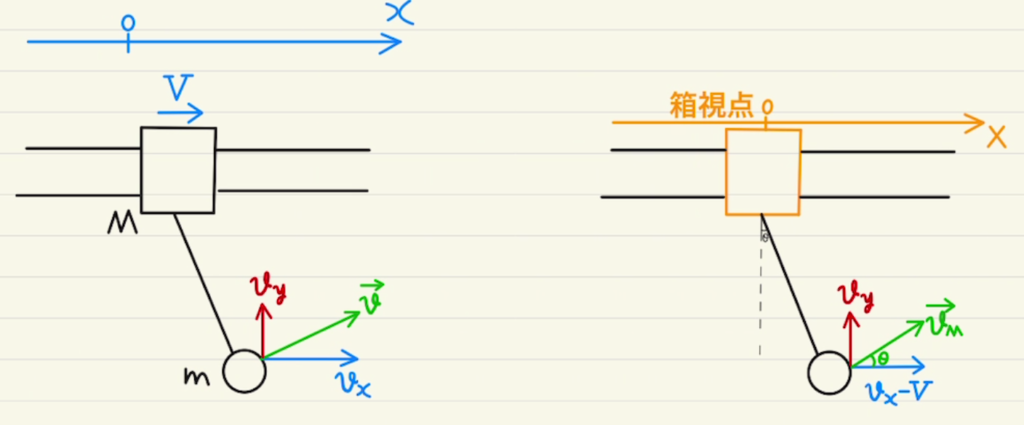
今回の問題ではPと箱同士の作用反作用を除くと、$x$方向に力が働いていません。
よって$x$方向の運動量保存が成り立ちます。
また、 $y$方向にはPと箱同士の作用反作用を除き、重力と垂直抗力だけが働いています。そのため、垂直抗力は仕事をせず重力以外で外とエネルギーのやりとりをすることはありません。
そのため $y$方向の運動量保存は成り立ちませんが、位置エネルギーを含めることでエネルギー保存則が成り立ちます。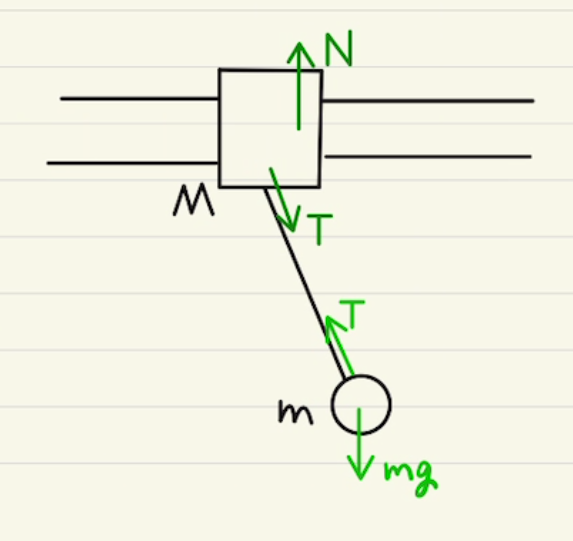
このことから $x$方向の運動量保存とエネルギー保存則を使って解いていくことが基本となります。
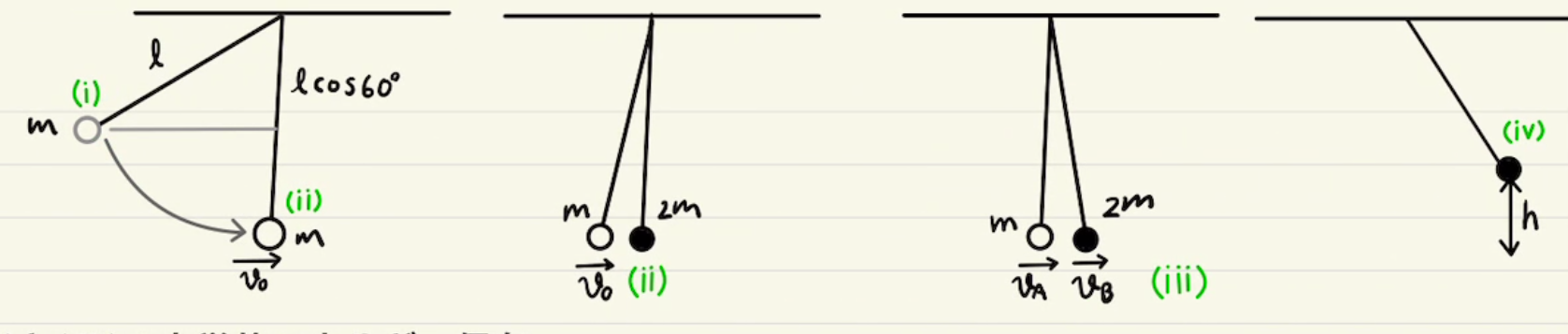
(1)(2)では上のような変化となります。
ここから 運動量保存 と 力学的エネルギー保存則の連立で未知数である$ v_1 $と $ \cos{θ_0} $を求めます。
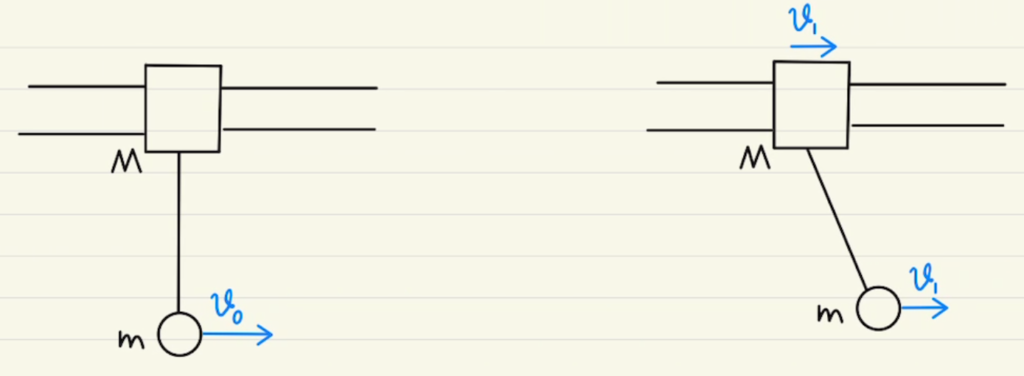
(1) $x$方向の運動量保存 より
$$mv_0=(m+M)v_1$$
よって
$$v_1=\frac{m}{ m+M }v_0$$
(2)力学的エネルギー保存則より
$$\frac{1}{2}mv_0= \frac{1}{2}(m+M)v_1+mgl(1-\cos{θ_0})$$
これに(1)の答えを代入すると
$$ \cos{θ_0} = 1- \frac{Mv_0}{2(m+M)gl} $$
(3)(4)も初期条件がことなるだけでやることは同じで、 運動量保存 と 力学的エネルギー保存則の連立をし、未知数 $ v_3 $と $ V_3 $ を求めます。
ただし(4)は位置を求められているため、運動量保存を時間積分した式を使います。
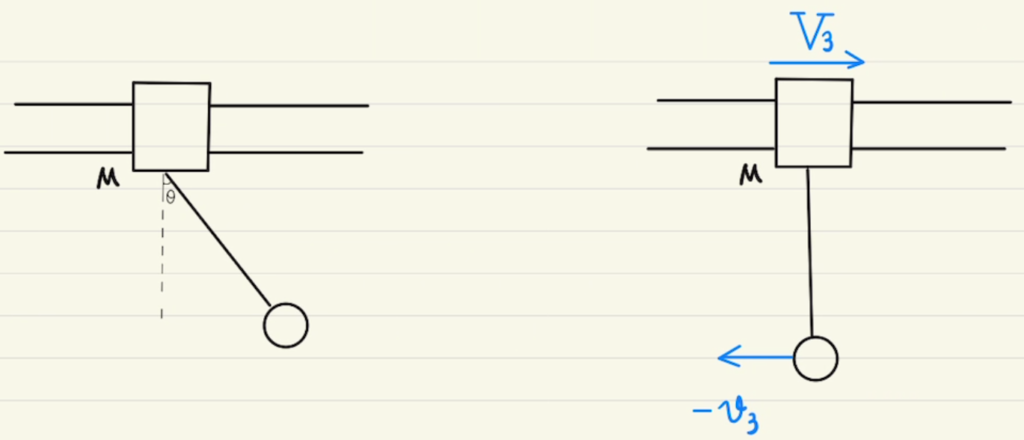
(3)
$x$方向の運動量保存 より
$$0=mv_3+MV_3$$
力学的エネルギー保存則より
$$ mgl(1-\cos{θ}) = \frac{1}{2}MV_3+ \frac{1}{2}mv_3 $$
よって二式より
$$ V_3 = m\sqrt{\frac{2gl(1-\cos{θ}) }{M(m+M)}} $$
$$ -v_3 = \sqrt{ \frac{2gl(1-\cos{θ}) }{m+M}} $$
(4)

初期状態から最下点前の状態までの運動量保存則は
$x$方向の運動量保存 より
$$0=mv_x(t)+MV(t)$$
これを時間で積分すると、
$$C_1=mx(t)+MX(t)$$
となり、これが常に成り立つことがわかります。
$x(0)=0,X(0)=l\sin{θ}$より、
$$ mx(t)+MX(t)= l\sin{θ} $$
最下点に達するときは $x(t)=X(t)$ となるため、
$$X(t) = \frac{m}{m+M}l\sin{θ}$$
補足
運動量保存則を時間積分した式
$ mx(t)+MX(t)= l\sin{θ} $
は、変形すると、
$ \frac{mx(t)+MX(t)}{m+M}= \frac{ l\sin{θ}}{ m+M } $
この左辺は二物体の$x$方向の重心 $x_G (t)$の定義となります。
つまり重心位置$ x_G(t) =一定$。
これが成り立つ条件は、外力が$0$かつ重心の初速度が$0$の時となります。
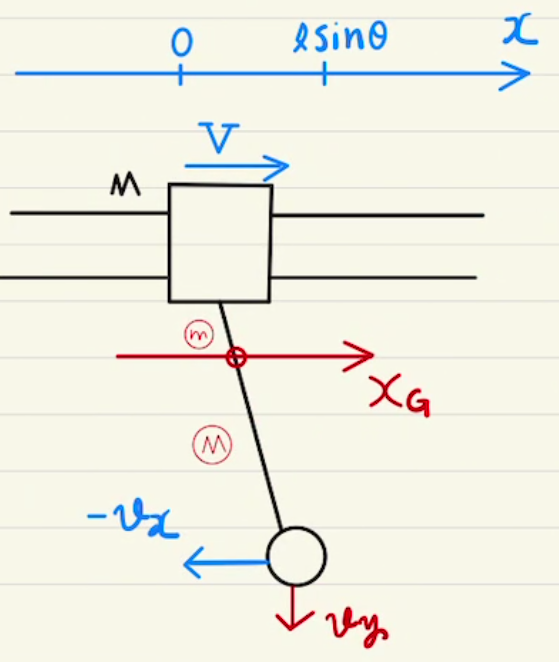
また、運動量保存則を時間積分した式は初速が $0$ でなくても成り立ちます。
両物体の$x$方向の初速度をそれぞれ、$V(0),v_x(0)$とすると
$ mv_x(t)+MV(t)= mv_x(0)+MV(0) $
より、
$ mx(t)+MX(t)= C_1 + ( mv_x(0)+MV(0) )t $
となります。$ C_1 $は$t=0$を代入して求まり、$ C_1 = mx_x(0)+MX(0)$となります。
よって
$$ \frac{mx(t)+MX(t)}{m+M} = \frac{ mx(0)+MX(0) }{m+M} + \frac{ mv_x(0)+MV(0) }{m+M}t $$
となり、重心 $x_G(t) = \frac{mx(t)+MX(t)}{m+M}$は等速直線運動となります。
係数は$x_G(0) = \frac{ mx(0)+MX(0) }{m+M} $
及び $v_G(0) = \frac{ mv_x(0)+MV(0) }{m+M} $
となるため、
$ x_G(t) = x_G(0) + v_G(0)t $
と表されます。
これは外力を受けない一物体の運動と全く同じですね。