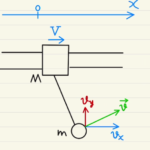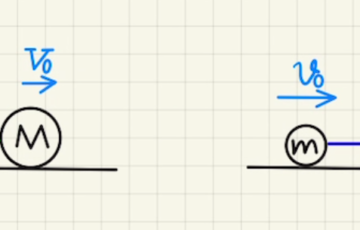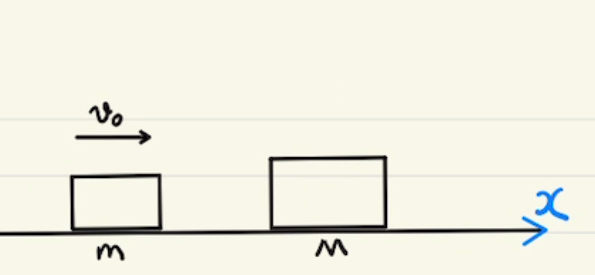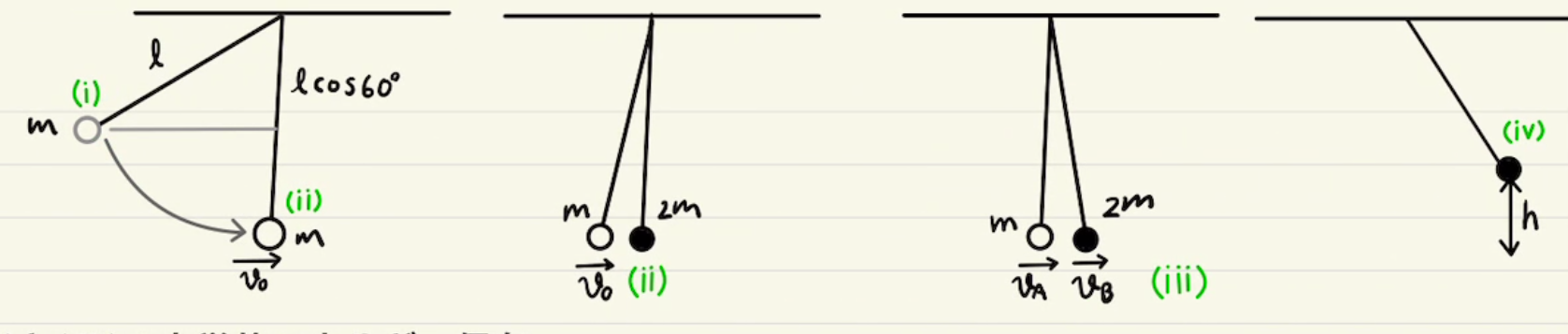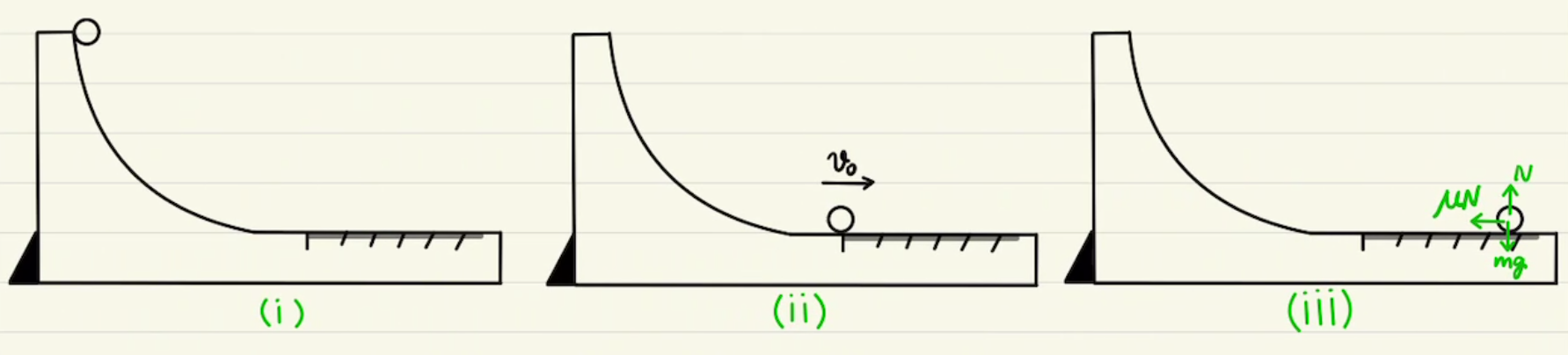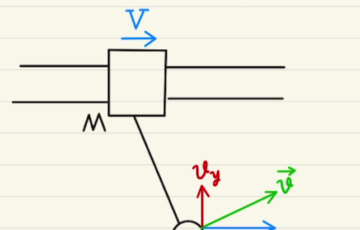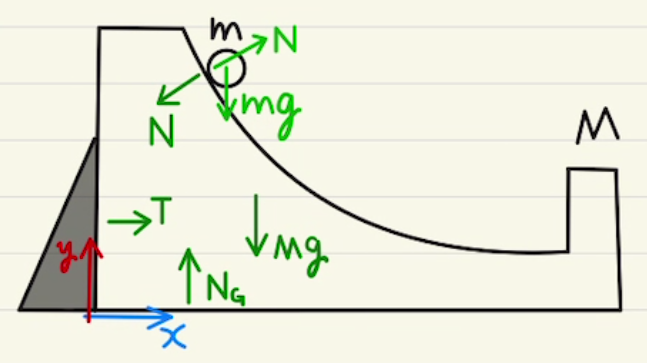
(1)~(3)まではストッパーがついている状態となっています。
そのため衝突するまでは台が動かず小球だけ考えればいいことになります。
その間ストッパーから $x$方向に力を受けているため、$x$方向に運動量は保存しません。
衝突後にストッパーから離れてからは$x$方向に運動量が保存します。
(1)
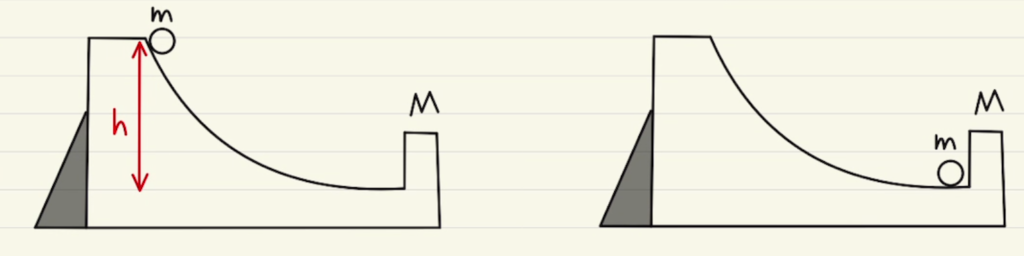
エネルギー保存則より
$mgh=\frac{1}{2}mv_0^2$
よって、$v_0=\sqrt{2gh}$
(2)
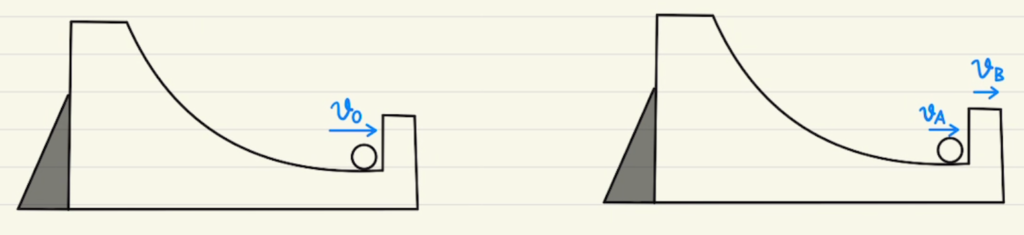
衝突前後の運動量保存の式は
運動量保存:$mv_0=mv_A+mv_B$
反発係数:$v_B-v_A=-1(o-v_0)$
より
\begin{align}
\begin{cases}
v_A = \frac{M-m}{M+m}\sqrt{2gh} \\
v_B = \frac{2m}{M+m}\sqrt{2gh}
\end{cases}
\end{align}
(3)

最高点に着いたとき、小球は台に対して静止します。
つまり小球と台の速度が同じになるのでそれを$v_2$とすると
運動量保存:$ mv_0=(m+M)v_2 $
より $v_2= \frac{M-m}{M+m}v_0$
エネルギー保存則: $ \frac{1}{2}mv_A^2+ \frac{1}{2}mv_B^2 = \frac{1}{2}(m+M)v_2^2+ mgh_2 $
よって
$h_2=\frac{1}{2g} \frac{M}{m+M}v_0^2= \frac{M}{m+M} h$
補足
今回の場合、弾性衝突であるため、最初から最後までエネルギー保存則が成り立ちます。
そのため、下のように書いてしまってもかまいません。
エネルギー保存則: $ mgh = \frac{1}{2}(m+M)v_2^2+ mgh_2 $
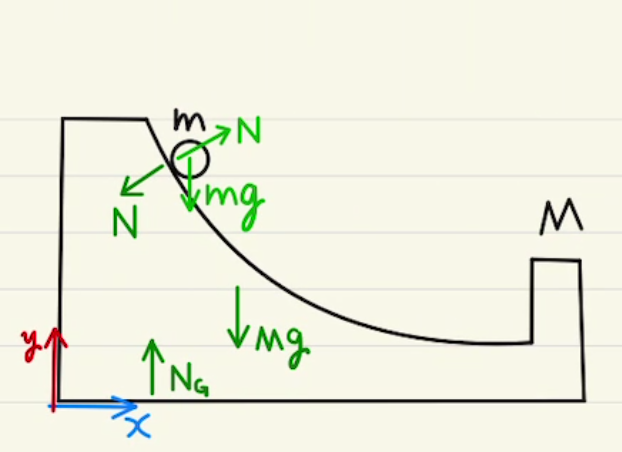
(4)(5)はストッパーがないため、$x$方向の外力が働かず、 $x$方向の運動量が保存します。
外部とのエネルギーのやりとりは衝突のみですが、今回は弾性衝突であるためエネルギー消失は$0$として扱えます。
(4)

\begin{align}
\begin{cases}
運動量保存: m×0+ M×0 = mv_a+M_b \\
エネルギー保存: mgh = \frac{1}{2}v_a^2+ \frac{1}{2}v_b^2
\end{cases}
\end{align}
の連立方程式からそれぞれの速度は
\begin{align}
\begin{cases}
v_a &=& -\sqrt{\frac{2M}{m+M}gh} \\
v_b &=& \sqrt{\frac{2m^2}{M(m+M)}gh}
\end{cases}
\end{align}
となります。(速さはこれの絶対値)
(5)
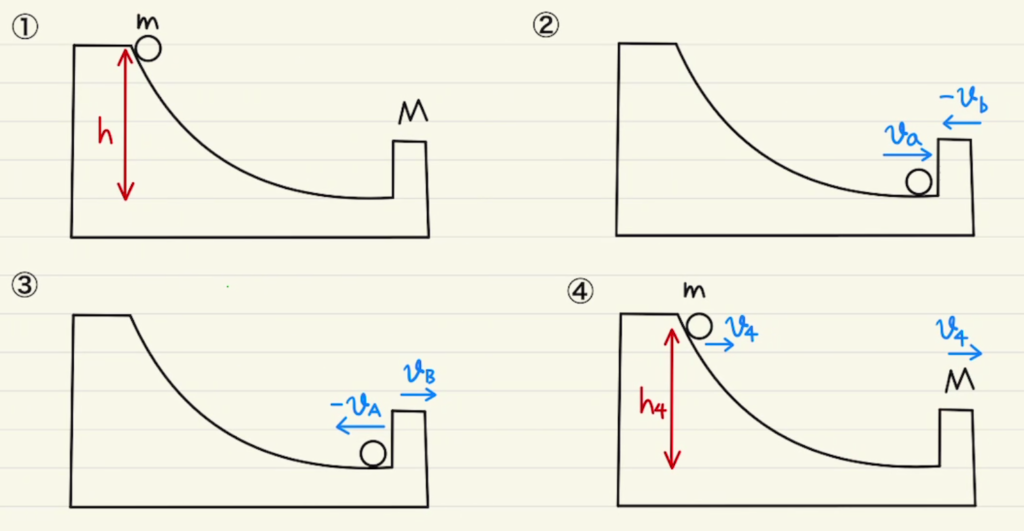
弾性衝突であるため、最初から最後までエネルギー保存則が成り立ちます。
最後は一体になって動くため、その速度を$v_4$、高さを$h_4$とする。
①と④の運動量保存より、
\begin{align}
\begin{cases}
運動量保存: (m+ M)×0 = (m+ M)v_4 \\
エネルギー保存: mgh = mgh_4 + (m+M)v_4^2
\end{cases}
\end{align}
よって$v_4=0$、$h_4=h$となります。
つまり完全に元の状態に戻ります。
補足
弾性衝突ではない場合、 運動量保存は同じく
$(m+ M)×0 = (m+ M)v_4 $
より、$ v_4 =0$となります。
衝突係数をeとすると、衝突によるエネルギー損失$ΔE$は相対運動エネルギーの変化に等しく
$ΔE=\frac{1}{2} \frac{mM}{m+M}(1-e^2)(v_b-v_a) $
となるため、エネルギー保存は
$mgh = mgh_4 + (m+M)v_4^2- ΔE $
より、
$h_4=h-\frac{ ΔE }{mg}=h- \frac{ 1 }{2g}(1-e^2) \sqrt{\frac{2M}{m+M}gh} $
となります。