解答欄


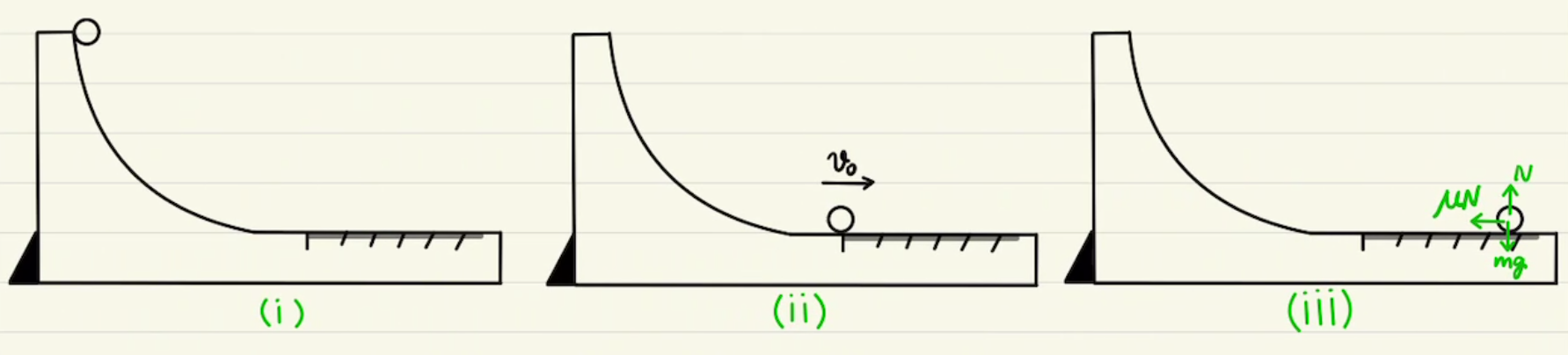
典型的な糸につるした物体の問題。 力学的エネルギーが保存する場面と運動量が保存する場面をそれぞれ考えます。
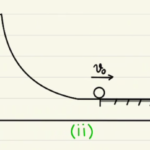
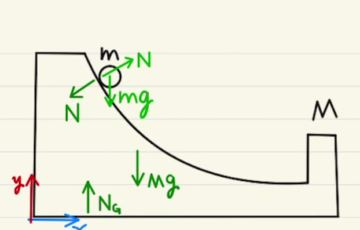
(ⅰ)から(ⅱ)は外部に重力以外は物体に仕事をしないため、力学的エネルギーが保存します。
(重力がした仕事は位置エネルギーの損失としておきかえられているため、運動エネルギーと位置エネルギーの合計は保存します。)
ちなみに張力$T$は常に速度の垂直方向にしか働かないため、仕事はしません。
逆に運動量は保存しません。
重力と張力の合力が力積をもたらし運動量を変化させているからです。
事実、物体は加速しています。
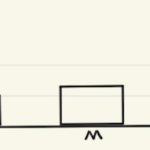
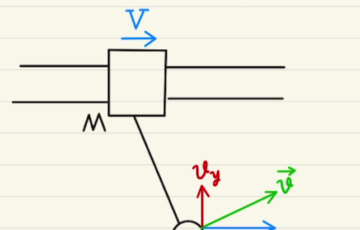
一方で(ⅱ)から(ⅲ)の衝突では二物体の運動量の合計が保存します。
衝突は一瞬であるため、 重力と張力による力積は無視できるからです。
(逆に衝突による二物体間が有限な力積のやりとりでかかった力は理論的には無限大と解釈できるでしょう。実際には0秒ということはないので無限ではないですが、非常に大きな力がかかっています。)
逆に力学的エネルギーは必ずしも保存しません。保存するのは$e=1$の時だけです。
それ以外の時は、 衝突時に音や熱としてエネルギーがその外に逃げます。
これらを踏まえて解いていきましょう。
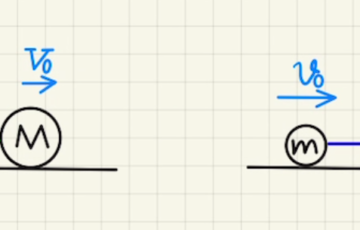
(1)と(2)(3)で反発係数が異なる場合を想定をしているため、一般的に反発係数eのときの衝突後の速度を求めています。
(1) は反発係数がわかっているケース、 (2)(3) では衝突後の片方の速度がわかっているケースとなります。
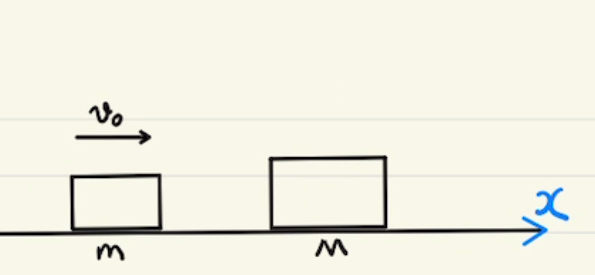
(4)に関してですが、本来は反発係数と連立するところなのですが、反発係数0の場合は二つの物体の速度は同じになるので、式を立てるまでもありません。
反発係数0の場合衝突後に一体となって動きます。
このとき、一体になった質量が$n$倍になった場合、運動エネルギーは$\frac{1}{n}$となります。