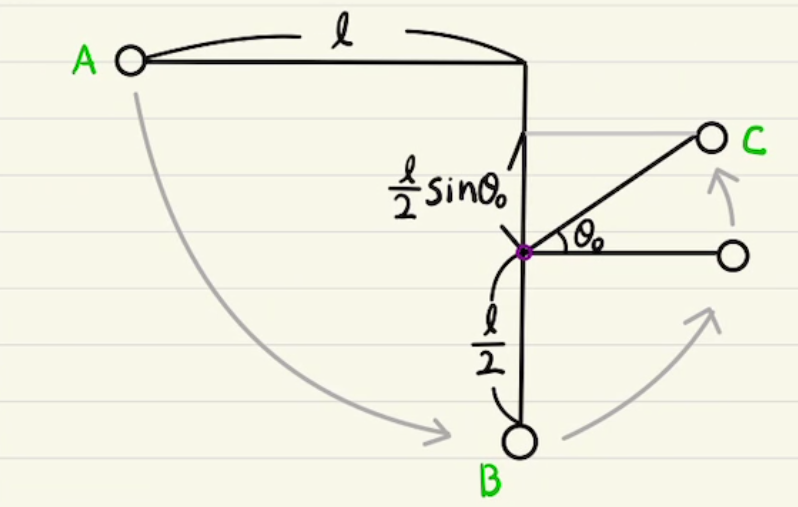
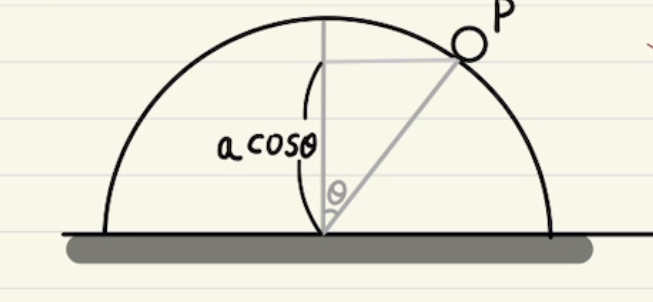
円運動では等速円運動と非等速円運動に分けて説明していきます。
その前に角度について一つ話しておきます。
1秒間に何[rad]の角度回転するかを角速度と言います。角速度$ω=2π$なら$1$秒に$1$回転、$ω=π$なら1秒に半回転といった形になります。
角度と位置、角速度と速度、各加速度と加速度がそれぞれ対応しています。
すなわち角度$θ$を時間で微分すると角速度$ω$となり、 角速度$ω$を時間で微分すると角加速度$\dot{ω}$となります。
等速円運動では、角速度が一定となり、非等速円運動では角速度が一定ではなくなります。
等速円運動
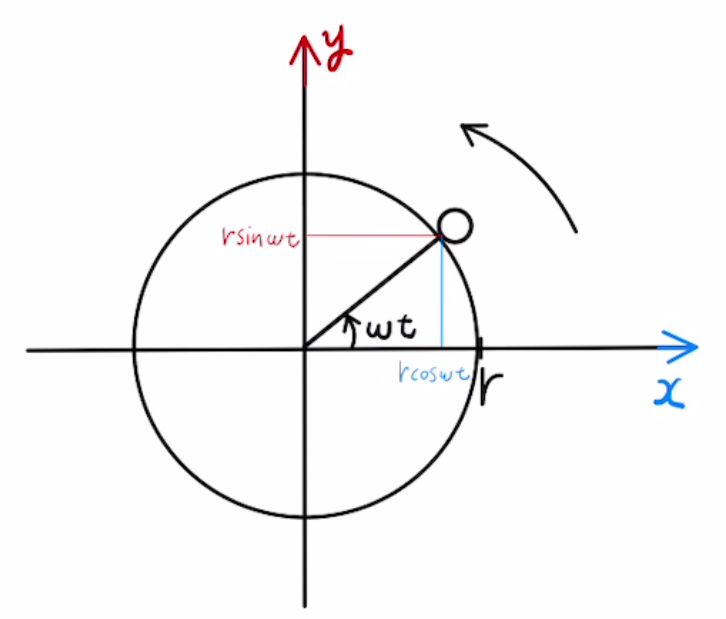
円の中心から長さ$r$の紐で等速で円運動させること考えます。
等速で円運動するときは角速度$ω$が一定なので定数として扱っていきます。
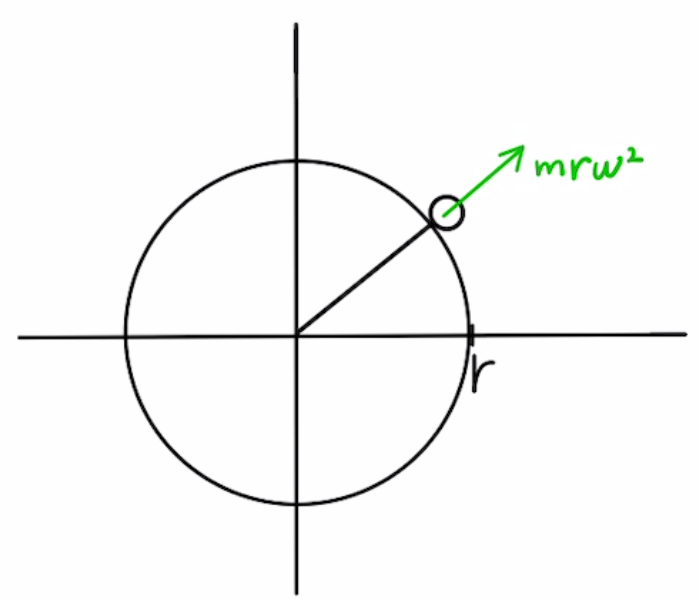
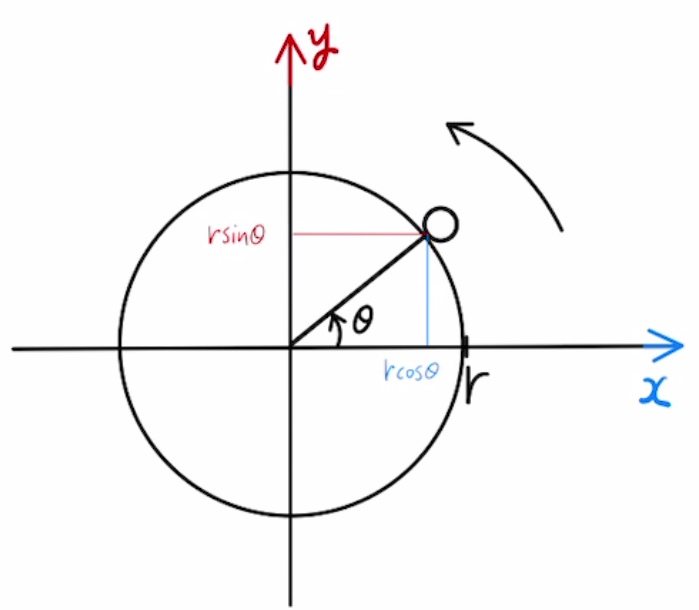
また、等速なので図の角度は $ωt$と置けます。
そのため、物体の位置$\vec{x}$はこう表せます。
$$\vec{x} = \begin{bmatrix} x \\ y \end{bmatrix} = r\begin{bmatrix} \cos{ωt} \\ \sin{ωt} \end{bmatrix} $$
この式を時間で微分すると
$$\vec{v} = rω\begin{bmatrix} -\sin{ωt} \\ \cos{ωt} \end{bmatrix} $$
これが速度の式となり、図に書き込むと円の接線方向だということがわかります。
速さは絶対値を取って$| \vec{v} | = rω $となります。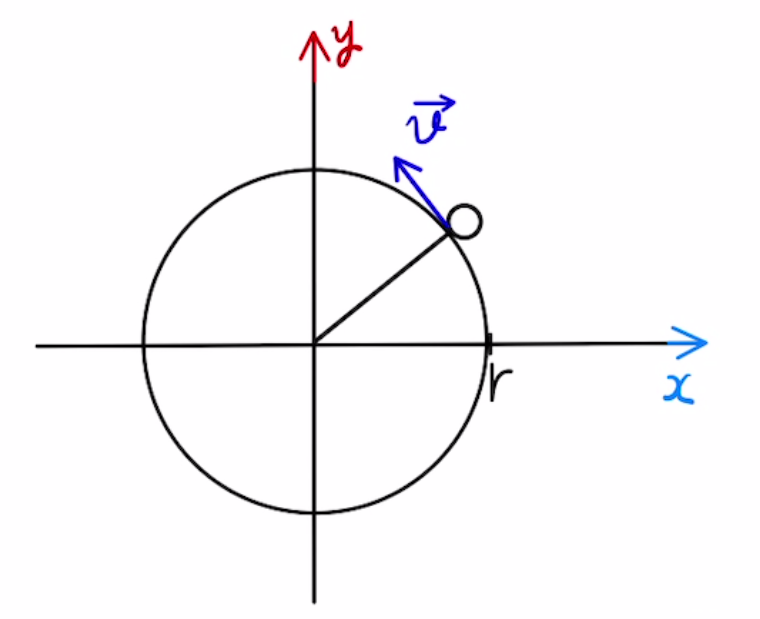
また、速さを時間で微分すると
$$\vec{a} = -rω^2\begin{bmatrix} \cos{ωt} \\ \sin{ωt} \end{bmatrix} $$
となります。
これを運動方程式$m\vec{a}=\vec{f}$に照らし合わせてみると
$$ -mrω^2\begin{bmatrix} \cos{ωt} \\ \sin{ωt} \end{bmatrix} = \vec{f} $$
等速で円運動を行うには円の中央に向かって$mrω^2$の力をかけなければならないことがわかりました。
これを向心力と言います。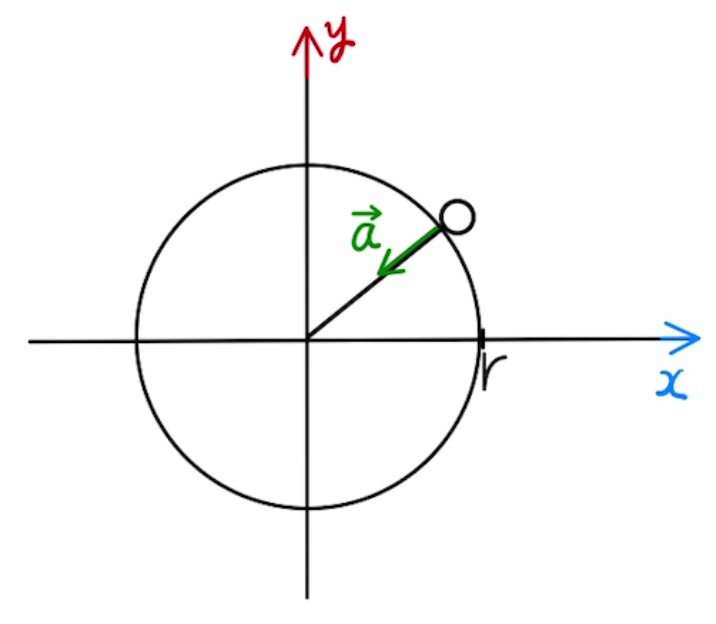
慣性力の時と同様、回転している物体視点から見てみるとどうなるでしょうか。
運動方程式$m\vec{a}=\vec{f}$ を $\vec{0}=\vec{f}- m\vec{a} $と書き換えられます。
すなわち、
$$ \vec{0} = \vec{f} + mrω^2\begin{bmatrix} \cos{ωt} \\ \sin{ωt} \end{bmatrix} $$
が成り立ちます。
この円の中心から外側方向に働く慣性力$f_c = mrω^2$を遠心力と呼びます。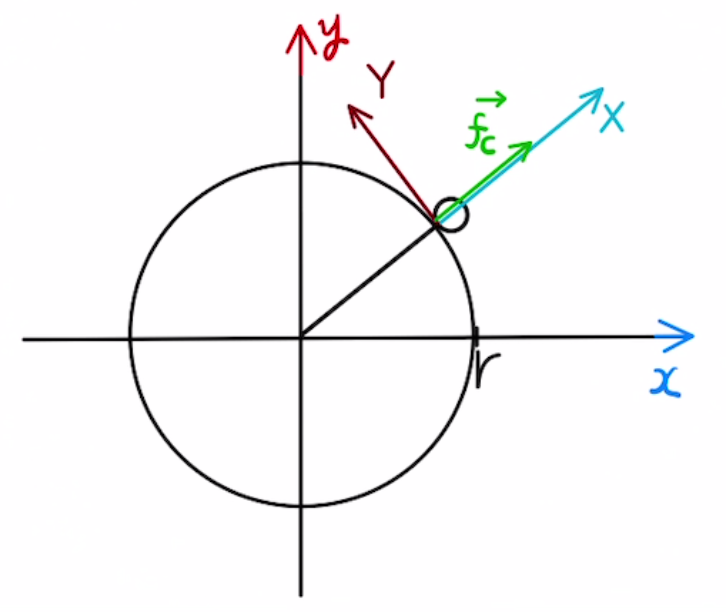
等速円運動では、この遠心力を含めた力のつり合いを考えていくことになります。
なお、$v=rω$から 遠心力$f_c = mrω^2= m\frac{v^2}{r}$で扱うこともあります。
非等速円運動
円運動が等速でない場合は$ω$は一定ではなく$θ=ωt$とはおけないので、 $θ$を時間微分すると$ω$となる事実を使います。
まず物体の位置は
$$\vec{x} = r\begin{bmatrix} \cos{θ} \\ \sin{θ} \end{bmatrix} $$
となります。
これを合成関数の微分を使って時間微分すると
$$\vec{v} = rω\begin{bmatrix} -\sin{ θ } \\ \cos{ θ } \end{bmatrix} $$
ここまでは等速円運動と変わりませんね。
さらにこれを時間で微分します。
$$\vec{a} = -rω^2\begin{bmatrix} \cos{ θ } \\ \sin{ θ } \end{bmatrix} + r\dot{ω}\begin{bmatrix} -\sin{ θ } \\ +\cos{ θ } \end{bmatrix} $$ 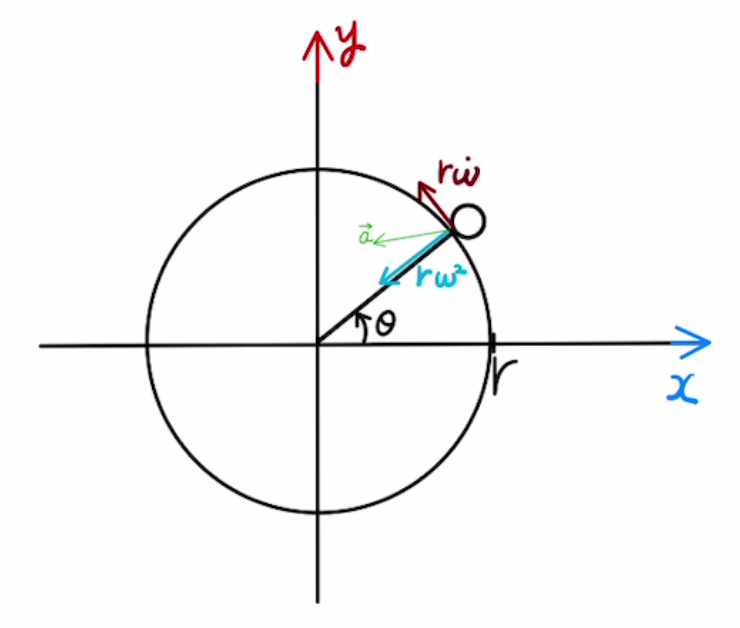
先ほどと同様に遠心力を求めると
$$\vec{f_c} = mrω^2\begin{bmatrix} \cos{ θ } \\ \sin{ θ } \end{bmatrix} – mr\dot{ω}\begin{bmatrix} -\sin{ θ } \\ \cos{ θ } \end{bmatrix} $$
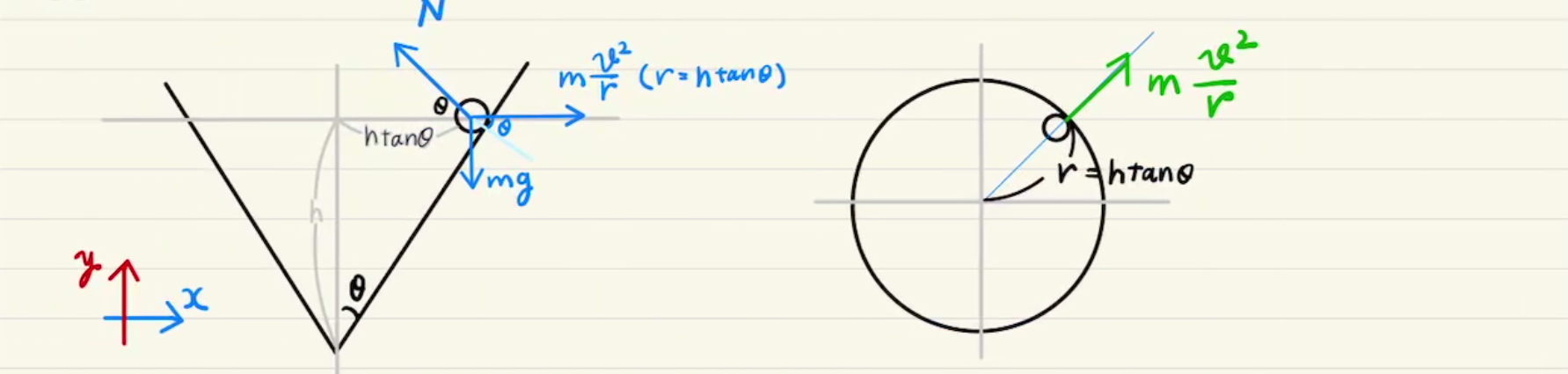
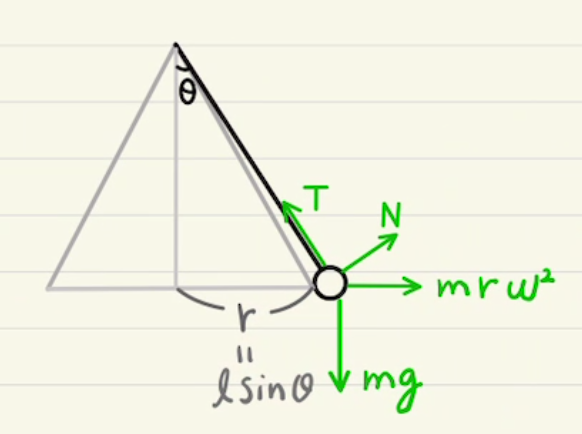
この遠心力を$X,Y$方向に分解すると、図のように力を書き込めます。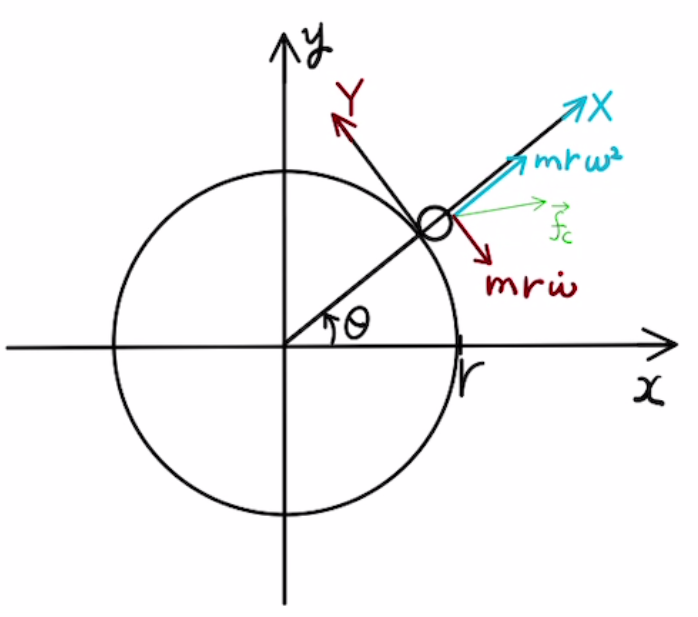
すなわち、図の$X$方向と$Y$方向で力のつり合いが考えられます。
$Y$方向に関しては各加速度が含まれるので、力のつり合いをみることはほとんどありません。
$X$方向の力のつり合いは等速円運動と変わらないので、 X方向の力のつり合いのみ見ていくのが一般的です。
まとめ
・回っている物体視点だと、等速円運動と非等速円運動のどちらも円の中心から外向きに向かって$f_c= mrω^2 = m\frac{v^2}{r}$の遠心力が働いているように見える。
・等速円運動の場合、接線方向には慣性力は働かない。非等速円運動 では $mr\dot{ω}$だけ接線方向(速度と反対向き)に慣性力が働く。
・ほとんどの場合で$X$方向(円の向心方向)のつり合いしか見ない。