解答欄
解説
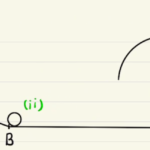
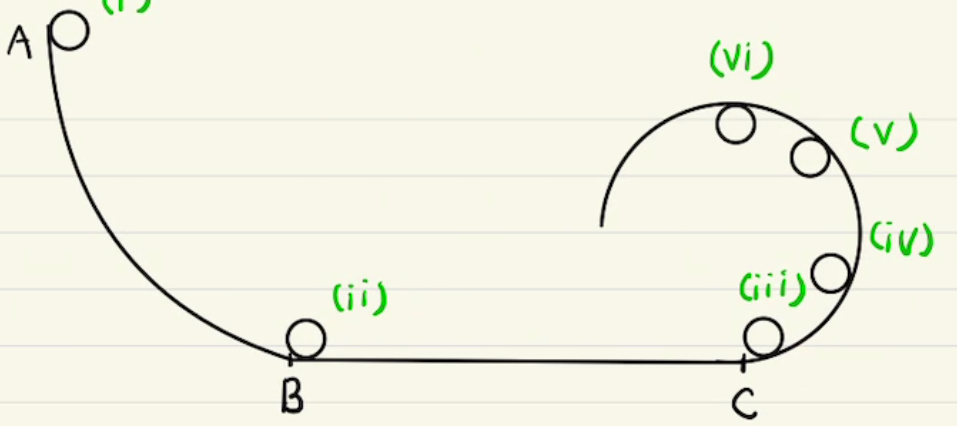
重力によって速さが変わっていくため、非等速の円運動となります。
各位置での速度はエネルギー保存則から求めることができます。
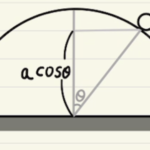
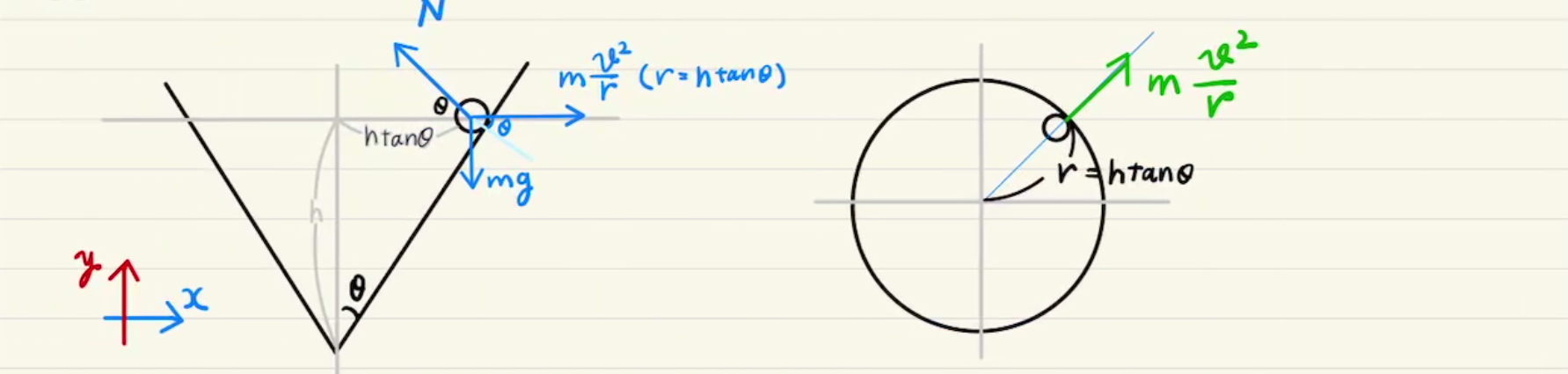
速度を求めることができれば遠心力m\frac{v^2}{r}を求めることもできます。
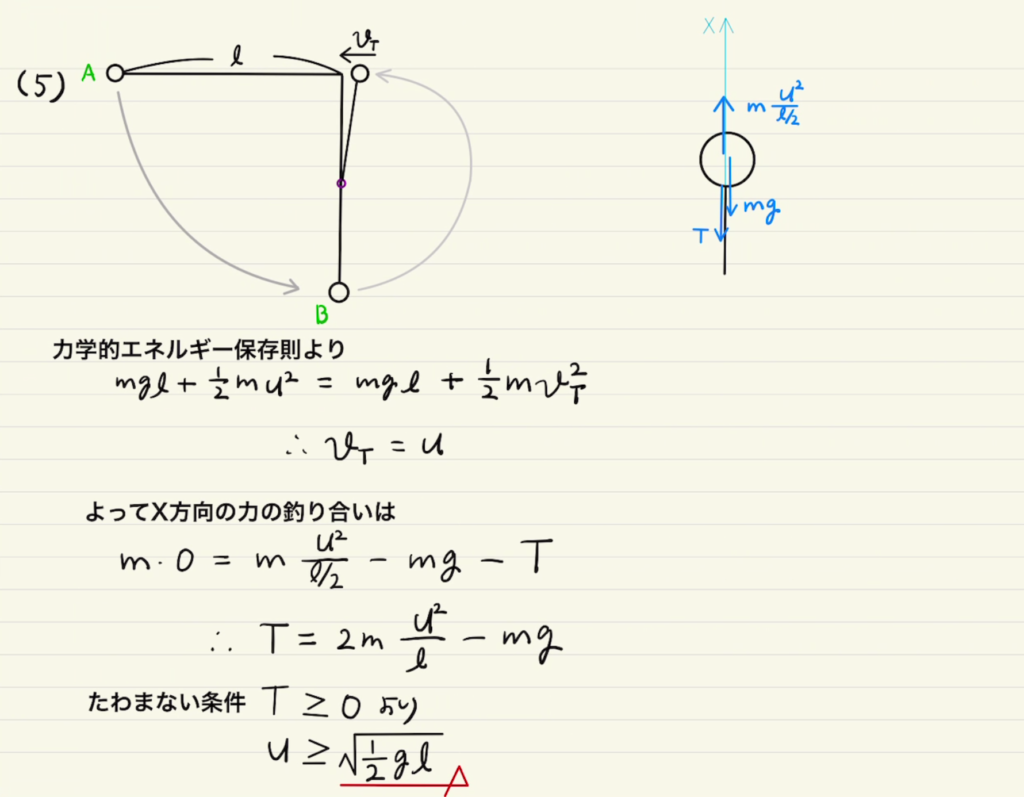
非等速の円運動での力のつり合いは円の向心方向($X$方向)だけ見ることができます。
(垂直方向(速度方向)の力のつり合いは角加速度が含まれるため、計算するのが困難です。)
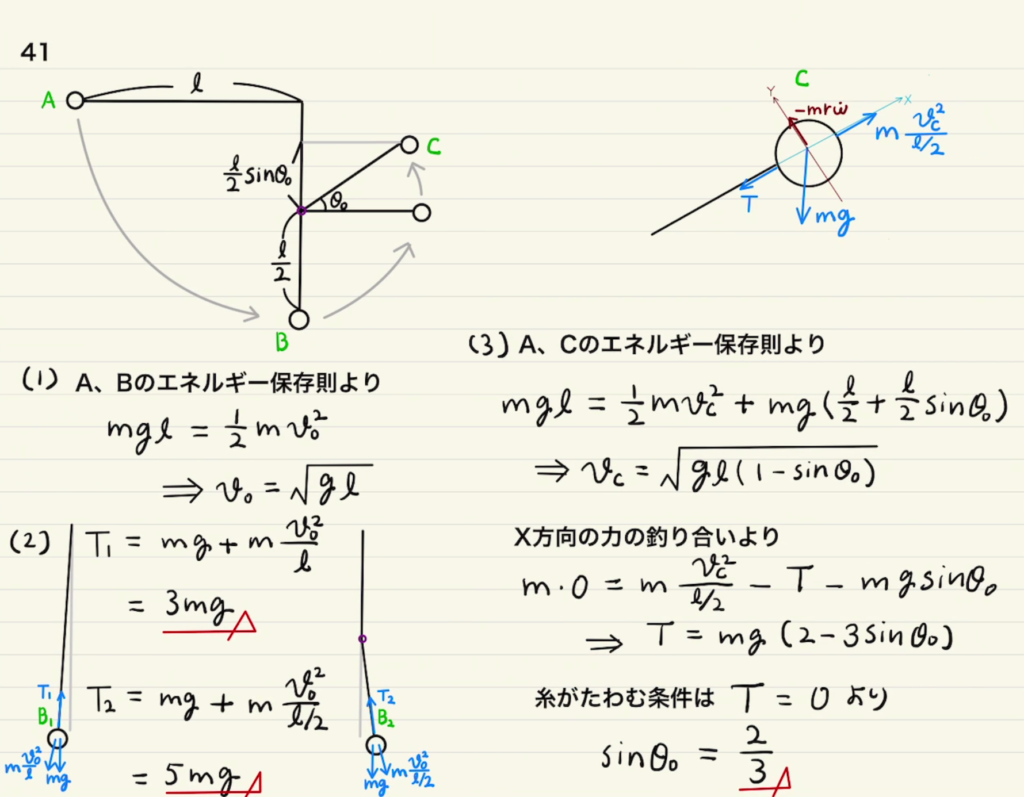
(2)円運動の遠心力は円の半径によって変化するため、糸がPにひっかかる前と後とでは遠心力が異なります。
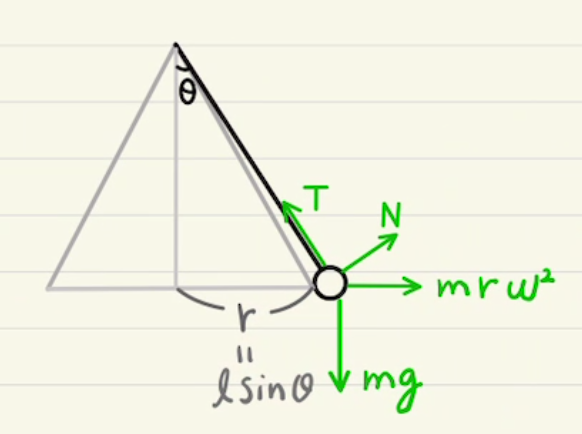
(3)円運動中は糸の張力、重力、遠心力が円の向心方向でつり合っていればよく、そのつり合いの式から張力$T$が求まります。
ただし、今回は遠心力を求めるために速度を求めなければならないため、また力学的エネルギー保存を使います。
糸がたわむのは張力$T$が0となるときです。
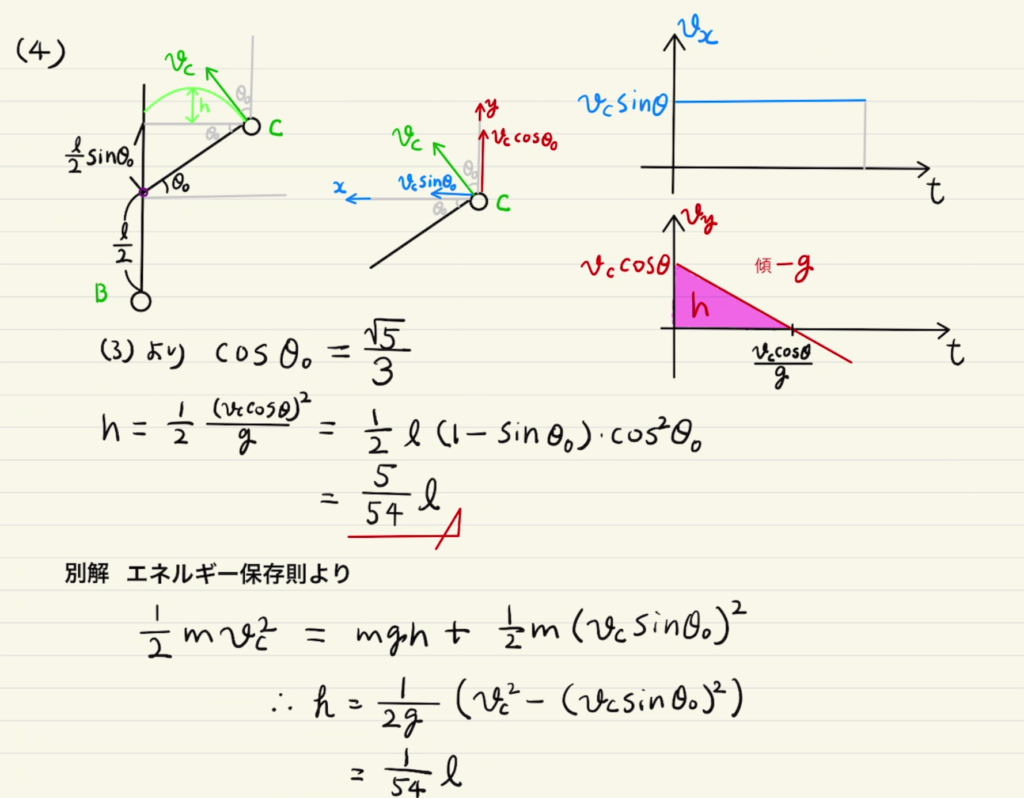
(4)ここではうって変わって放物運動の話となります。
速さも方向もわかっているため、少し面倒ですが計算するだけとなります。
念のためv-tグラフも描いておくといいでしょう。
頂点での速さは$v_c$の$y$成分と同じになることを考えれば力学的エネルギー保存も使うことができます。