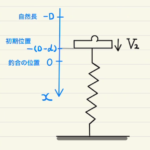
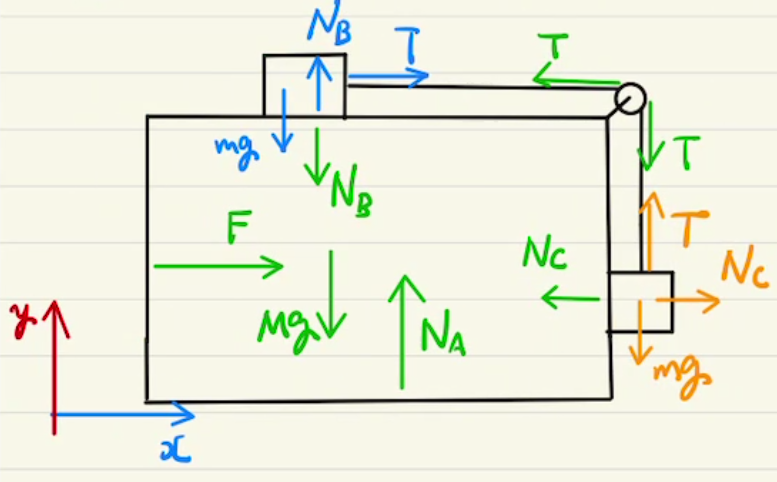
解答欄
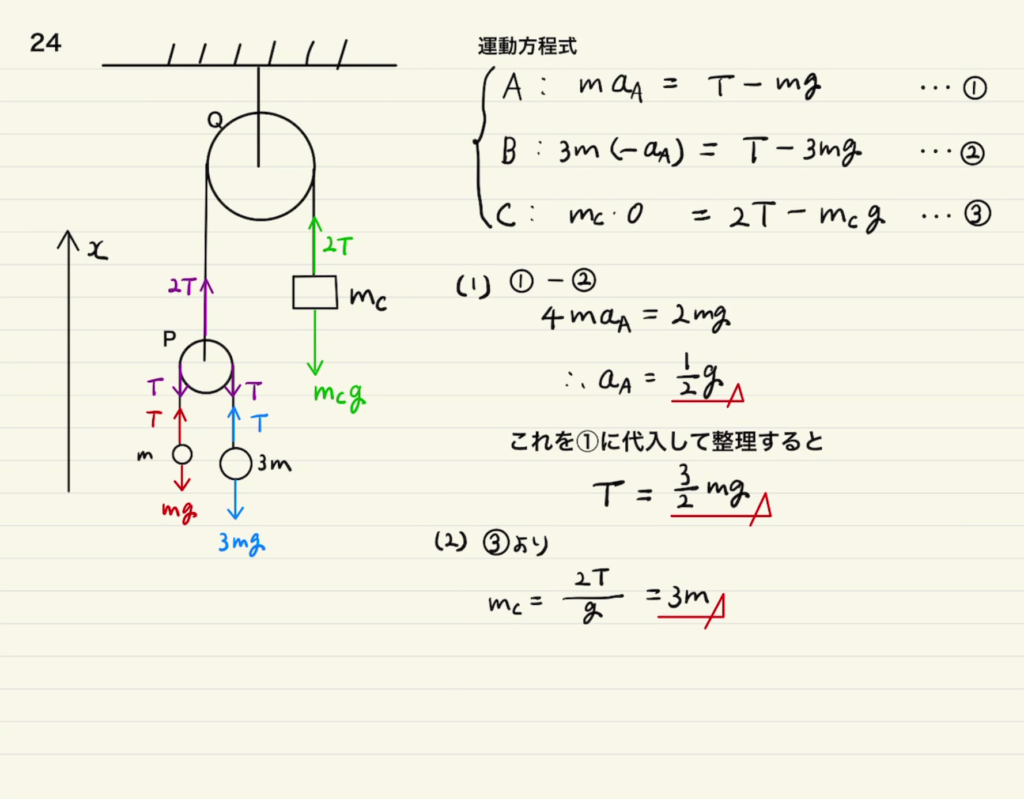
こちらの方が簡単なので試験ならこちらをお勧めします。
解説
慣性力の超有名な難問題です。
(1)(2)までは普通の力のつり合いとして解けると思います。
問題は(3)(4)です。
他の慣性力の問題と同じく外部から見た運動方程式を立てるやりかたと、内部(今回は$Q$視点)で解く方法の二つが考えられます。
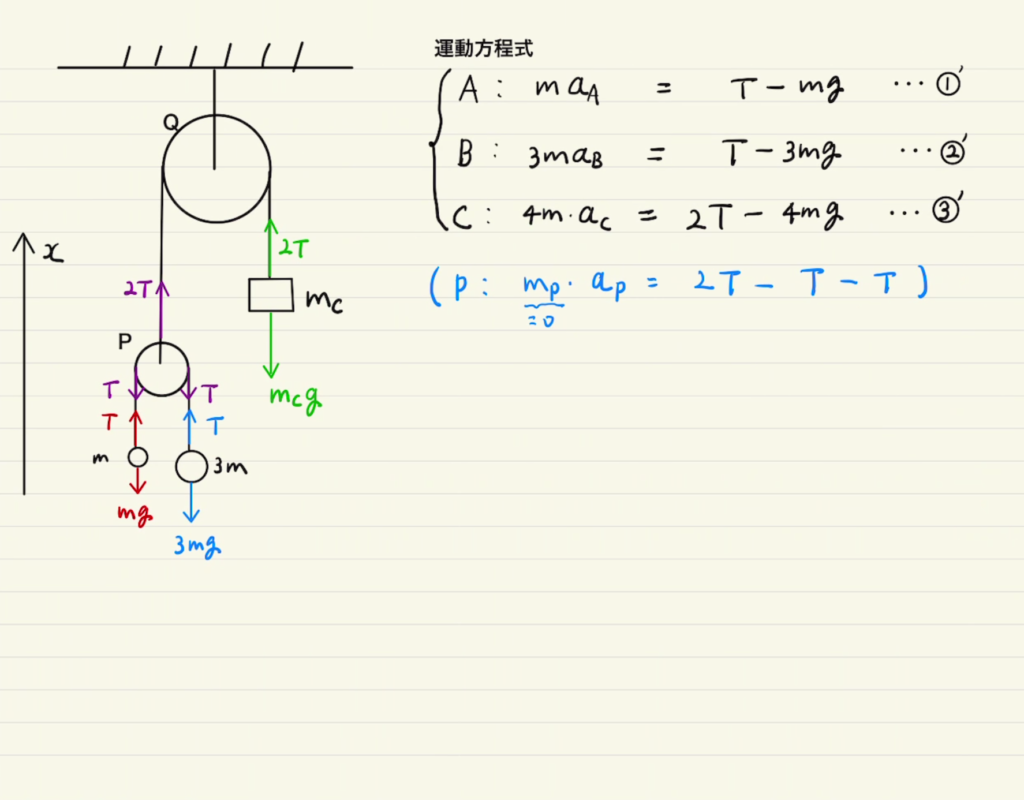
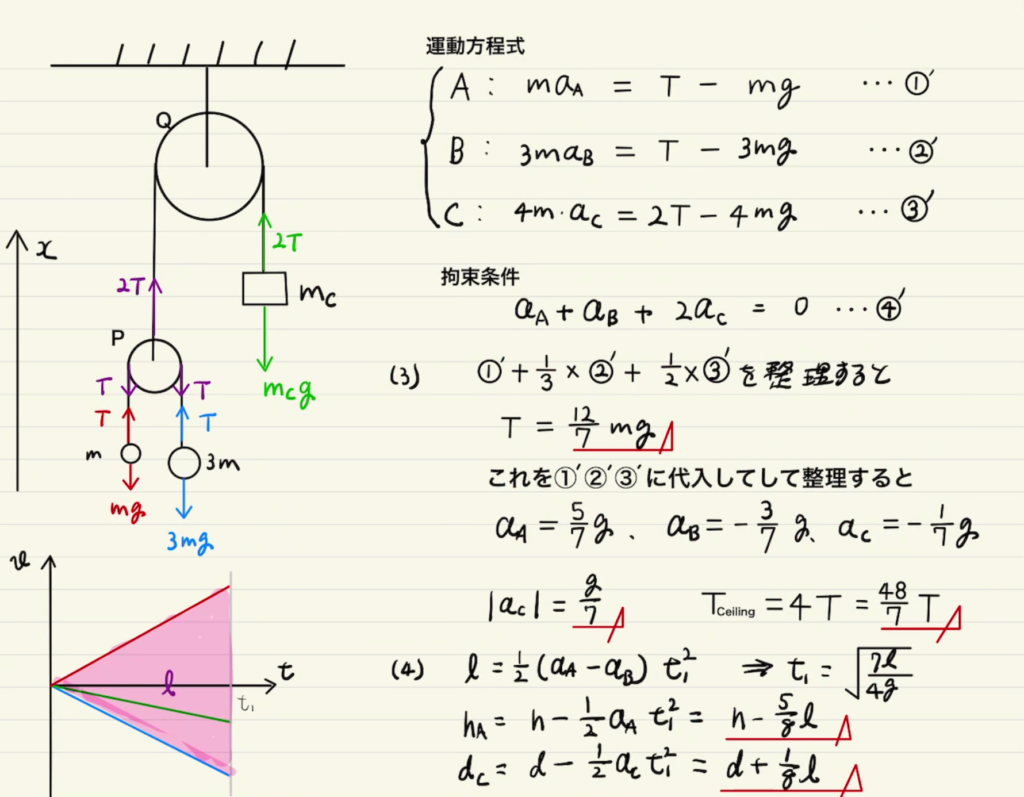
・まず、外部から見た運動方程式から。
$A,B,C$の加速度をそれぞれ設定し、運動方程式①’②’③’を立てましたが、一つ問題が…。
三つの式に対して未知数が4個あります。つまりもう一つ式が必要になります。
ここで考えなければならないのが紐による動きの制限です。
滑車一つの問題を思い出してみましょう。
左は上方向に加速度$a$で動くなら、右は下方向に加速度$a$で動くはずです。
これを拘束条件と言います。
拘束条件のおかげで加速度の変数は一つで済みました。
今回もその条件を考えていきます。
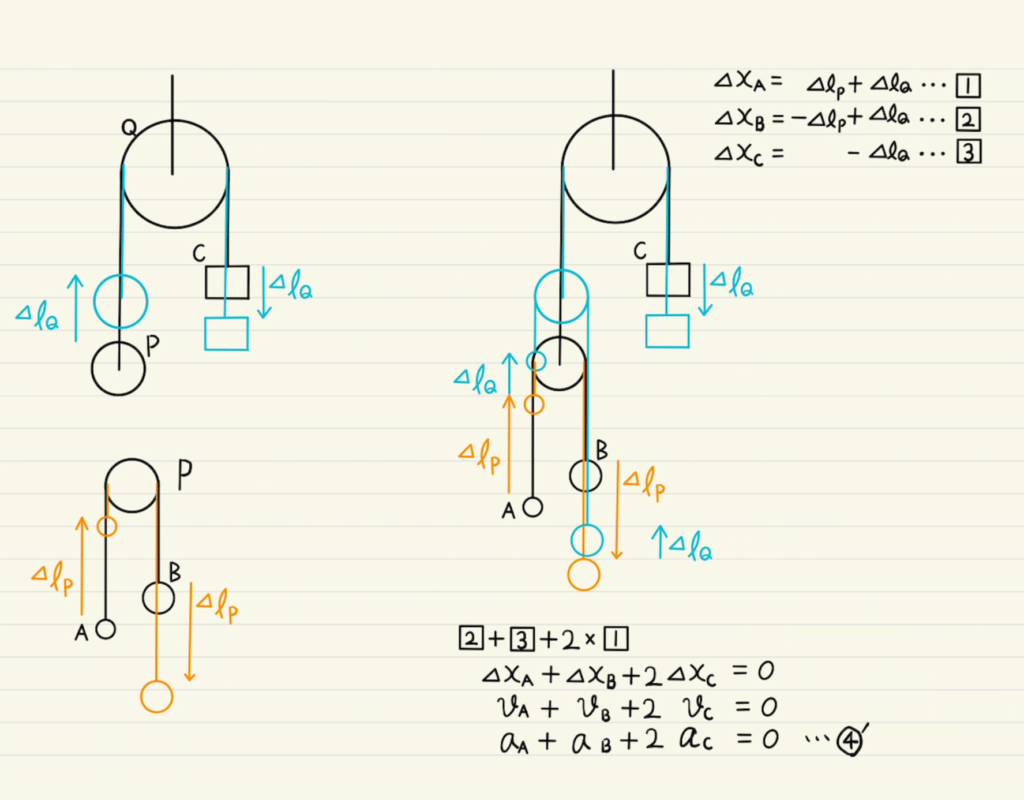
滑車一つの場合を考えると、左右の物体は同じ紐にぶら下がっており、左が上にl動けば右は下に同じだけの距離動くことになります。この変位を二回時間微分すれば加速度になるという寸法です。
同じような考え方を二つの滑車で見てみたのが三枚目の画像。$Q$にかかっている紐が$Δl_Q$動き、$P$にかかっている紐が$Δl_P$だけ動いたとすると、$A,B,C$の変位もこの二つで表せます。
(二つの新しく用意した変数を使って、三つの等式を立てられたということは、一つ自由度を下げられたことを意味します。)
実際に $A,B,C$の変位 だけを使った式が導けました。今回は運動方程式で加速度を知りたいので二回時間微分します。
これを拘束条件④’とすることで4個の式が作れました。
あとは未知数を求めるだけです。
このやり方の場合、外部から見たA,B,Cの加速度をそのまま求められるため、(4)もスムーズに答えられるのではないでしょうか。
(1⃣2⃣3⃣の二回時間微分して$a_A$、$a_B$、$a_C$を求め、 ①’②’③’ に直接 代入する方法もある)
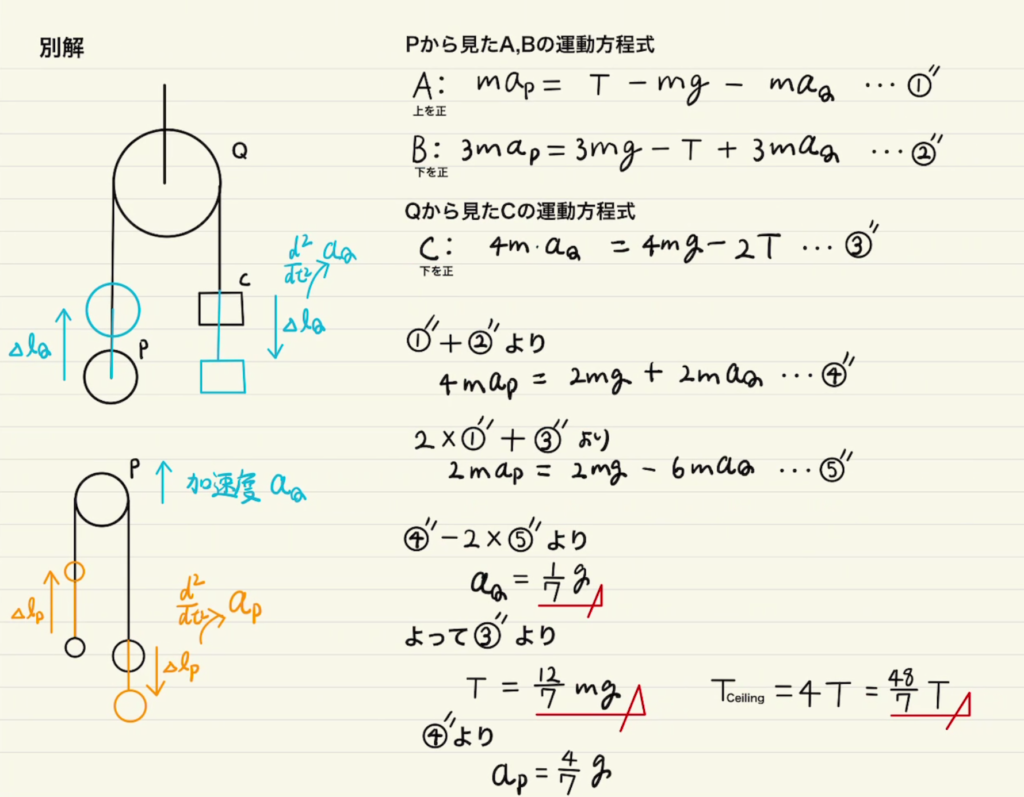
・二つ目は、滑車$Q$から見た運動方程式です。
この場合、紐の変位$Δl_P$ と $Δl_Q$ の2回時間微分である$a_P$と$a_Q$をそのまま運動方程式にいれることができるため、拘束条件がいらなくなります。
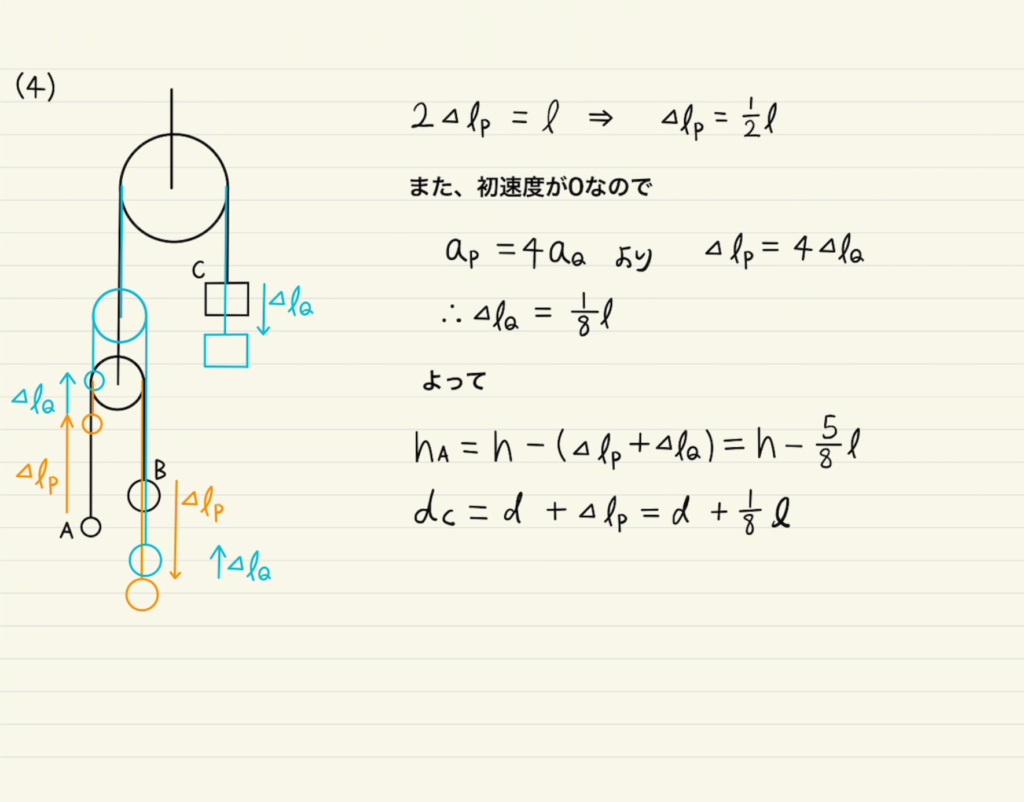
また(4)は$A,B$はどちらも $Δl_Q$ 上昇するためそれによって差はつかず、 $2Δl_P$ 分の上下差ができるためそれを $l$ として解くことができます。加速度の比から$Δl_Q$もすぐ求まります。
どちらの解き方も見ておくべきでしょうが、今回は二つ目の慣性力をのやり方が圧倒的に楽ですね。
滑車の問題では、滑車一つにつき紐の変位$Δl_n$を設定してやれば、その加速度$Δa_n$で運動方程式を立てればほとんどの問題は解けるようになります。
滑車で注目すべき点は変数としておく加速度の基準を、(ⅰ)外から見た物体の動きとするのか (ⅱ)糸の動きとするするのか になりますね。