コンデンサーから電荷が外に流れていくときのどのように電気量が減っていくかを見ていきます。
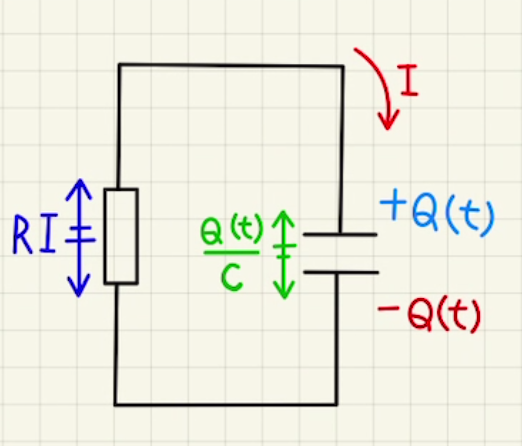
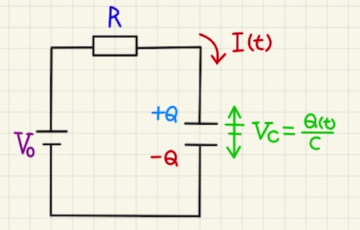
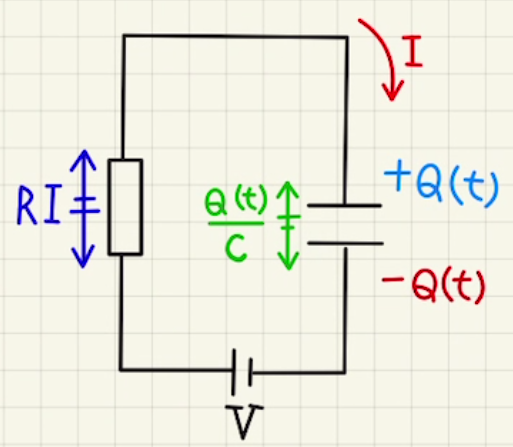
上図のような抵抗とコンデンサーだけの回路の場合の時間変化がどうなるかを見ていきましょう。
結論から言えば、電荷や電流は指数関数として減少していきます。(一定時間たつと半分、同じ時間たつとさらに半分…といった減少のしかたです。)
それを数式で微分方程式を用いて示していきます。
とある時刻のコンデンサーにたまった電荷を$Q(t)$、時計まわりに流れる電流を$I_t$、コンデンサーの電位差を$V(t)$とします。
電荷や電流はどちらが正か変わることがあるので、一旦どちらかを正として設定する必要があります。
このとき、$I(t)=\frac{dQ(t)}{dt}$が成り立つのは、電流が正の方向に流れた時に電荷が増える方を正としなければいけません。
$Q=CV$の式から$v(t)= \frac{Q(t)}{C} $ となるため、このとき回路の式は
$$\frac{Q(t)}{C}+ RI(t)=0 $$
が成り立ちます。
(どちらも電流が流れる方向と逆方向を正の起電力と設定しているので、一周したときの二つの足し算が0となります。)
よって流れる電流は、右まわりを正とすると
$$ I =-\frac{1}{CR}Q(t)$$
ここで電流は電荷の1秒当たりの移動量で定義されることから
$$I(t)=\frac{dQ(t)}{dt}$$
となるので、これを回路の式に代入すると
$$ \frac{dQ(t)}{dt} =-\frac{1}{CR}Q(t)$$
この微分方程式を解いていくことになります。
この式は電荷がたまっていると、それがどんどん減少していくことを示しており、その電荷が大きいほど減少量も多くなります。
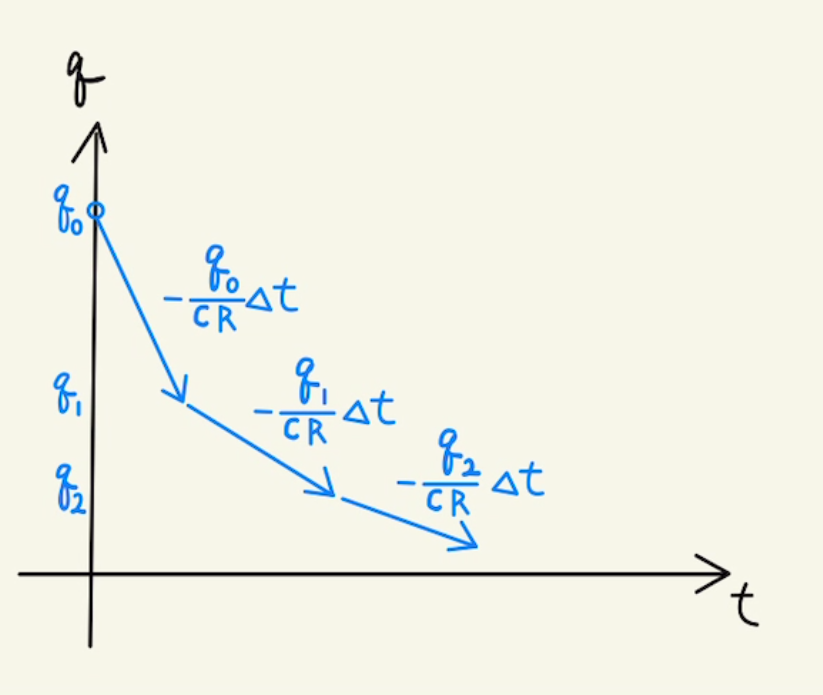
変数分離を使うと
$$ \frac{dQ (t) }{Q (t) } =-\frac{1}{CR}dt$$
となり、この両辺を積分すると、
$$ \log{Q (t) } =-\frac{1}{CR}t + C_0$$
$C_0$は積分定数となります。
ここで両辺を$e^{〇〇}$に入れると
$$ Q(t) = e^{-\frac{1}{CR} t+C_0} $$
$Q_0=e^{ C_0 }$とおくと、
$$ Q(t) = Q_0e^{-\frac{1}{CR} t} $$
積分定数の$Q_0$は最初にたまっていた電荷できまり、
$t=0$を代入すると、
$Q(0) = Q_0$
となることから、$ Q_0$は最初にコンデンサーにたまっていた電荷となります。
電荷を電圧Vで貯めた場合は$ Q_0=CV$ですね。
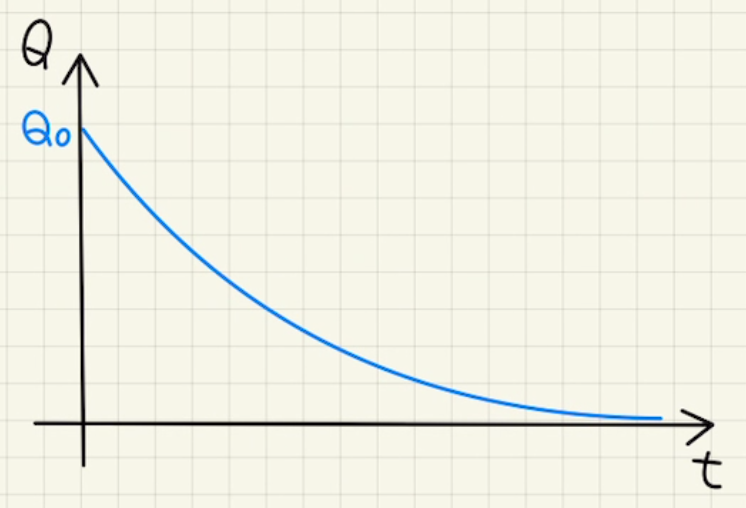
$$Q(t)= Q_0e^{-\frac{1}{CR} t}$$
これが電荷の時間変位とわかりました。
指数の部分が見づらいので、
$Q(t)= Q_0\exp{(-\frac{1}{CR} t)}$
と表記することが多いです。
電流や電圧の時間変化も表すことができ、
$I(t)= \frac{Q(t)}{RC} = \frac{Q_0}{RC} \exp{(-\frac{1}{CR} t)}$
$V(t)= RI(t) = \frac{Q_0}{C} \exp{(-\frac{1}{CR} t)} $
と、どちらも指数関数となります。
抵抗での時間当たりの消費電力は
$$P(t)=RI^2= \frac{Q_0^2}{RC^2} \exp{(-\frac{2}{CR} t)} $$
となり、たくわえた電荷が全てなくなるまでに消費したエネルギーは
$$W=\int_0^∞{P(t)dt}=\left[ -\frac{Q_0^2}{2C} \exp{(-\frac{2}{CR} t)} \right] _0^∞ = \frac{Q_0^2}{2C} $$
と求めることができ、コンデンサーに蓄えられたエネルギー $\frac{Q_0^2}{2C} $ と一致することが確認できました。
同じようにコンデンサーを蓄える場合も計算できます。
回路の方程式は
$$V=\frac{Q(t)}{C}+ RI(t) $$
から
$$ I =-\frac{1}{CR}(Q(t)-CV)$$
ここに$I=\frac{dQ(t)}{dt}$を代入すると
$$ \frac{dQ(t)}{dt} =-\frac{1}{CR}(Q(t)-CV)$$
ここで$q(t)= Q(t)-CV$と置くと
$$ \frac{dq(t)}{dt} =-\frac{1}{CR}q(t)$$
同じように変数分離で解いていくと
$$q(t)= q_0e^{-\frac{1}{CR} t}$$
となることから、 $Q(t)= q(t)+CV$を代入して
$$Q(t)= q_0e^{-\frac{1}{CR} t} + CV$$
最初に電荷が $Q(0)=0$ だったとすれば、$t=0$を代入して、
$Q(0)= q_0+ CV=0$
となるため、$ q_0 =- CV $
よって
$$Q(t)= CV(-e^{-\frac{1}{CR} t} + 1)$$

電流の変化は
$$I(t)= \frac{V}{R}e^{-\frac{1}{CR} t}$$