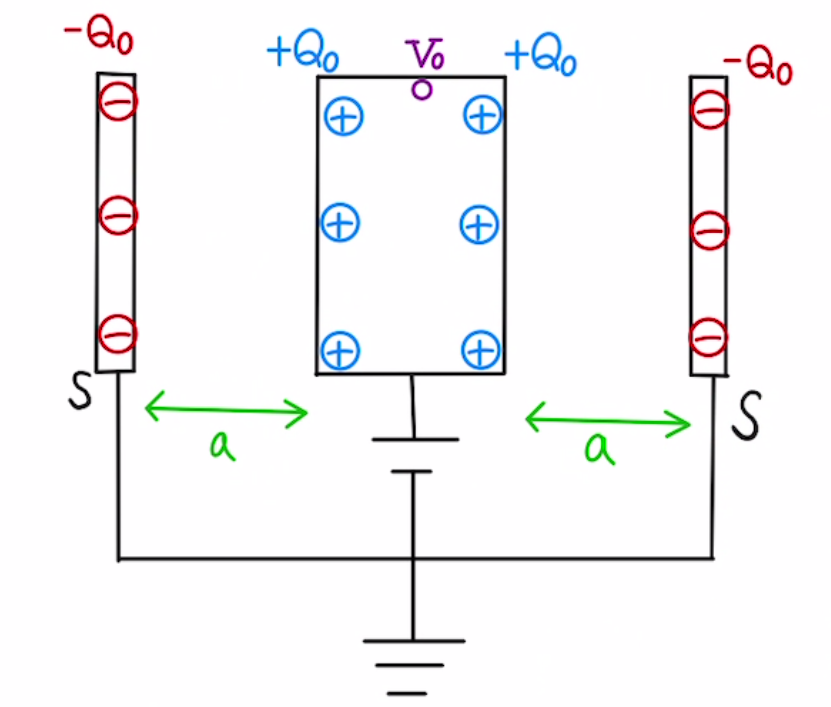
接地されている場所は電位$0$であることに留意します。
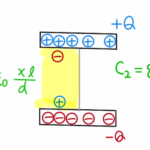
(1)幅、面積が同じため、静電容量は等しくなります。
両端の電位はどちらも$0$で電位差も等しくなり、
どちらも$Q_0=CV_0$となり、合計は2Q_0となります。
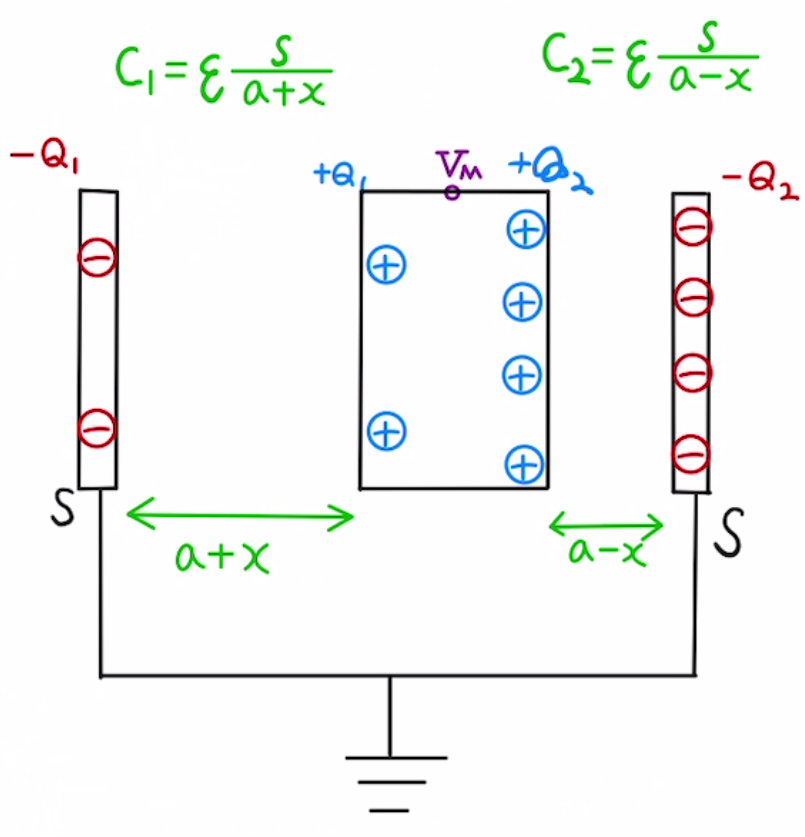
孤立している場合、電荷の出入りはなくなるため、電気量は変化しません。
つまり$Q_1+Q_2=2Q_0$となります。
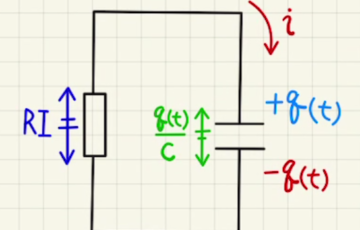
中央の電位が$V_M$となったとすると、上の式に電気容量の定義を代入して
$$ε\frac{S}{a+x}V_M+ ε\frac{S}{a+x}V_M = 2ε\frac{S}{a}V_0 $$
よって
$$V_M = (1-\frac{x^2}{a^2})V_0 $$
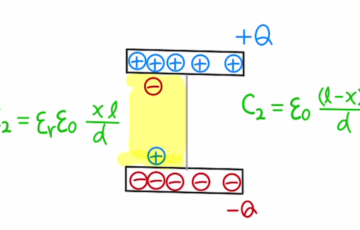
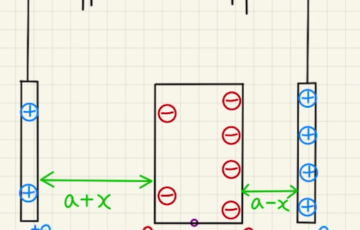
(3)図から
$$-Q_1=- ε\frac{S}{a+x} V_M = – (1-\frac{x}{a})Q_0 $$