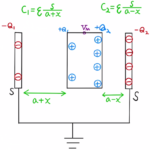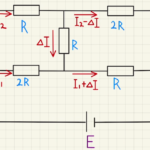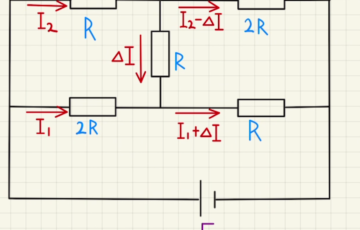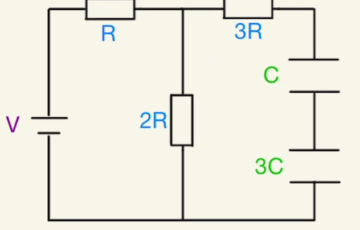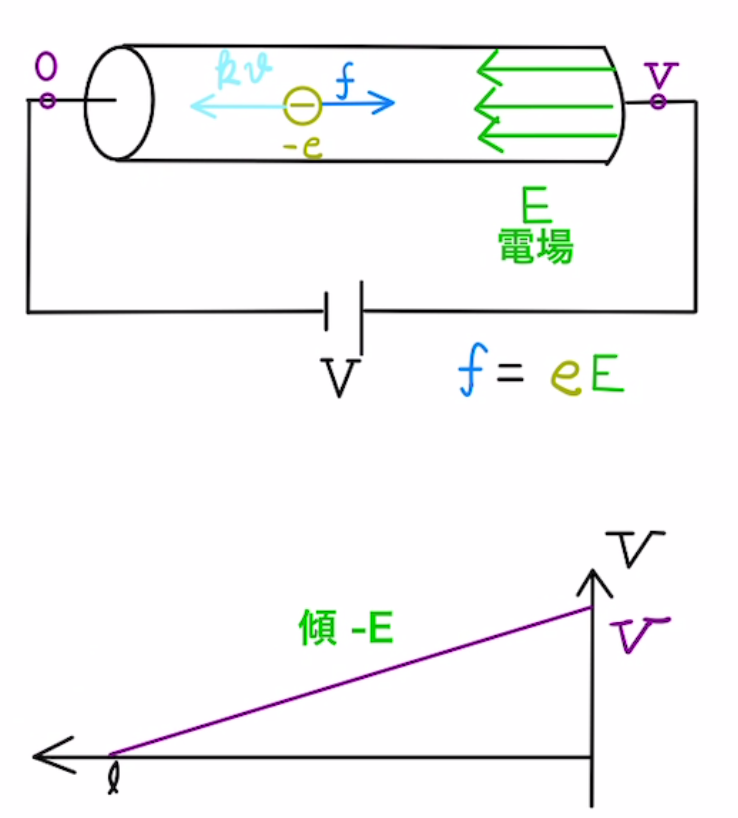
(1)抵抗の右端は電位Vで、左端は電位0となっています。
抵抗の中では均一に電位が下がっていっているとすると、発生している電場は
$$E=\frac{V}{l}$$
となります。
これは電場→重力、電位→位置エネルギーに置き換えてみると理解しやすいでしょう。
(2)電子が電荷$-e$だけ持っているとすると、かかる力の大きさは
$$f=eE=e\frac{V}{l}$$
となります。電荷はマイナスであるため、電場の逆方向である右側に力が働きます。
(3)
空気抵抗の問題と同様、等速度で動いているときは力はつり合っています。
そのため、力のつり合いは
$$kv=e\frac{V}{l}$$
となり、
$$v= \frac{eV}{kl} $$
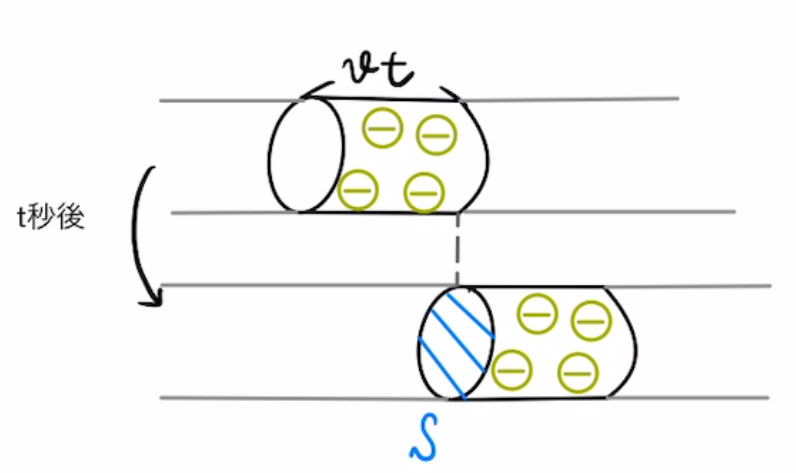
(4)$t$秒間の間に断面を通った電子の数$N$は
$$N=nV=nSvt$$
よって断面を通った電荷$q$は
$$q=eN=enSvt$$
よって電流の定義から
$$I=\frac{dq}{dt}=enSv$$
(5) (3)の式を代入して
$$ I=enSv= enS \frac{eV}{kl} $$
よって抵抗値の定義より
$$R=\frac{V}{I}= \frac{kl}{e^2nS} $$
(6)抵抗率$ρ$は
$$R=ρ\frac{l}{S}$$
と定義されます。
電気抵抗は長いほど大きく、太いほど小さくなります。
この二つに依存しない材質による電気抵抗の大きさが抵抗率となります。
$ρ= \frac{k}{e^2n} $
補足
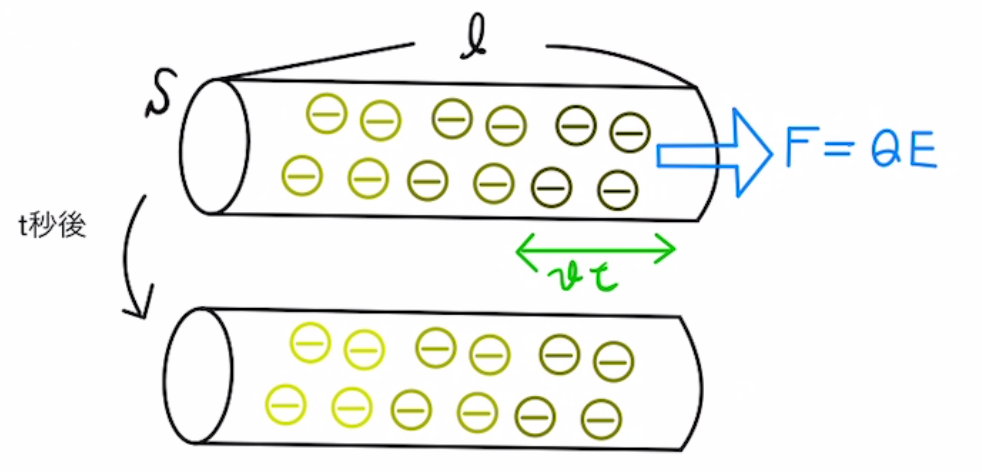
抵抗内のすべての電子にかかる力は
$$F=QE=enSl\frac{V}{l}=enSV$$
となります。
よって$t$秒間に電子がした仕事は
$$W=F・vt=\frac{e^2nS}{kl}V^2t=\frac{V^2}{R}t$$
この電子がした仕事は抵抗にぶつかることによって発熱して外に放出されます。
すなわち、1秒当たりの消費電力は
$$W=\frac{V^2}{R}=RI^2$$
となることがわかります。