(1)
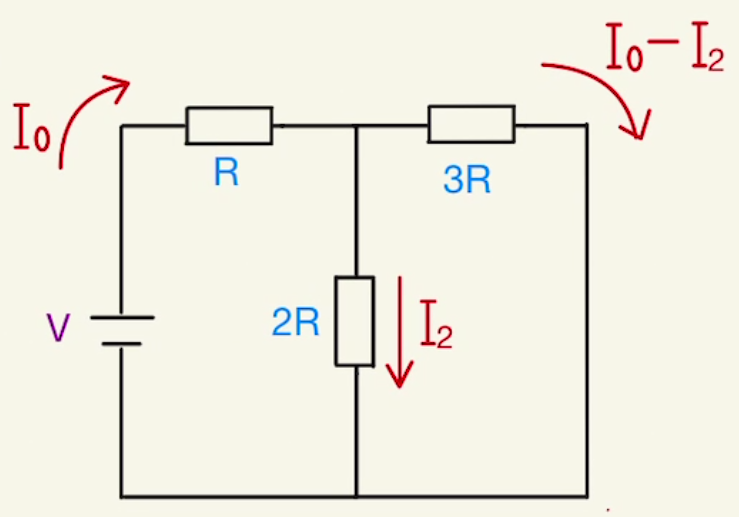
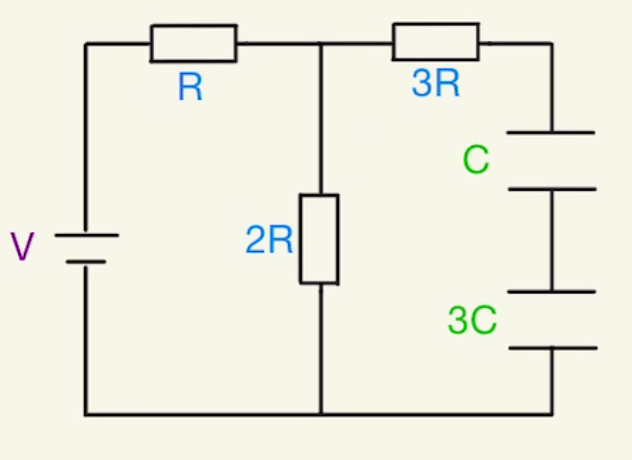
コンデンサーの電荷が0のときは電気をそのまま通します。
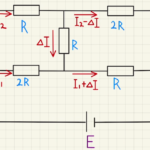
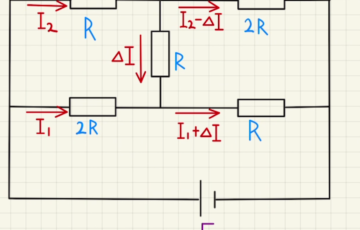
上図のように電流が流れるとすると、それぞれの回路は
$V=RI_0+2RI_2$
$V=RI_0+3R(I_0-I_2)$
となる。この連立式から
$I_0=\frac{5}{11}\frac{V}{R}$
別解

上図のように抵抗だけの回路と考えた時に、抵抗の合成から考えていくこともできます。
$\frac{1}{R_{23}}=\frac{1}{2R}+ \frac{1}{3R}$
より$R_{23}= \frac{6}{5}R$
$R_{123}=R+ R_{23}$
より$R_{123}= \frac{11}{5}R$
よって$I_0= \frac{V}{R_{123}} =\frac{5}{11}\frac{V}{R}$
(2)
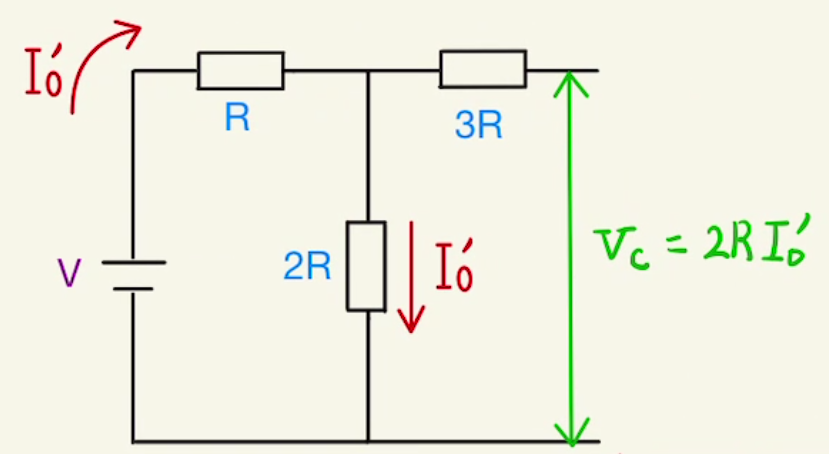
コンデンサーに電荷が十分にたまると、電流が流れなくなります。
そのため、図のような回路と同等になり、
$V=RI’_0+2RI’_0 $
$I’_0=\frac{V}{3R} $
また、コンデンサー間の電位差は$V_c = 2R I’_0 =\frac{2}{3}V$
(3)
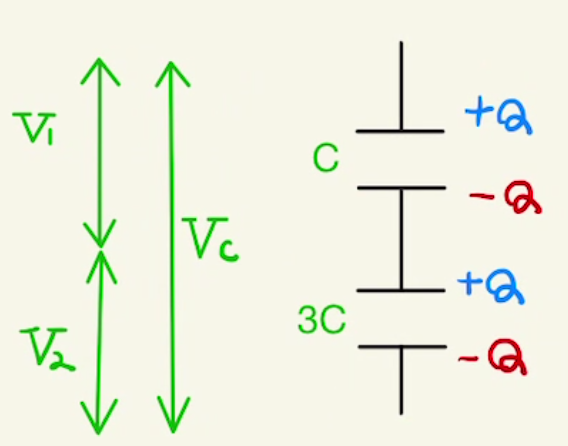
コンデンサーの部分だけ見ていきます。
中央部分は電気的に孤立している、つまり電荷が外に出ていかないので合計は0となります。
そのため、どちらもため込んだ電荷は同じになります。
これを$Q$とすると、コンデンサーの電気容量の式は
$Q=CV_1$
$Q=3CV_2 $
と表されます。
$V_1+V_2=V_c$より、
$Q=\frac{3}{4}CV_c=\frac{1}{2}CV$
(4)
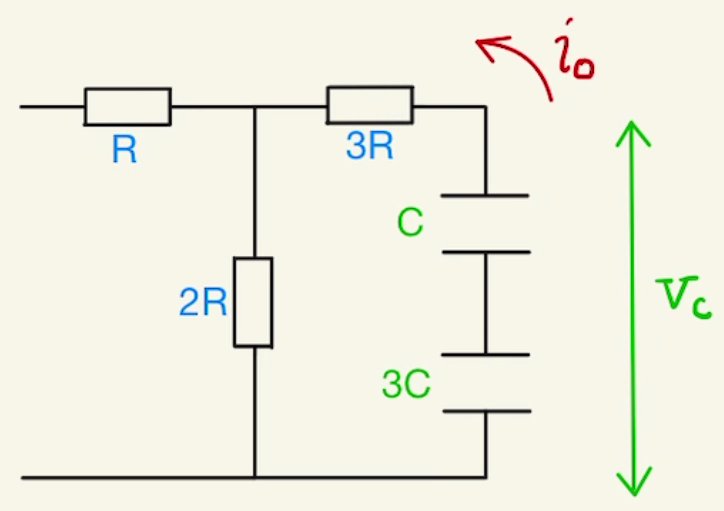
コンデンサーから流れ出した電流を$i_0$とすると、
$V_c=3Ri_0+2Ri_0$
よって$i_0=\frac{1}{5}\frac{V_c}{R}=\frac{2}{15}\frac{V}{R}$
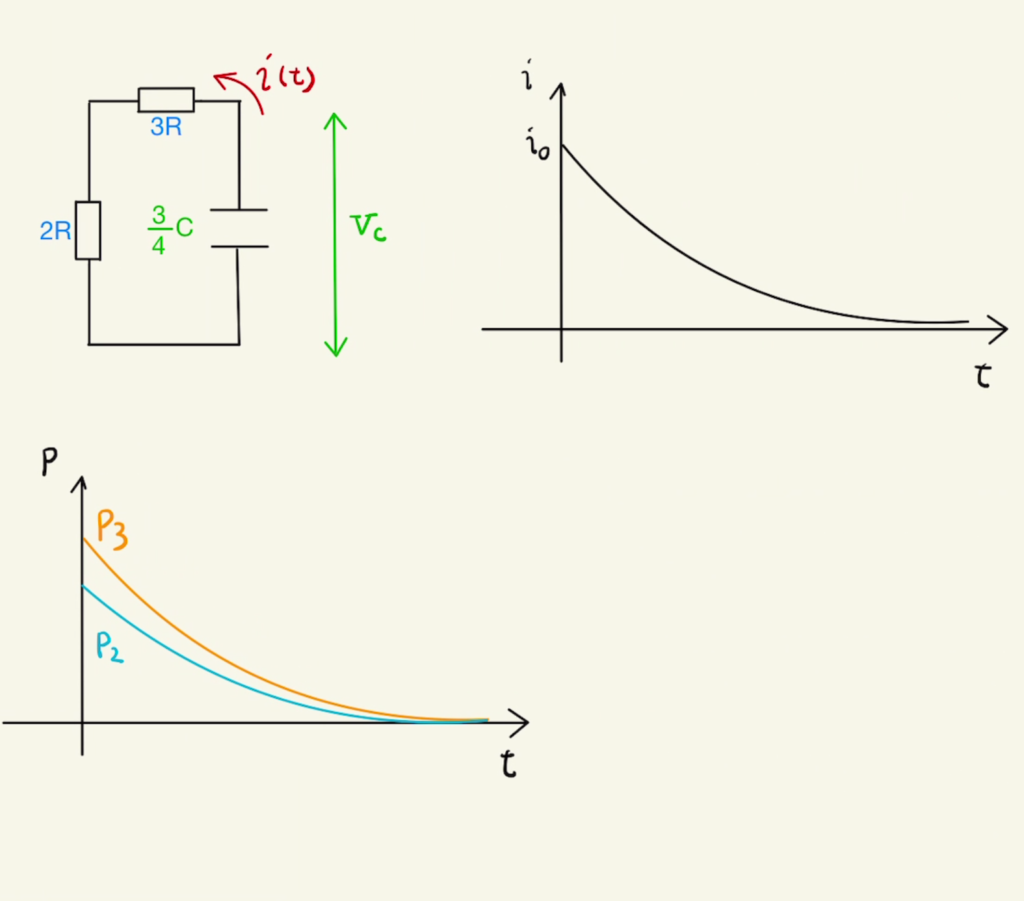
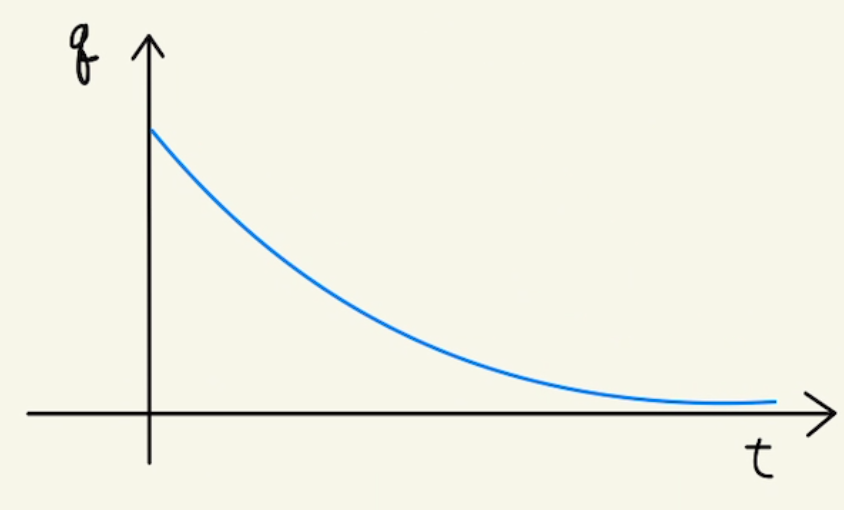
流れる電流は次第に小さくなっていきますが、それぞれの抵抗で時間あたりに消費される電力は常に
$P_2:P_3=2Ri_0^2: 3Ri_0^2=2:3$になります。
そのため、消費電力の合計も図の面積分であるため、
$W_2:W_3= \int_0^∞{P_2dt}: \int_0^∞{P_3dt} =2:3$
となります。
コンデンサーのエネルギーは全て抵抗で消費されるため、
$W_2+W_3=\frac{1}{2} \frac{Q^2}{C} + \frac{Q^2}{3C} $
$W_3 =\frac{3}{5} ( \frac{1}{2} \frac{Q^2}{C} + \frac{1}{2} \frac{Q^2}{3C} )= \frac{1}{10} CV^2$
補足
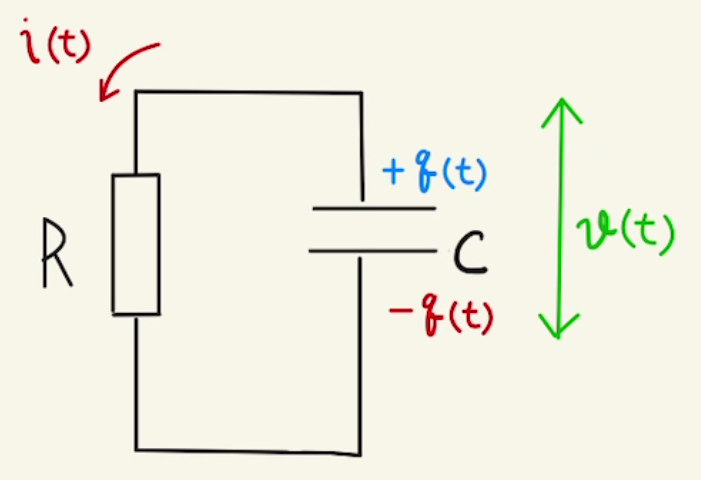
上図のような抵抗とコンデンサーだけの回路の場合、ためられた電気量や電流は指数関数として減少していきます。(一定時間たつと半分、同じ時間たつとさらに半分…といった減少のしかたです。)
詳しくはコンデンサーの電荷の変化をご覧ください。