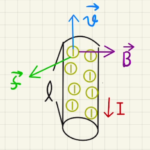
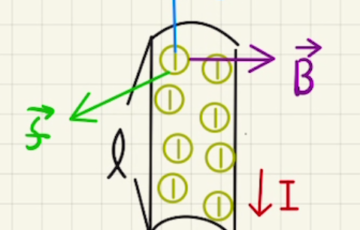
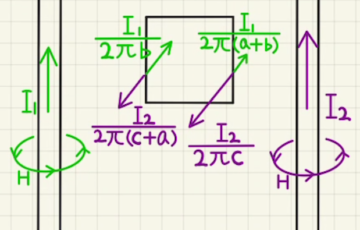
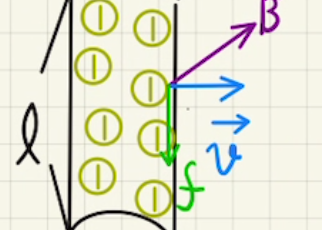
$I_1$は紙面手前に向かって電流が流れ、$I_2$は紙面奥に向かって電流が流れています。
右ネジの方向に従って図のような磁場を発生させます。
$H_0$ではどちらの電流も、$y$の正の方向に$\frac{I}{2πa}$だけ磁場を発生させるため、
$$H_0=2×\frac{I}{2πa}= \frac{I}{πa} $$
$H_1$ではどちらの電流も、図の方向に$\frac{I}{2π(2a)}$だけ磁場を発生させるため、
$$\vec{ H_1 } = \frac{I}{2π(2a)} \begin{bmatrix} -\frac{\sqrt{3}}{2} \\ \frac{1}{2} \end{bmatrix} + \frac{I}{2π(2a)} \begin{bmatrix} \frac{\sqrt{3}}{2} \\ \frac{1}{2} \end{bmatrix} = \frac{I}{4πa} \begin{bmatrix} 0 \\ 1 \end{bmatrix} $$
よって
$$H_1= \frac{I}{4πa} = \frac{1}{4} H_0 $$
$x=b$で発生する磁場は
$$\vec{ H_2 } = \frac{I}{2π(b+a)} \begin{bmatrix} 0 \\ 1 \end{bmatrix} + \frac{I}{2π(b-a)} \begin{bmatrix} 0 \\ -1 \end{bmatrix} = \frac{I}{4πa} \begin{bmatrix} 0 \\ 1 \end{bmatrix} = -\frac{I}{2π} \frac{2a}{ b^2-a^2} \begin{bmatrix} 0 \\ 1 \end{bmatrix} $$
よって磁場の大きさは
$$H_2= \frac{I}{2π} \frac{2a}{ b^2-a^2} = \frac{I}{4πa} \frac{4a^2}{ b^2-a^2}= \frac{4a^2}{ b^2-a^2}H_1 $$
この係数が1となるのは$b^2=5a^2$⇒$b=\sqrt{5}a$(∵$b>0$)