ミリカンの油滴実験
電子(電荷の最小単位)の存在を確認するための実験です。
電子よりも小さい電荷は存在せず、電子の電荷$e$が最小となります。
そのため電荷も電子何個分かで決まり、全ての電荷が$e$を整数倍したものになります。
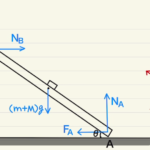
それを利用して以下の実験装置を使いました。
この実験では油滴を上から吹きかけて、油滴の重力と電磁気力の力のつり合いから電荷を調べます。
たくさんの油滴を調べることにより、存在しうる電荷量と存在しえない電荷量が予測できます。
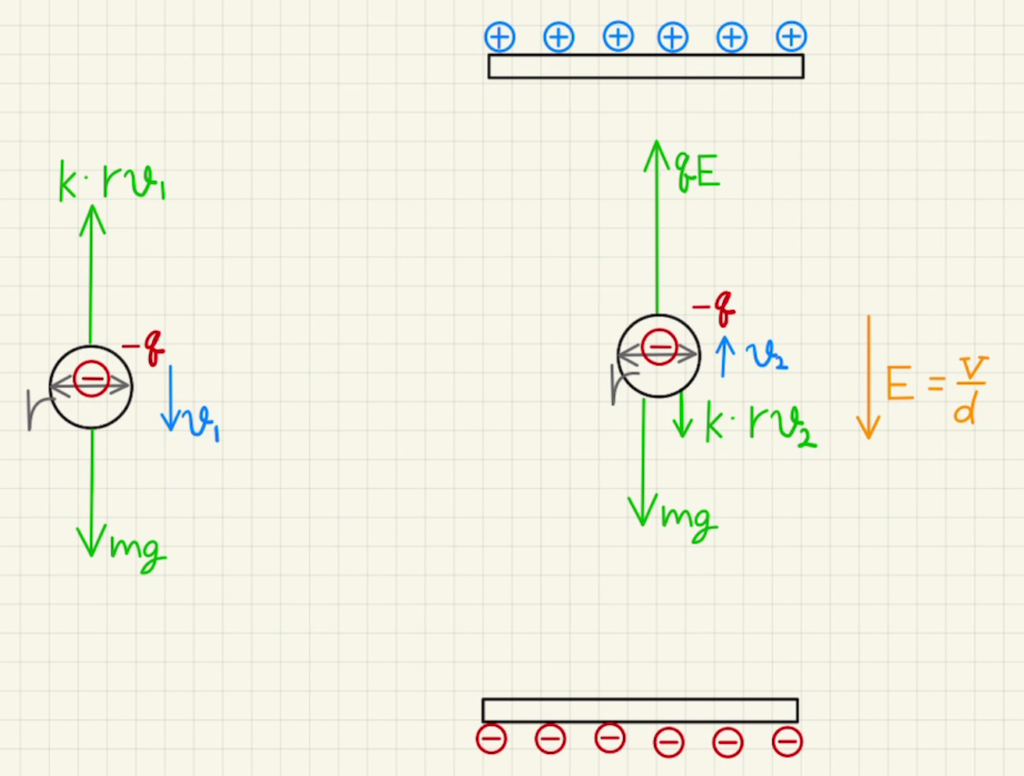
油滴の電荷量を調べるために一定の電圧をかけて力のつり合いを見ます。
油滴にかかる力は三つで、重力、静電気力、空気抵抗となります。
空気抵抗は油滴の半径$r$と速度$v_1$に比例し、定数を$k$とおけば$krv_1$となります。
このことから上に速度$v_1$で上がっているとすると、力のつり合いは
$$0= krv_1+mg-qE ①$$
また、電圧をかけていない状態では下に速度$v_0$で下がっているとすると、力のつり合いは
$$0= -krv_0+mg ②$$
この①-②から
$$q=\frac{k}{E}(v_0+v_1)$$
この方法で多くの油滴の電荷を計測すると、実験では以下のようなプロットができます。
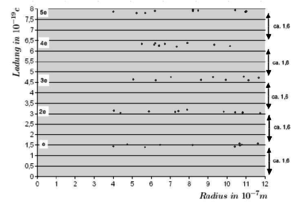
大体$1.5×10^-{-19}[C]$の倍数の周辺にのみ電荷が存在していることがわかります。
このことから、電気量の最小単位は$1.5×10^-{-19}[C]$あたりにあり、これが電子の電気量だと言えます。
全ての電荷はその電子何個分かで表すことができます。
より正確に電子の電荷を調べるためにさらにもう一工夫します。
全ての電子の電気量を平均します。
例を挙げると以下の6個の電荷を観測したとします。(単位:$1.5×10^-{-19}[C]$)
$$1.6, 1.5, 3.1, 3.3, 4.7, 5.0$$
それぞれの電気量は電子の電気量$e$何個分かに換算すると
$$1e, 1e, 2e, 2e, 3e, 3e$$
と考えられるため
$$1.6+1.5+3.1+3.3+4.7+5.0=1e+1e+2e+2e+3e+3e$$
これを計算すると、
$$e=1.60×10^-{-19}$$
とより高精度に電子の電気量を計算することができました。
・補足
油滴は非常に軽いため、すぐに終端速度に達します。
そのため、加速度は$0$となり力のつり合いとしてとらえることができます。
このとき、速度が一定のため速度$v=\frac{L}{t}$($L$:移動距離、$t$:移動時間)として、それぞれ$v_0$,$v_1$を計算しています。
ナビエ–ストークス方程式から$k=6πη$ ($η$:空気の粘性率)と求めることができます。
また、ストークスの式から$r=\sqrt{ \frac{9}{2}\frac{ηv_0}{(ρ-ρ_0)g} }$も求められます。
微分方程式を含む複雑な計算のため、高校範囲で問われることはまずありません。
油滴はほぼ球体ということができるため、密度を$ρ$とすると質量は$m=\frac{4π}{3}r^3ρ$とおけます。
ただし$r^3$を含むと精度に影響が出るため、今回は計算で$mg$を消しています。
また、ミリカンの実験では水を使うと一部蒸発してしまうため、蒸発しにくい油を使用していました。
ホール効果
半導体はn型半導体とp型半導体があります。
・n型半導体
n型はnegative(負価、マイナス)の頭文字のnで、マイナスの電荷である自由電子が動くことで電流となる半導体を表します。
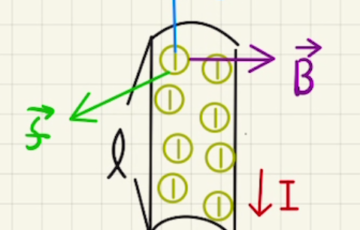
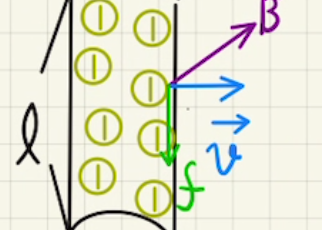
上方向に磁場が発生しているとき、右方向に電流を流した場合を考えます。
このとき、自由電子は左方向に動くため、図のように自由電子は手前方向にローレンツ力がかかります。
すると手前方向は負に帯電し、奥は正に帯電します。コンデンサーのように電荷が分かれるため電場が発生し、自由電子にかかるローレンツ力と電場による静電気力がつり合います。
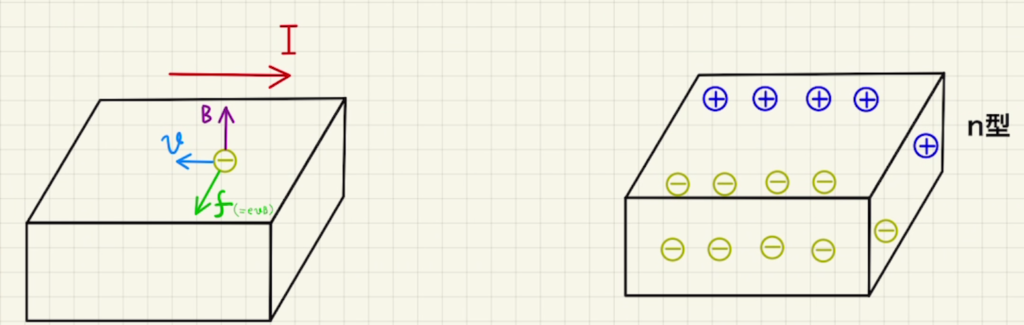
・p型半導体
p型はpositive(正価、プラス)の頭文字のpで、プラスの電荷であるホール(正孔)が動くことで電流となる半導体を表します。
n型のときと同様に上方向に磁場が発生しているとき、右方向に電流を流した場合を考えます。
このとき、正電荷は右方向に動くため、図のように正電荷は手前方向にローレンツ力がかかります。
すると手前方向は正に帯電し、奥は負に帯電します。
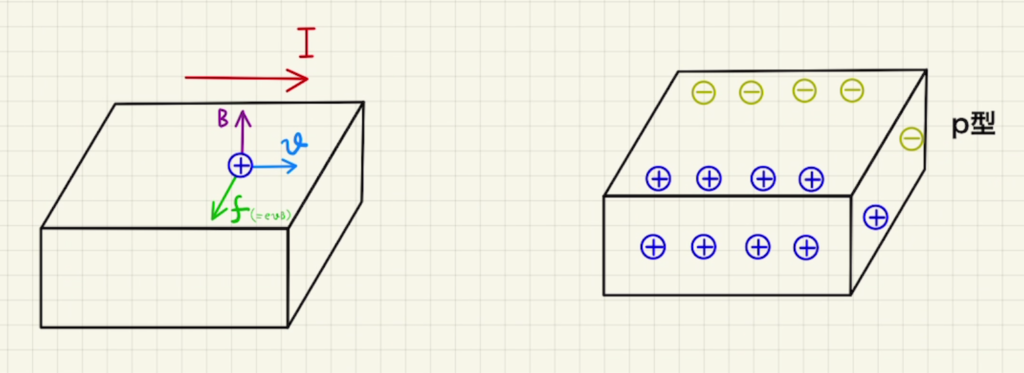
これらの性質は、磁気センサー等に利用されます。
サイクロトロンとベータトロン
電子を回転運動させながら加速し、高速で電子を発射する機器サイクロトロンとベータトロンを紹介します。
これらはガンの治療などに用いられます。