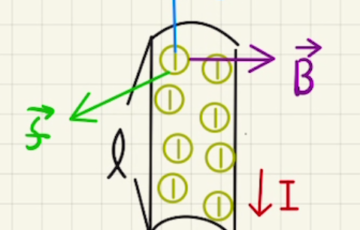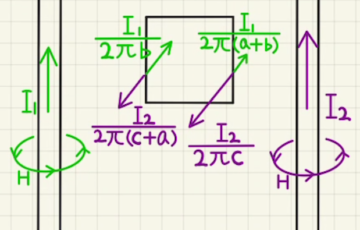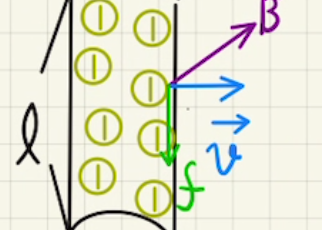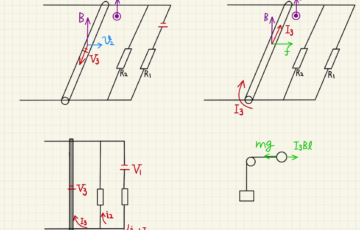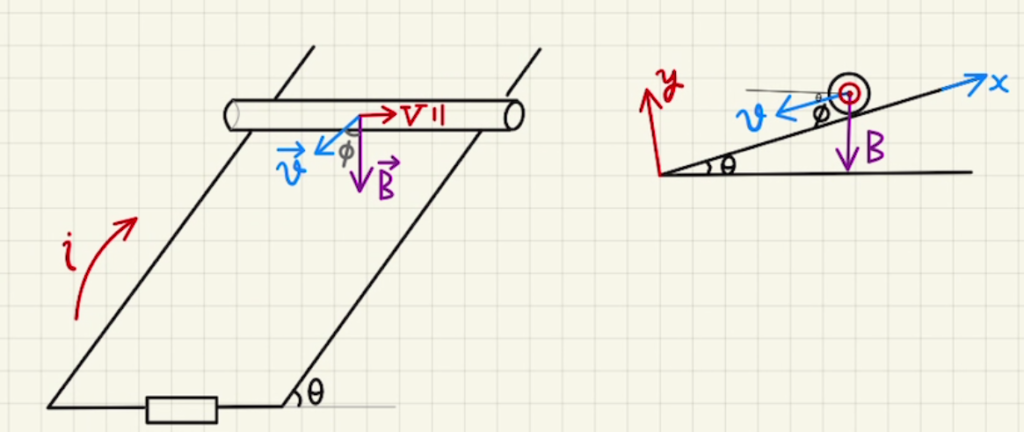
(1)(2)速さ$v$で滑り降りるとき、発生する起電力は
$\vec{V}= \vec{v}× \vec{B}L$
となります。
$\vec{v}$と$\vec{B}$ のなす角度$Φ$は図より$\frac{π}{2}-θ$となるため、
$V=vBL\sin{( \frac{π}{2}-θ )}= vBL\cos{θ} $の大きさの起電力が右方向(b→a)にかかります。
よって流れる電流は
$i=\frac{i}{R}= \frac{ vBL\cos{θ} }{R} $
(3)
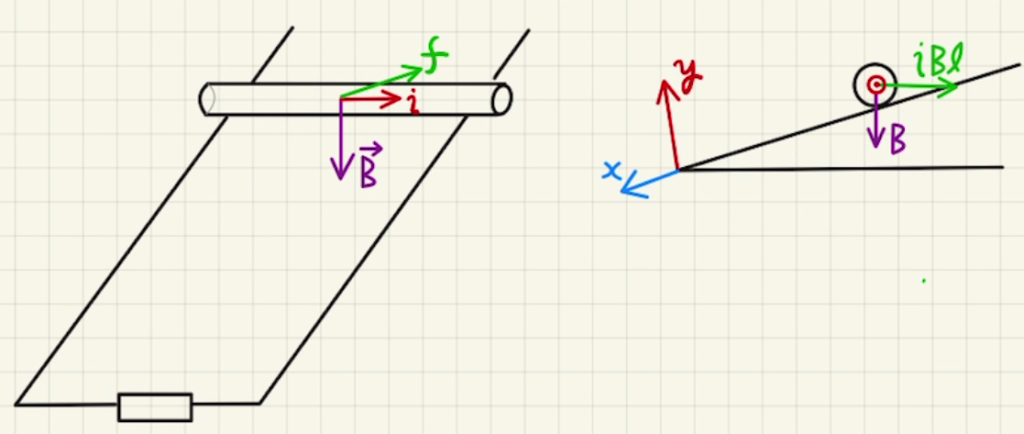
電流$i$が流れるとローレンツ力が発生します。
$\vec{f}=\vec{i}\vec{B}L$
$\vec{i}$と$\vec{B}$は垂直であるため、
$f=iBL$が紙面奥方向にかかります。
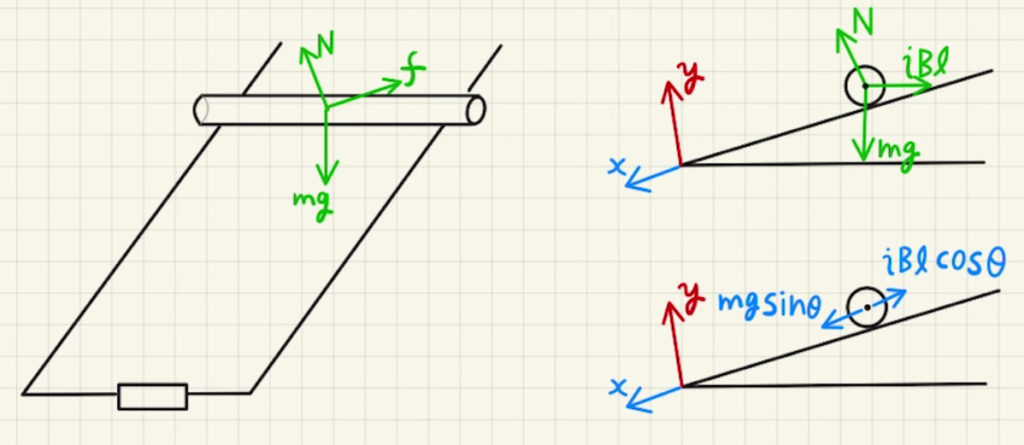
十分時間が経つと、速度が一定となります。
このとき、加速度は$0$なので力は釣り合った状態になります。
$x$方向の力のつり合いは、
$mg\sin{θ}=iBL\cos{θ}$
ここに$i= \frac{ vBL\cos{θ} }{R} $を代入すると
$mg\sin{θ}= \frac{ vBL\cos{θ} }{R} BL\cos{θ}$
$v=\frac{mgR\sin{θ}}{(BL\cos{θ})^2}$
(4)ローレンツ力は仕事をしないため失った重力がそのまま抵抗で消費されるので、直観でも答えが$1$になりそうなのはわかります。
ここでは一応計算をしてみましょう。
$Q=Ri^2 $
また、1秒ごとに$v\sin(θ)$だけ高度が下がるため、
$P=mgv\sin{θ}=mg\frac{Ri}{BL\cos{θ}}\sin{θ} =Ri\frac{ mg\sin{θ} }{ BL\cos{θ} }=Ri^2$
でたしかに$\frac{Q}{P}=1$となることが確認できました。
補足
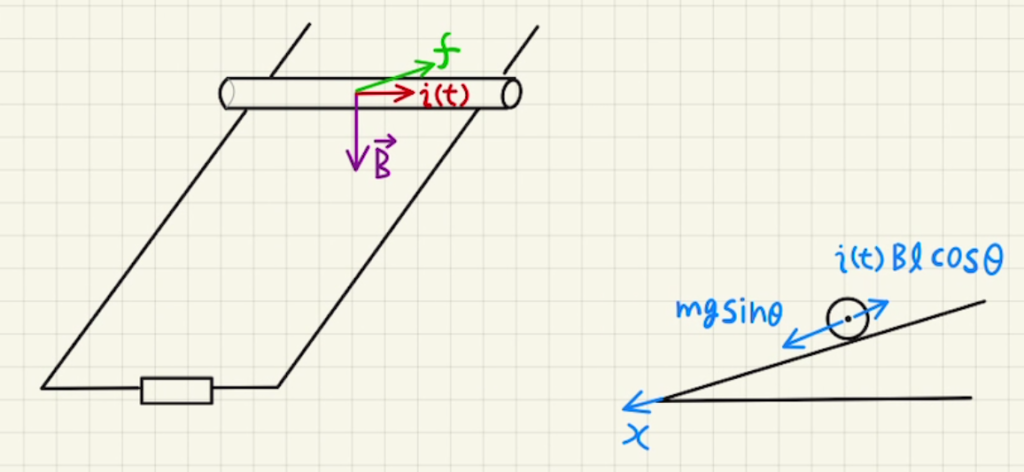
今回の問題では途中経過のことは聞かれませんでしたが、どのように時間変化するのかも見ていきましょう。
とある時刻の図の$x$方向の運動方程式は下のようになります。
$$ma(t)=mg\sin{θ}-i(t)Bl\cos{θ}$$
最初($t=0$)は電流は流れておらず重力だけで転がり落ちていきます。
しかし、速さが大きくなるにつれ大きな電流が流れるようになり、それに従って$x$マイナス方向にも力がかかるようになっていきます。
これが空気抵抗のような働きをします。
$i(t)=\frac{Bl\cos{θ}}{R}v$であることから、
$$ma(t)=mg\sin{θ}- \frac{(Bl\cos{θ})^2}{R} v$$
となります。
$k=\frac{(Bl\cos{θ})^2}{R}$とおけば、
$$ma(t)=mg\sin{θ}- kv$$
となり、空気抵抗の運動方程式と同じになりますね。
以下その証明となります。
式を変形すると、加速度$a$を$\dot{v}$と書き換えて、
$$\dot{v}=-\frac{k}{m}\Bigl( v - \frac{mg\sin{θ}}{k} \Bigr)$$
この微分方程式を解いていくことになります。
$V= v - \frac{mg\sin{θ}}{k} $とおくと、
$$\dot{V}=-\frac{k}{m}V$$
となり、変数分離をすると、
$\frac{dV}{V}=-\frac{k}{m}dt$
これを積分して、
$\log{V(t)}= -\frac{k}{m}t + C_0 $
となります。 $ C_0$は積分定数です。
よって
$$ V(t) = e^{ -\frac{k}{m}t + C_0 } = e^{ C_0 } e^{ -\frac{k}{m}t } $$
となり、
$$ v(t) = e^{ C_0 } e^{ -\frac{k}{m}t }+ \frac{mg\sin{θ}}{k} $$
初速度$v(0)=0$であることから、 $e^{ C_0 } = \frac{mg\sin{θ}}{k} $であることもわかります。
$$ v(t) = \frac{mg\sin{θ}}{k}(1-e^{ -\frac{k}{m}t }) $$
となり、図示すると下の図のようになります。
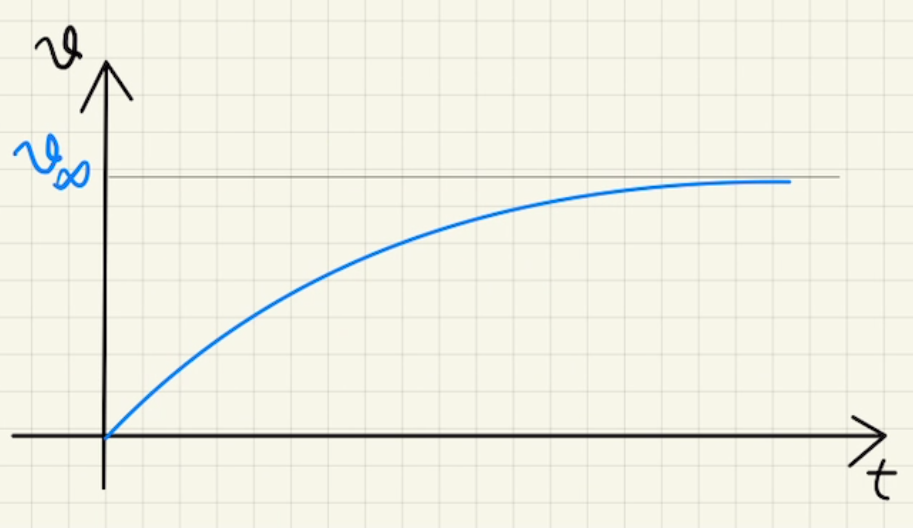
$v_∞= \frac{mg\sin{θ}}{k} =\frac {(Bl\cos{θ})^2}{R} $は終端速度といい、$t→∞$のときに収束していく速さとなります。