電流と磁場は密接な関係にあり、電流(もしくは電荷の移動)は磁場を作り、磁場は起電力を発生させます。
ここではそれぞれの相互的な作用を見ていきます。
ベクトルの外積
方向も含めた電磁場の計算において、ベクトルの外積による表記がよく使われます。
モーメントでも扱いましたが、復習としてもう一度確認しましょう。
ベクトルの外積の定義は以下になります。
$$ \vec{a}×\vec{b} = \begin{bmatrix} a_x \\a_y \\a_z \end{bmatrix}× \begin{bmatrix} b_x \\b_y \\b_z \end{bmatrix} = \begin{bmatrix} a_yb_z-a_zb_y \\ a_zb_x-a_xb_z \\ a_xb_y-a_yb_x \end{bmatrix} $$
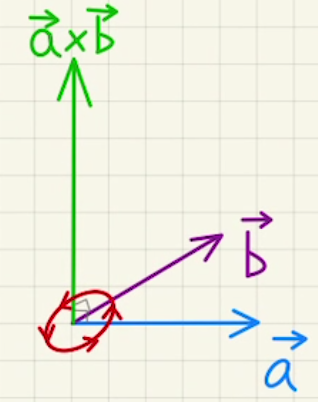
この外積は、$\vec{a}$と $\vec{b}$がつくる平面に対し垂直なベクトルとなります。
向きは $\vec{a}$→$\vec{b}$の順番で右ネジの方向となります。
$ \vec{b}×\vec{a} = -\vec{a}×\vec{b}$となり、順番を間違えると逆向きになってしまうので気を付けてください。
二つのベクトルのなす角を$θ$と置くと、 外積の大きさは
$$|\vec{a}×\vec{b}|=ab\sin{θ}$$
となります。内積の$\cos$の形とは逆ですね。
二つのベクトルが平行であれば $|\vec{a}×\vec{b}|=0$、垂直であれば $|\vec{a}×\vec{b}|=ab$ となります。
電流が作る磁場
電流が流れているときにまわりに磁場が発生します。
ここでは、直線を流れる電流、円を流れる電流、ソレノイド・コイルについて扱います。
正直、公式の丸暗記でかまいません。もし、より原理に近いところからを見たい場合は、ビオ・サバールの法則を参考にしてください。
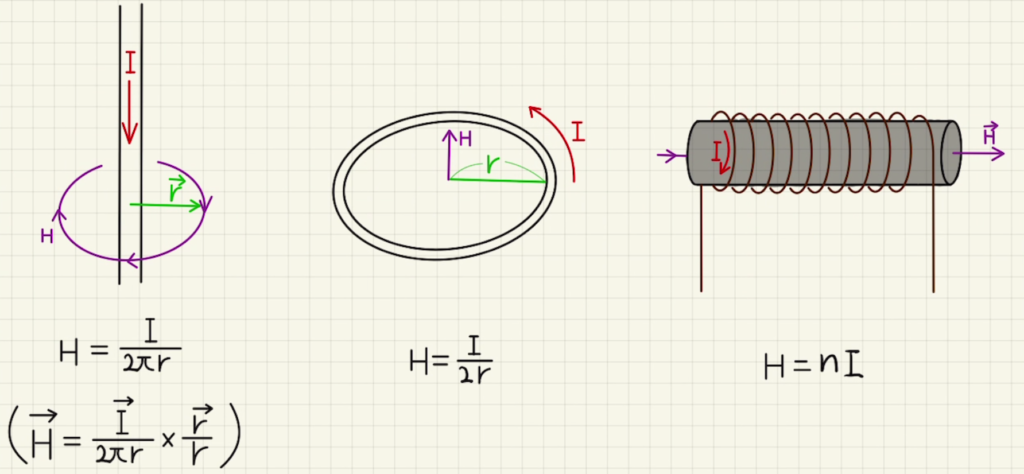
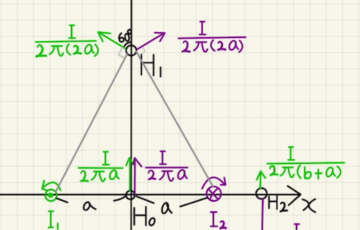
・直線を流れる電流
直線に流れる電流が距離$r$だけ離れた場所に作る磁場 は
$$ H=\frac{I}{2πr}$$
となります。
また、ベクトルで表記すると、
$$ \vec{H}=\frac{\vec{I}}{2πr}×\frac{\vec{r}}{r}$$
・円を流れる電流
円に流れる電流が円中央に作る磁場は
$$ H=\frac{I}{2r}$$
となります。
また、向きは電流の右ネジ方向となります。
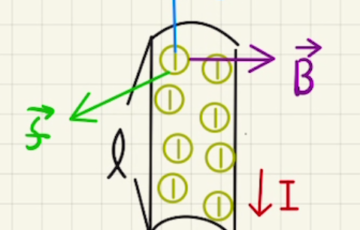
・ソレノイド・コイルに流れる電流
1[m]あたりの巻き数を$n$としたとき、 電流がコイル内部作る磁場は
$$ H=nI$$
となります。
向きは電流の右ネジの方向となります。
コイルの外部には磁場は発生させません。
また、コイルの端の部分は磁場はその半分の$H’=\frac{1}{2}nI$となります。
磁場によるローレンツ力
・磁場と磁束密度
ここからは磁場だけでなく磁束密度というものが出てきます。
$\vec{B}=μ\vec{H}$で表されます。
$\vec{B}$:磁束密度 $μ:$透磁率 $\vec{H}:$磁場
基本的に同じようなものと考えてもらってもよいです。
磁場の発生する物体(水や金属など)によって磁場の影響度合いが強くなることがあります。そのため、その影響割合をかけたものを磁束密度と呼ぶと考えてください。
(電気でいえば、電場→磁場、磁束→電気力線、透磁率→誘電率)
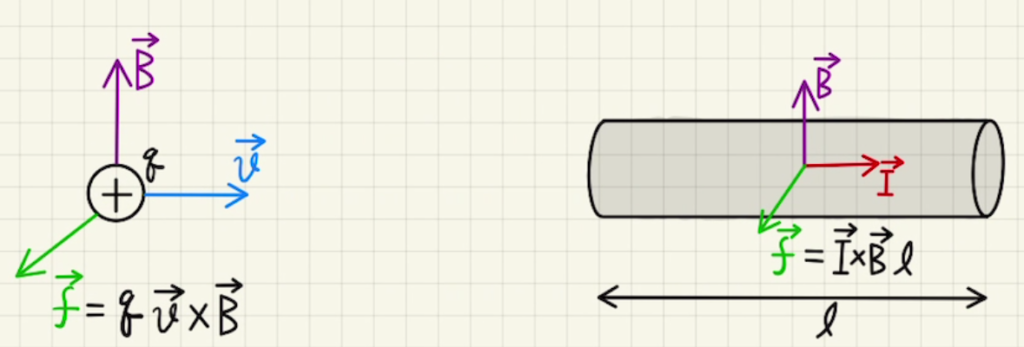
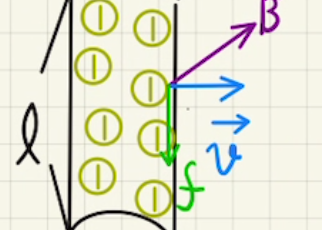
・動く電荷
正の電荷が動くとき、電荷に力が発生します。
その力は以下で表されます。
$$\vec{f}=q\vec{v}×\vec{B}$$
これをローレンツ力と言います。
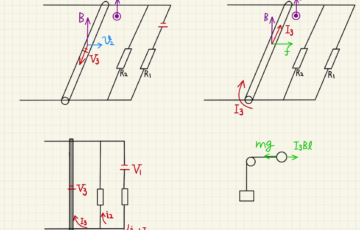
・電流が流れる金属棒
電流は電荷の移動なので、導線に電流が流れるとローレンツ力が発生します。
かかる力は
$$\vec{f}=\vec{I}×\vec{B}l$$
良問の風118などのように動く電荷から求めることもできます。
誘導起電力
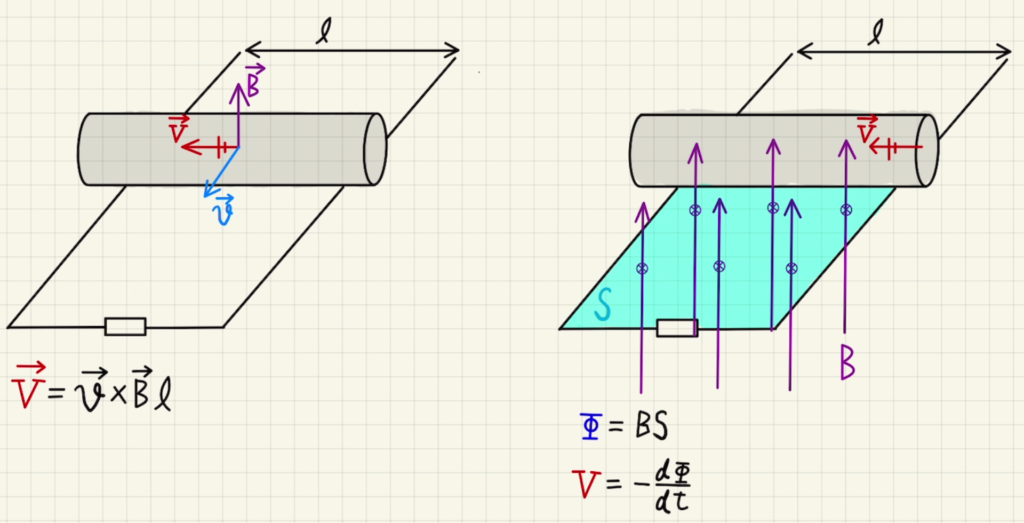
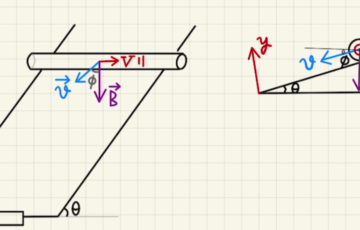
・動く金属棒
磁場の中で金属の棒が動くと起電力が発生します。
レールの幅を$l$とすると発生する起電力は
$$\vec{V}= \vec{v}×\vec{B}l$$
となります。
これを誘導起電力と言います。
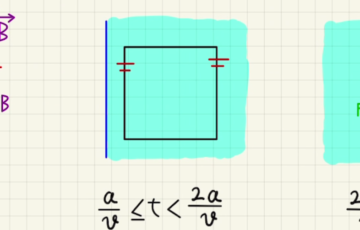
・回路の内側に磁束が発生している場合
上の場合直線状に伸びた金属限定ですが、形状を無視できるより一般化した誘導起電力の説明の仕方もあります。
ある閉回路があり、その内部の磁束が変化するとき、以下のような起電力が発生します。
$$V= -\frac{dΦ}{dt}$$
このマイナスは、誘導起電力によって発生した電流が磁束変化を減らす(変化に抗う)向きに磁場を発生させることになることを示しています。
コイルのインダクタンス
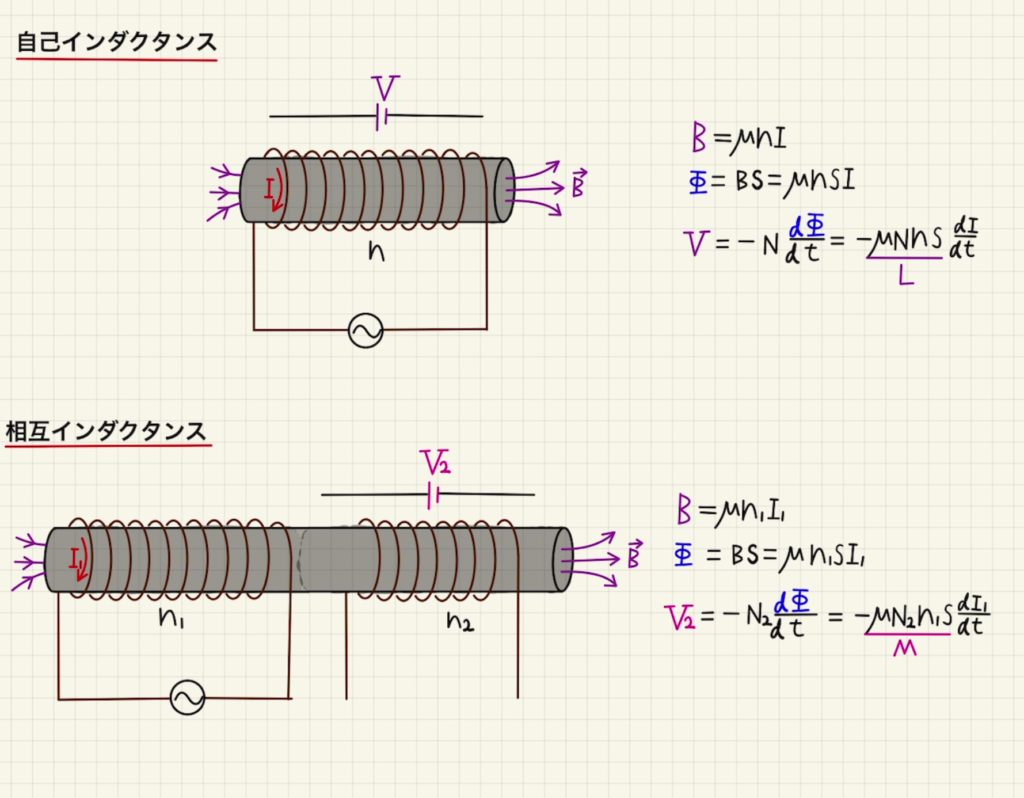
・自己インダクタンス
コイルに流れる電流が大きくなると、逆向きに起電力が発生します。
その原理についてみていきましょう。
コイルに電流が流れると、磁場を発生させます。
そのとき、磁束密度は以下になります。
$B=μnI$ ($n$:1m当たりの巻き数)
これに面積をかけると平面を通る磁束となります。
$Φ=μnSI$
コイルの回路を通る磁束はこれにコイルの総巻き数$N$をかけたもので、$NΦ$です。
よって、コイルに発生する磁場は
$V=-\frac{d{ NΦ }}{dt} = -N\frac{dΦ}{dt}= – μnNS\frac{dI}{dt} $
となります。
この$μnNS=L$を自己インダクタンスと言い、どれだけ強く電流の増加に反発するかを表します。
マイナスは電流が増える方向とは逆向きに電流を流すことを意味します。
流れとしては
電流が増加→磁束が増加→誘導起電力が発生
となりますね。
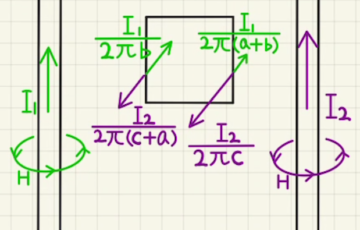
・相互インダクタンス
同じ磁場を共有する二つのコイルがある場合も似たような現象が起きます。
磁場を共有させるには、同じ鉄心に通すか上にかぶせる必要があります。
コイル1に流れる電流が増えると、磁束が増えてコイル2にも誘導起電力が発生します。
平面を通る磁束は以下になります。
$Φ=μn_1SI$ ($n_1$:コイル1の1m当たりの巻き数)
コイル2の回路を通る磁束はこれにコイル2の総巻き数$N_2$をかけたもので、$N_2Φ$です。
よって、コイルに発生する磁場は
$V_2=-\frac{d{ (N_2Φ) }}{dt} = -N_2\frac{dΦ}{dt}= – μn_1N_2S\frac{dI}{dt} $
この$μn_1N_2S=M$を相互インダクタンスと言い、どれだけ強く別のコイルに電圧を発生させるかを表します。
電圧は$N_2$に比例することから、変圧器として使われます。
実際の変圧器では下のような一周させたような金属の両サイドにコイルを巻き、磁束を共有させます。
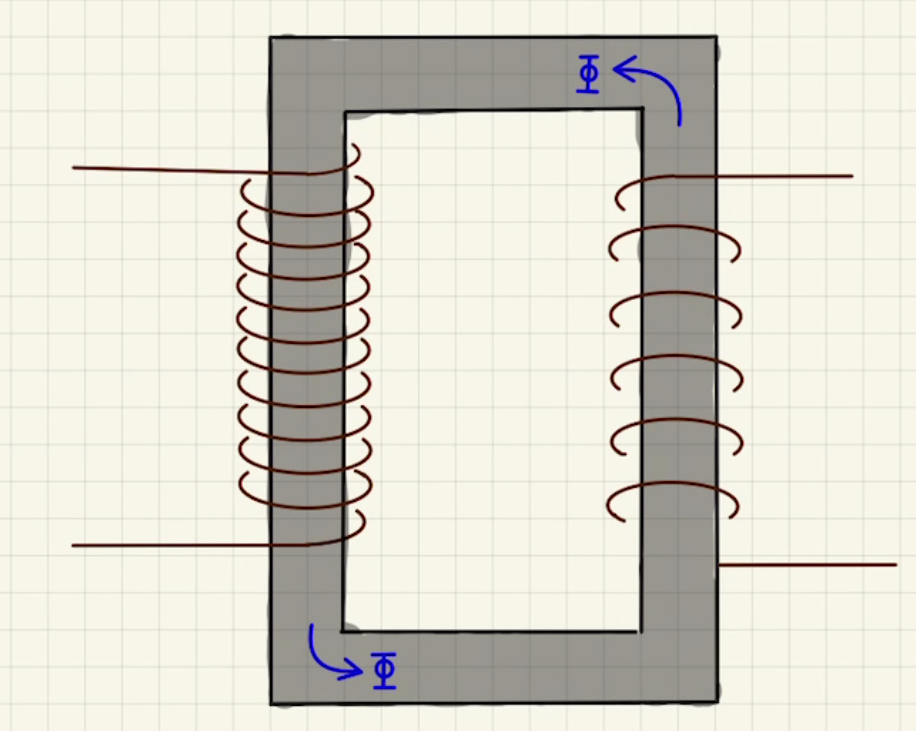
まとめ
・電流が流れると以下の大きさの磁場が発生する
直線: $ H=\frac{I}{2πr}$
円形: $ H=\frac{I}{2r}$
コイル: $ H=nI$
・磁束密度$\vec{B}$は磁場の影響力で、物質により変わり
$\vec{B}=μ\vec{H}$で定義される。
・電荷が動くと以下のローレンツ力が発生する
$\vec{f}=q\vec{v}×\vec{B}$
このことから、長さ$l$の棒に電流$\vec{I}$が流れると以下のローレンツ力が発生する
$\vec{f}=\vec{I}×\vec{B}l$
・長さ$l$の棒が速度$\vec{v}$動くと以下の電圧が発生する
$\vec{V}= \vec{v}×\vec{B}l $
回路の磁束の総量から計算することもでき、
$\vec{V}= -\frac{dΦ}{dt}$
となる。このマイナスは誘導起電力により、磁場の変化を減らす方向に電流が流れることを意味する。
・コイルでは自らが発生させた磁場の影響を受ける
自己インダクタンス:$V=-L\frac{dI}{dt}$
相互インダクタンス:$V_2=-M\frac{dI_1}{dt} $