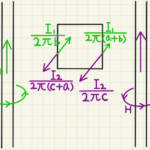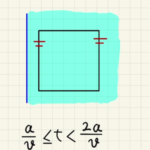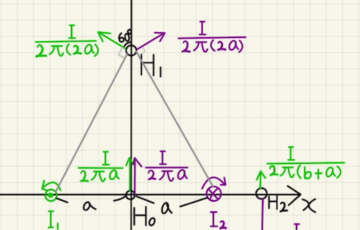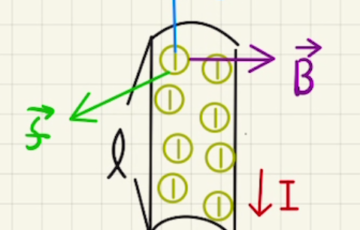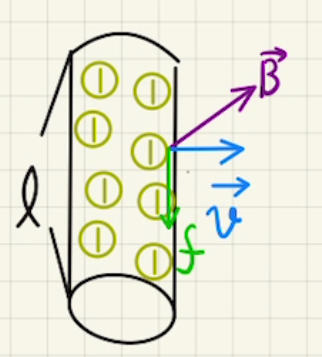
(1)(2)ローレンツ力は
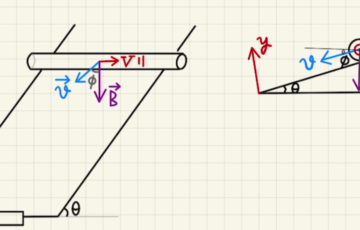
$\vec{f}= -e×\vec{v} \vec{ B }$
となり、 $\vec{v}$と$\vec{B}$は垂直なので、大きさは
$f=evB$で向きは$\vec{v}×\vec{B}$の右ネジ方向の逆となり下方向となります。
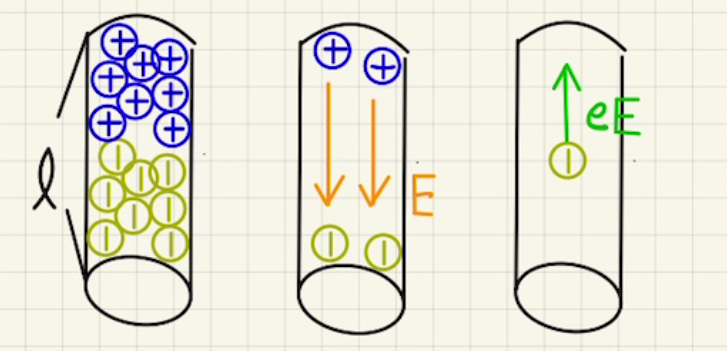
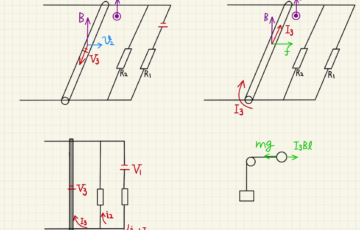
(3)(4)この時、電子は下に引っ張られて下(D)は図のように負に帯電します。
(5)(6)その結果、帯電したコンデンサーのように上から下方面へ電場が発生します。
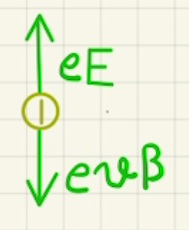
(6)(7)上図のように磁場によってかかる力と電場のよってかかる力釣り合うまで、電子は下に移動し続けます。
丁度つり合いが取れた時、力のつり合いは、
$eE=evB$
となるため、
$E=vB$
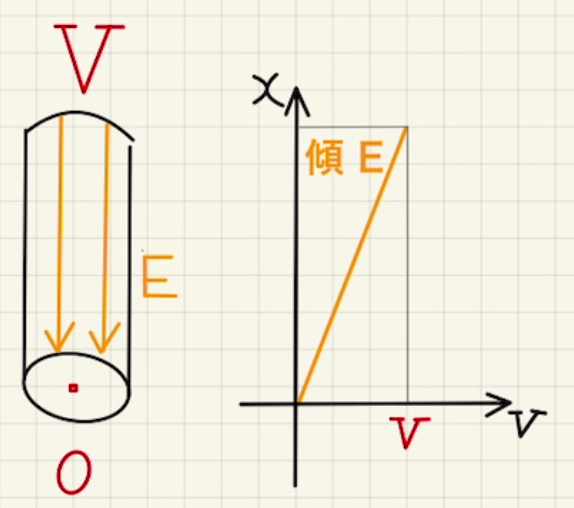
このとき、電場に逆らうように移動すると電位が上がるため、上(C)の方が電位が高くなっています。
電位差は$V=\int_0^l{Edx}=El=vBl$となります。
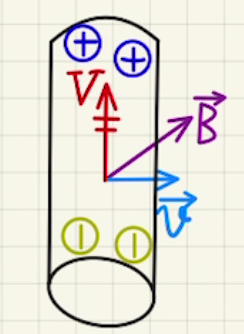
この電位差が起電力になるため、方向も含めた式は
$\vec{V}=\vec{v}×\vec{B}l$の式を導くことができました。