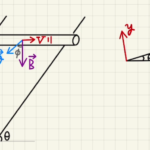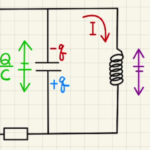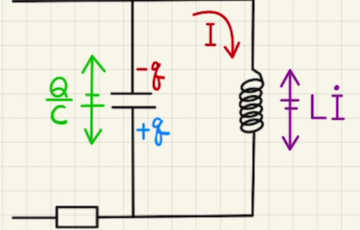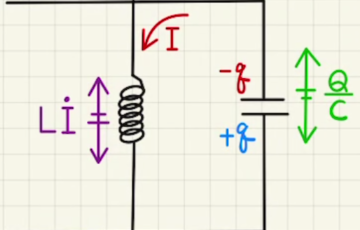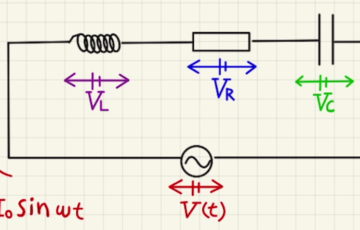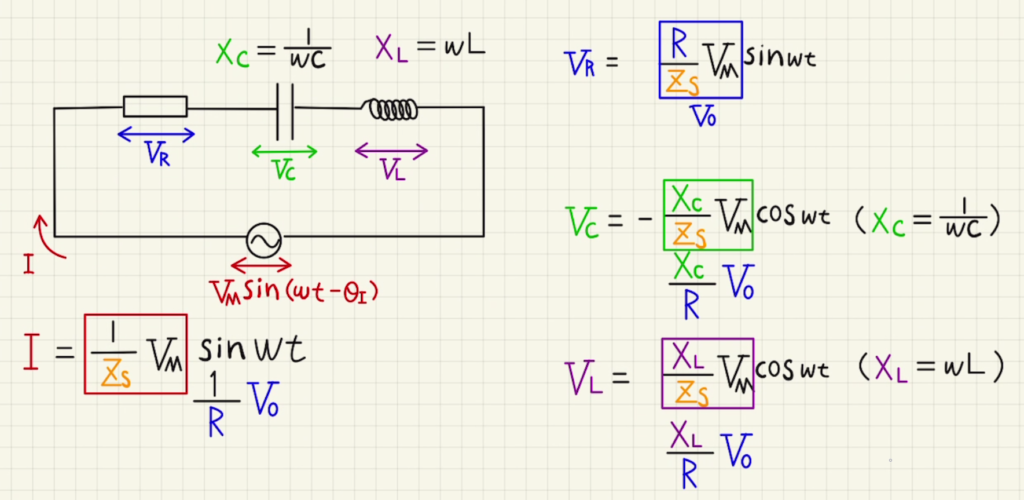
交流のRLC直列回路を参考に式を立てます。
今回の問題では抵抗の間の電位差は$V_0\sin{ωt}$となっています。
電源電圧を$V_M\sin{(ωt-θ_I)} $とすれば、$V_M=\frac{Z_s}{R}V_0$となります。
それぞれのパーツ間の電圧や電流も求められます。
(1) $T=\frac{2π}{ω}$ より、$ω=\frac{2π}{T}$
(2)抵抗間の電圧と電流は一致し、
$$I=\frac{V_0}{R}\sin{ωt}$$
(3)エネルギーは抵抗でのみ消費されます。(熱として外に放出させるため。コンデンサーやコイルはエネルギーを電流によって出し入れしているだけなので、1周期でプラマイゼロになります。)
抵抗間の電圧の実効値を$V_e$とすると、消費電力は
$$\frac{V_e^2}{R}= \frac{V_0^2}{2R} $$
(4)コンデンサー間の電圧は
$$V_C=-\frac{X_C}{R}V_0\cos{ωt}= -\frac{1}{ωCR}V_0\cos{ωt} $$
となります。
そのため、電圧の実効値は $\frac{1}{\sqrt{2}ωCR}V_0 $
(5)電圧$V_C$が0になるのは$\cos{ωt} $が$0$のときで、$ωt=\frac{1}{2}π , \frac{3}{2}π$
よって$t=\frac{T}{4},\frac{3T}{4}$
(6) コイル間の電圧は
$$V_L= \frac{X_L}{R}V_0\cos{ωt}= -\frac{ ωL}{R}V_0\cos{ωt} $$
となります。
そのため、電圧の実効値は $\frac{ωL}{\sqrt{2}R}V_0 $
(7)電源の最大電圧は
$V_1=V_M=\frac{Z_s}{R}V_0= \frac{V_0}{R} \sqrt{ R^2+ ( ωL – \frac{1}{ωC})^2 } $
また、ab間の電圧は
$$V_{ab}=V_R+V_C=V_0\sin{ωt}-\frac{X_C}{R}V_0\cos{ ωt }$$
$$=V_0\sqrt{1+\Bigl(\frac{X_C}{R}\Bigr)^2}\sin{(ωt+θ_{ab})}$$
より、$$V_2= V_0\sqrt{1+\Bigl(\frac{X_C}{R}\Bigr)^2} = V_0\sqrt{1+\Bigl(\frac{1}{ωCR}\Bigr)^2} $$