(1)
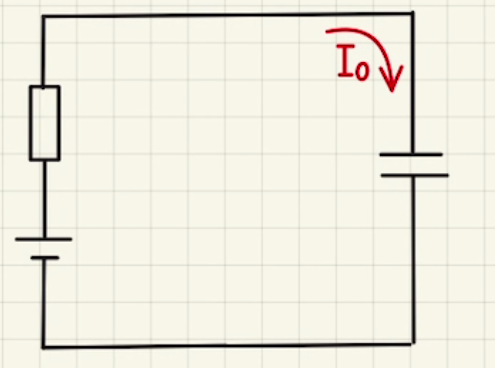
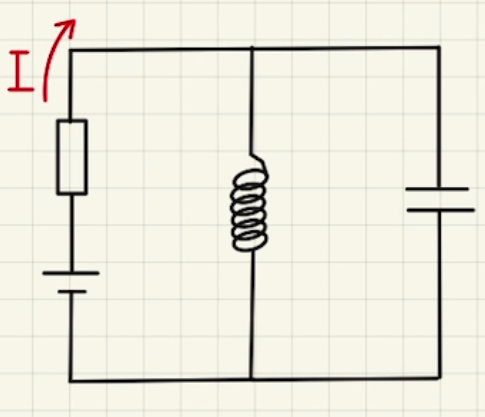
スイッチを入れた瞬間にコイルに急に電流がながれることはないため、コンデンサーのみに電流が流れます。
コンデンサーには電荷がたまっていないため、電位差は$0$で導線と同じように電流が流れます。
よって
$I_0=\frac{V}{R}$
(2)
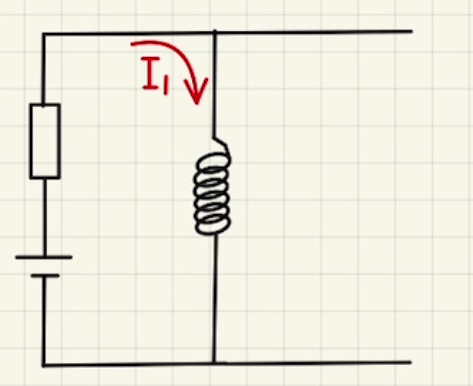
十分に時間が経つと、電流は安定していると考えます。(つまり、$\frac{dI}{dt}=0$)
そのため、コイル間の電圧差は$0$となり、 導線と同じように電流が流れます。
よって
$I_1=\frac{V}{R}$
コンデンサー間の電圧差も$0$であることから、
$Q=CV=0$
補足
LC並列回路は電流が安定するまではとても複雑な動きをします。
高校範囲で扱うことはまずありませんが、興味のある方はこちらを参考にしてください。
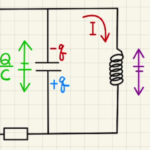
(3)(4)ではLC回路の電気振動になります。
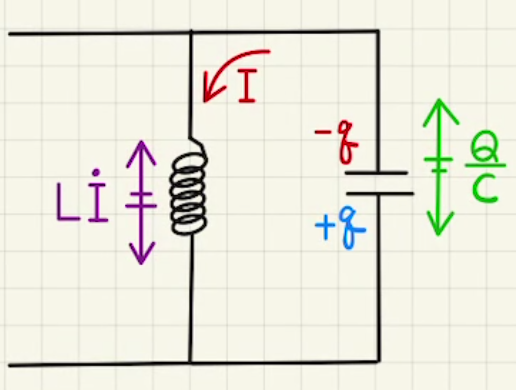
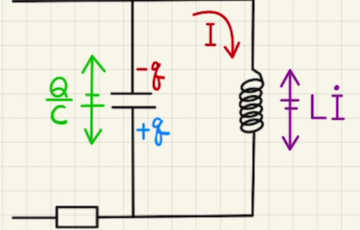
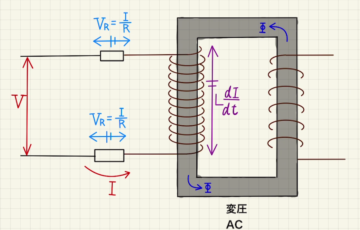
図の回路の方程式は
$\frac{Q}{C}+L\dot{I}=0$
となるため、
$\ddot{I}=-\frac{1}{CL}I$
となります。各振動数$ω= \frac{1}{\sqrt{CL}}$とおいて単振動の微分方程式として解くことができます。
LC回路を参考にすると、流れる電流の推移は、
$I(t) = I(0) \cos{ωt} – Q(0)ω \sin{ωt} $
となり、コンデンサーにたくわえられた電荷は
$Q(t) = \frac{I(0)}{ω} \sin{ωt} + Q(0) \cos{ωt} $
となります。
今回、$t=0$で流れている電流$I(0)$は$I_1=\frac{V}{R}$です。
また、たまっている電荷$Q(0)$は$0$となるため、
となり、コンデンサーにたくわえられた電荷は
$$I(t) = \frac{V}{R} \cos{ωt} $$
$$Q(t) = \frac{V}{Rω} \sin{ωt}$$
(3)最初に$I(t)=0$となるのは$ωt=\frac{π}{2}$
$t=\frac{π}{2ω}= \frac{π}{2} \sqrt{CL} $
(4)コンデンサー間の電圧差は
$V_C=\frac{Q(t)}{C}= \frac{V}{CRω} \sin{ωt} $
よってこの最大値は
$V_M=\frac{V}{CRω}= \frac{V}{R}\sqrt{\frac{L}{C}} $