(1)
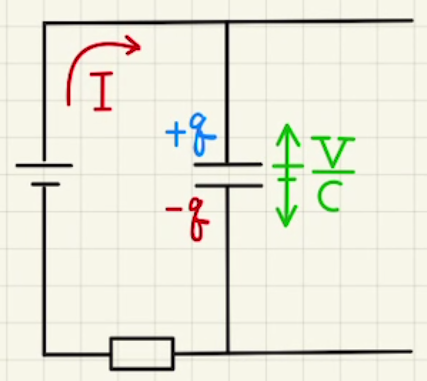
(ア)コンデンサーに電荷がたまっていないときは電位差はなく、そのままそのまま電流が流れます。
そのため、流れる電流は
$I_0=\frac{V}{R}$
(イ)コンデンサーに電荷$q$だけたまっているときは、コンデンサー間の電位差は
$V=\frac{q}{c}+RI$
(ウ)電流が流れなくなると、コンデンサー間の電位差が$V$となるため
$Q=CV$
補足
途中経過の電流をみていきます。
$V=\frac{q}{c}+RI$ より、
$I=\frac{V}{R}-\frac{q}{CR}$
この両辺を時間微分すると、$\frac{dq}{dt}=I$から
$\frac{dI}{dt}=-\frac{I}{CR}$
これは電流が大きいほど、より電流が大きく減少していくことを示しています。
実際にこの微分方程式を変数分離で解き、初期値から積分定数を求めると
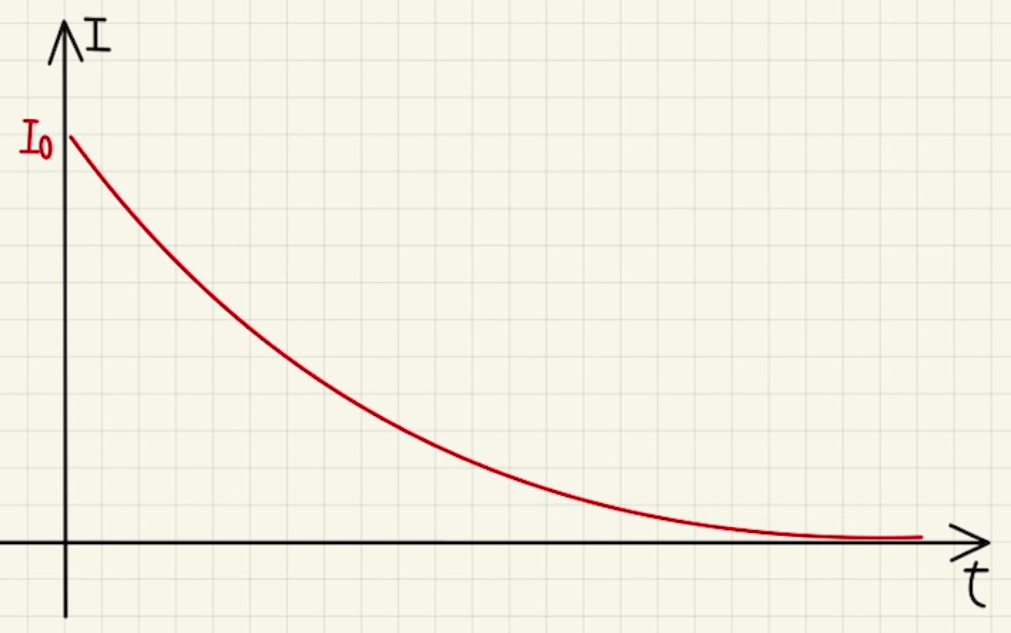
$I=I_0e^{-\frac{1}{RC}t}$
となり、$t→0$で電流が$0$に近づいていくことが確認できます。
計算の詳細はこちらになります。
(2)
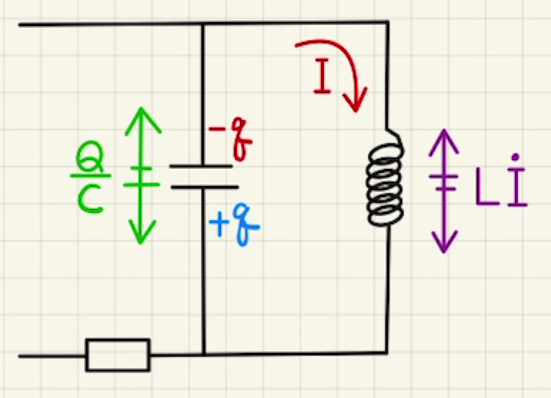
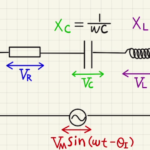
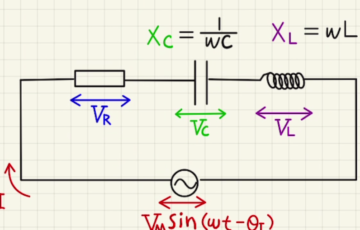
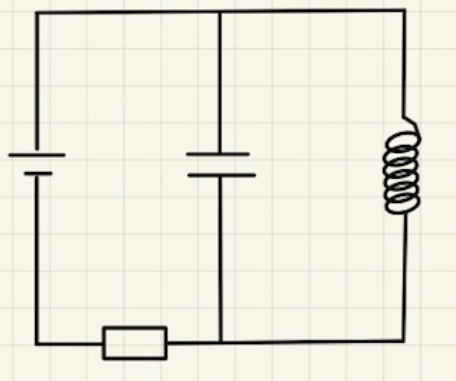
図のような回路の設定にします。
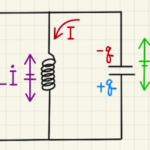
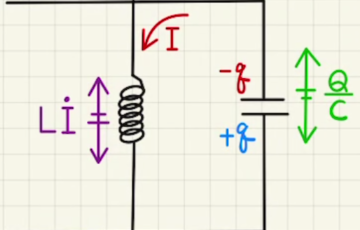
左回りの電流を正とすると、そこから入り込む電流がコンデンサーの電荷となりえます。
その電荷が入り込む側は下なので、今回は下部に電荷がたまっているときを正としましょう。
そのため、最初にたくわえられている電荷は$-CV$となるので注意してください。
回路の方程式は
$\frac{Q}{C}+L\dot{I}=0$
となるため、
$\ddot{I}=-\frac{1}{CL}I$
となります。各振動数$ω= \frac{1}{\sqrt{CL}}$とおいて単振動の微分方程式として解くことができます。
交流のLC回路を参考にすると、流れる電流の推移は、
$I(t) = I(0) \cos{ωt} – Q(0)ω \sin{ωt} $
となり、コンデンサーにたくわえられた電荷は
$Q(t) = \frac{I(0)}{ω} \sin{ωt} + Q(0) \cos{ωt} $
となります。
$I(0)=0, Q(0)=-CV$より
$$I(t) = \frac{V}{Lω} \sin{ωt} $$
$$Q(t) = -CV \cos{ωt} $$
ここまで求まればあとは簡単ですね。
(ア)電流の最大値は$\sin{ωt}=1$のときで、
$\frac{V}{Lω}=V\sqrt{\frac{C}{L}}$
(イ)周期$T=\frac{2π}{ω}= 2π\sqrt{LC}$として
$I(t) = \frac{V}{Lω} \sin{ωt}$を図示すると
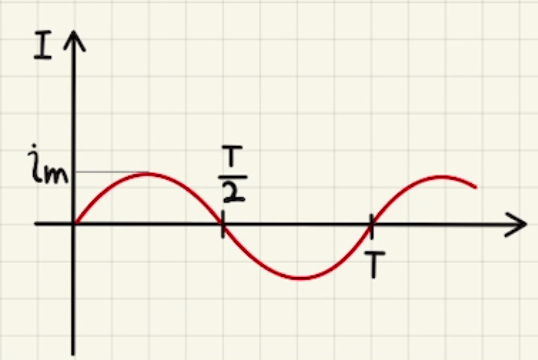
(ウ)最初に電荷が最大になるのは$\cos{ωt}=-1$のとき、$ωt=π$
よって、$t=\frac{π}{ω}=π\sqrt{LC}$