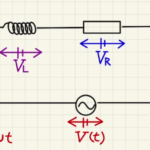
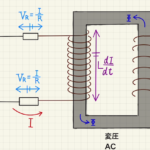
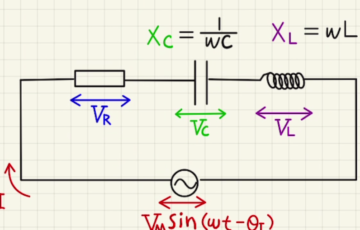
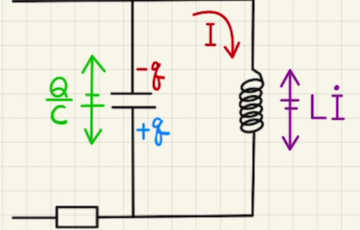
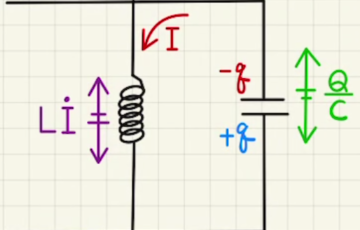
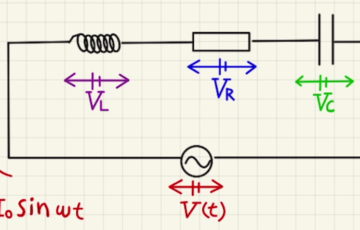
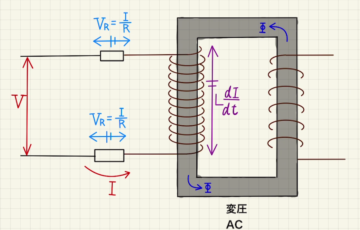
(1) こちらのRLC直列回路を参考に進めていきます。
今回の場合はコンデンサーだけないので$X_C=0$としてインピーダンスが求まります。
ここからオシロスコープにかかる電圧の話になります。
問題文に書いてある通り、飛ばされた電子の位置は電圧に比例すると考えてよく、その係数を$k$とすると
$x=kV$と書くことができます。
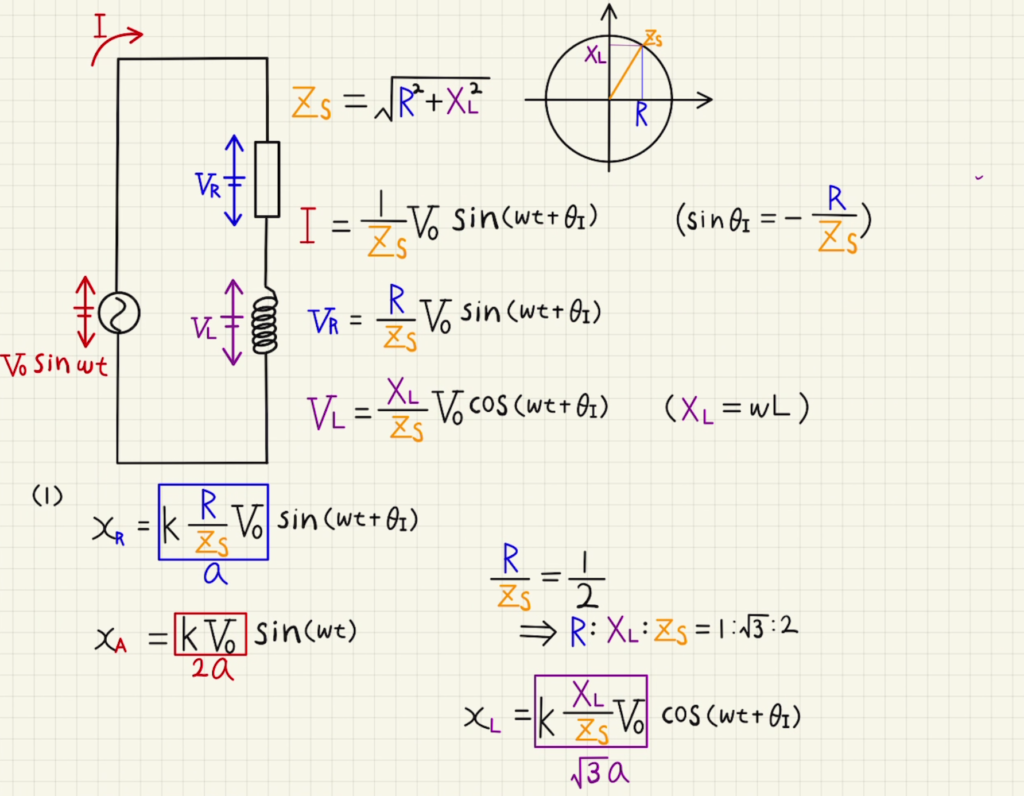
抵抗間で電圧をとると、$x$の位置は
$x_R=kV_R=k\frac{R}{Z_s}V_0\sin{(ωt+θ_I)}$となります。
これが範囲$-a≦x_R≦a$だということなので$\sin$につく係数$ k\frac{R}{Z_s}V_0 $が$a$だということがわかります。
同様に交流電源でも電圧をとると、 $x$の位置は
$x_A=kV=kV_0\sin{(ωt)}$となります。
これが範囲$-2a≦x_R≦2a$だということなので$\sin$につく係数$ kV_0 $が$2a$だということがわかります。
以上のことから$ R:Z_s=1:2$でありインピーダンスの式$Z_s=\sqrt{R^2+X_L^2}$から、 $ R:X_L:Z_s=1:\sqrt{3}:2$とわかります。
コイル間の電圧を取ったとき、 $x$の位置は
$x_L=kV_R=k\frac{X_L}{Z_s}V_0\cos{(ωt+θ_I)}$となります。
この$\cos$の係数は$k\frac{X_L}{Z_s}V_0=\sqrt{3}a$であることがわかりました。
以上のことから、
$-\sqrt{3} a≦x_L≦ \sqrt{3} a$
(2)
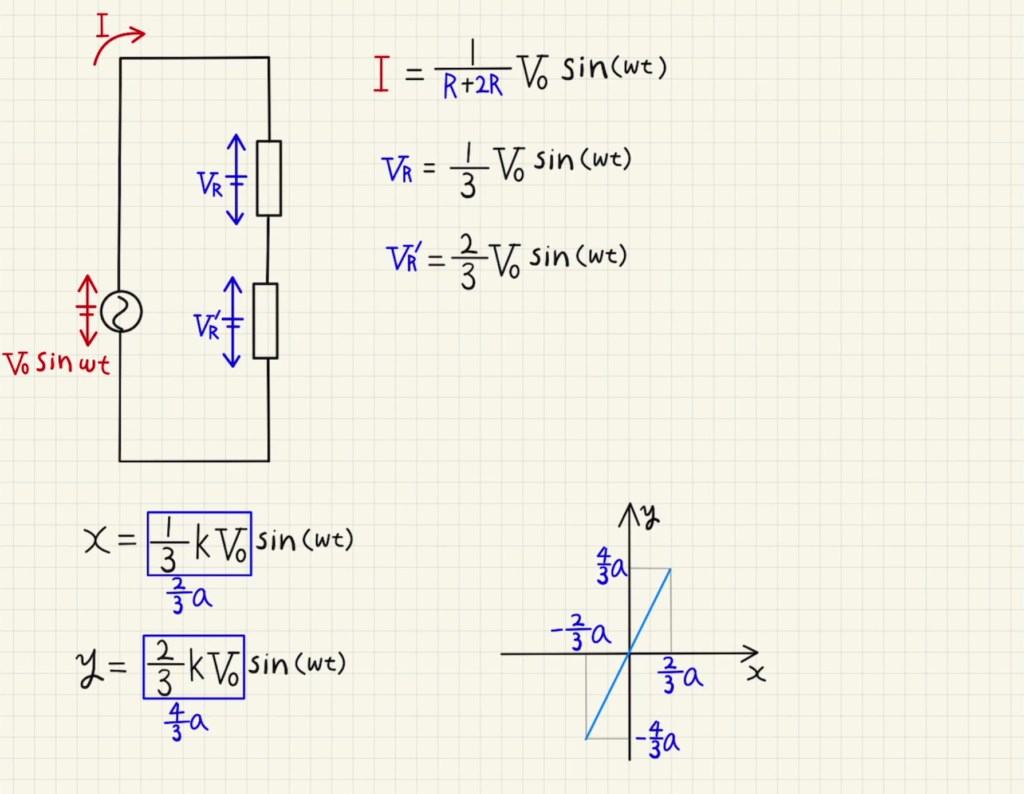
全て抵抗である場合は電流も抵抗間も電源と同じ位相になるため、
$I=\frac{V}{3R}$
$x=RI=\frac{1}{3}kV_0\sin{ωt}=\frac{2}{3}a\sin{ωt} $
$y=2RI=\frac{2}{3}kV_0\sin{ωt}=\frac{4}{3}a\sin{ωt} $
よってこの媒介変数によって表される図は
$y=2x( -\frac{2}{3}a ≦x_L≦ \frac{2}{3}a )$となります。
(3)
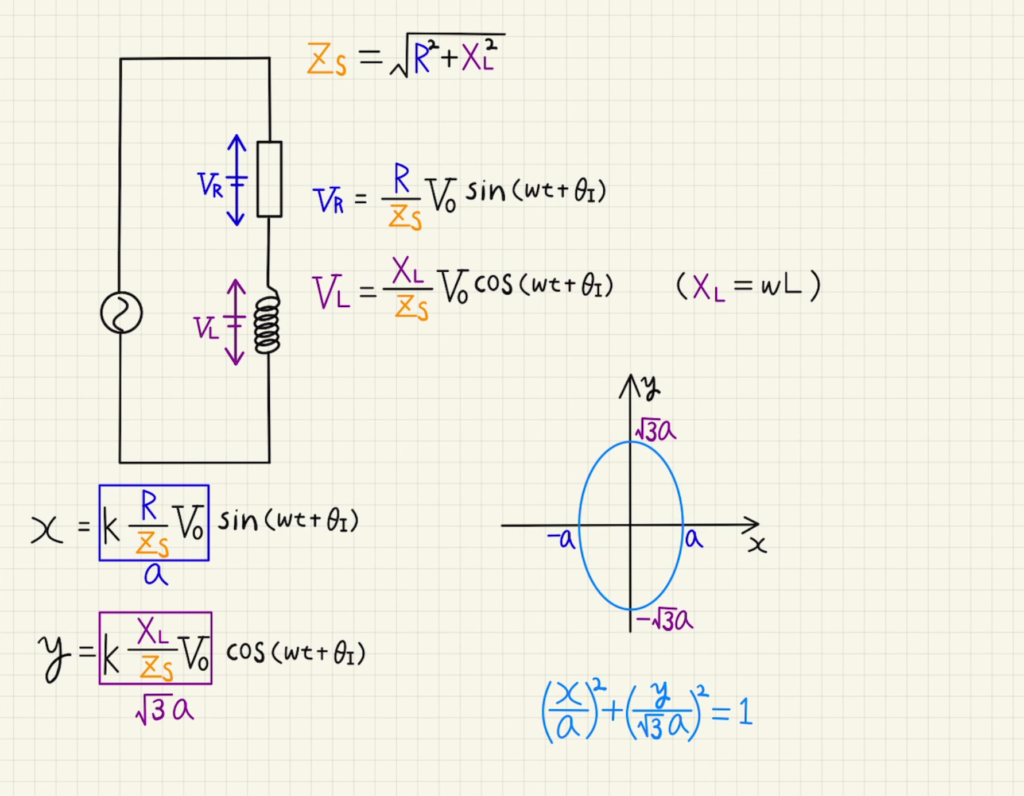
$x$は抵抗間での電圧に比例し、 $y$は抵抗間での電圧に比例し、(1)で求めたように$ R:X_L:Z_s=1:\sqrt{3}:2$及び$kV_0=2a$なので
$x=k\frac{R}{Z_s}V_0\sin{(ωt+θ_I)} = a\sin{(ωt+θ_I)}$
$y=k\frac{X_L}{Z_s}V_0\cos{(ωt+θ_I)} = \sqrt{3}a\cos{(ωt+θ_I)}$
この媒介変数を図示すればよく、
$$\left(\frac{x}{a}\right)^2+\left(\frac{y}{\sqrt{3}a}\right)^2=1$$
楕円形になることがわかります。
(4)

周期を変化させたときの誘導性リアクタンスを$X_L’$とすると、
$x$と$y$の最大値が同じになるとき、円形になるため、
$X_L’=R$となるようにしなければいけません。
$X_L=\sqrt{3}R$であることから、$ω$を$\frac{1}{\sqrt{3}}$にすればよいとわかります。
このとき、 $ R:X’_L:Z’_s= \frac{1}{\sqrt{2}}:\frac{1}{\sqrt{2}}:1$ より、$ \frac{R}{Z_s’}= \frac{1}{\sqrt{2}}$と$ kV_0=2a$ を代入して、
$x=k\frac{R}{Z_s’}V_0\sin{(ωt+θ_I)} = \sqrt{2}a\sin{(ωt+θ_I)}$
$y=k\frac{X_L’}{Z_s’}V_0\cos{(ωt+θ_I)} = \sqrt{2}a\cos{(ωt+θ_I)}$
となることから
$x^2+y^2=2$となるため、半径は$\sqrt{2}$となります。
Q:
交流が$V’=V_0’\sin{(ωt)}$で流れているとすると、
$x=nt (0≦y≦t)$
$y=kV’ = kV_0’\sin{(ωt)}$
この媒介変数を図示すると、 $y= kV_0’\sin{(ω\frac{x}{n})}$となり、
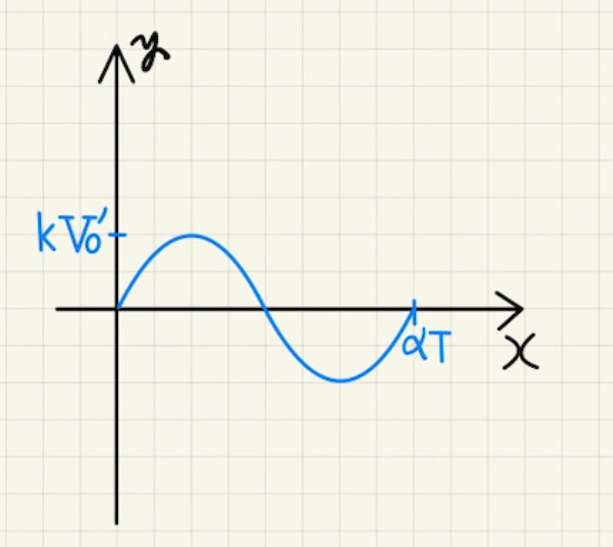
(厳密には、位相を合わせるとは言っていないので位相がずれて$kV_0’\sin{(ω\frac{x}{n})+θ_0)}$のようになり、左に少しズレた形になる可能性はあります。)
補足
今回は断りなしにスクリーンへの衝突位置が電圧に比例すると書かれていますが、その原理について少し考えてみます。
電子が初速度$v_0$で発射されると、板間では電場$E=\frac{V}{d}$が発生し$y$方向に加速します。
通り過ぎた後は等速運動をします。
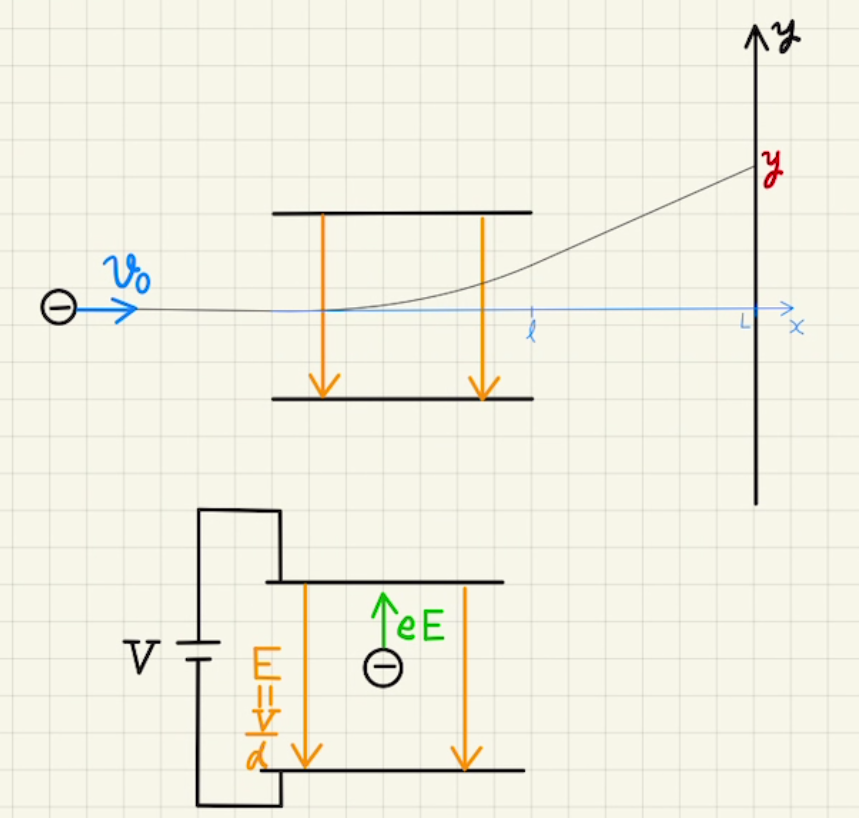
$x$方向は常に速度一定であるため、v-tグラフは下のようになります。
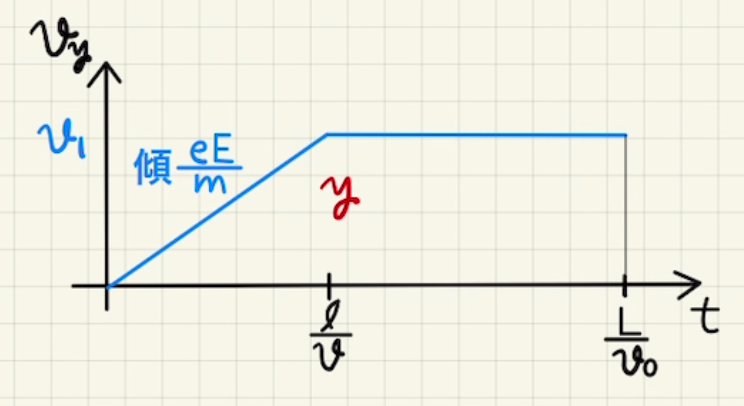
加速後の速度は
$v_1=\frac{eV}{md} \frac{l}{v_0} $
よって、スクリーンへの衝突位置は
$y= \frac{L}{v_0}v_1-\frac{1}{2} \frac{l}{v_0}v_1= \frac{el(2L-l)}{2mdv_0^2}V $
となり、電圧に比例することが確認できます。