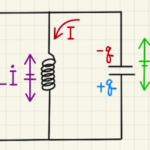
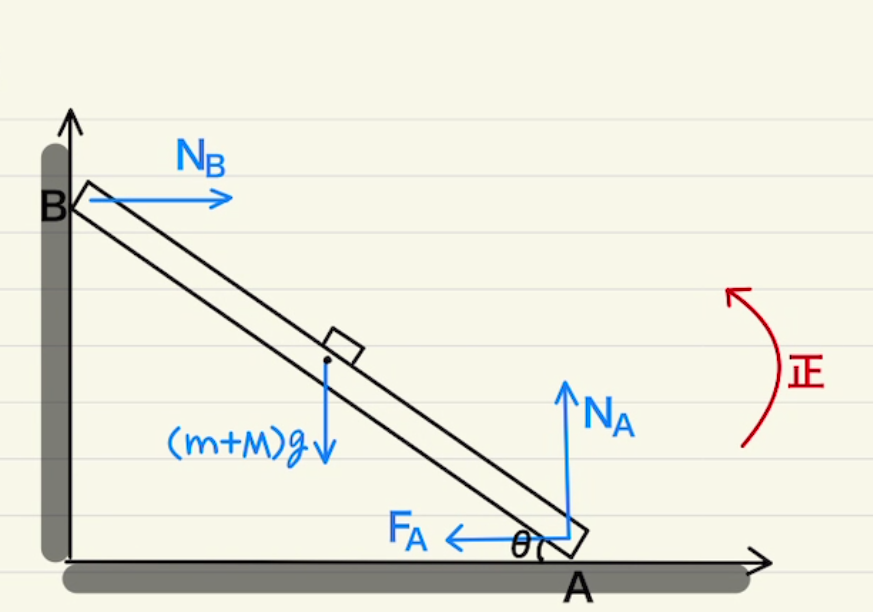
解答欄

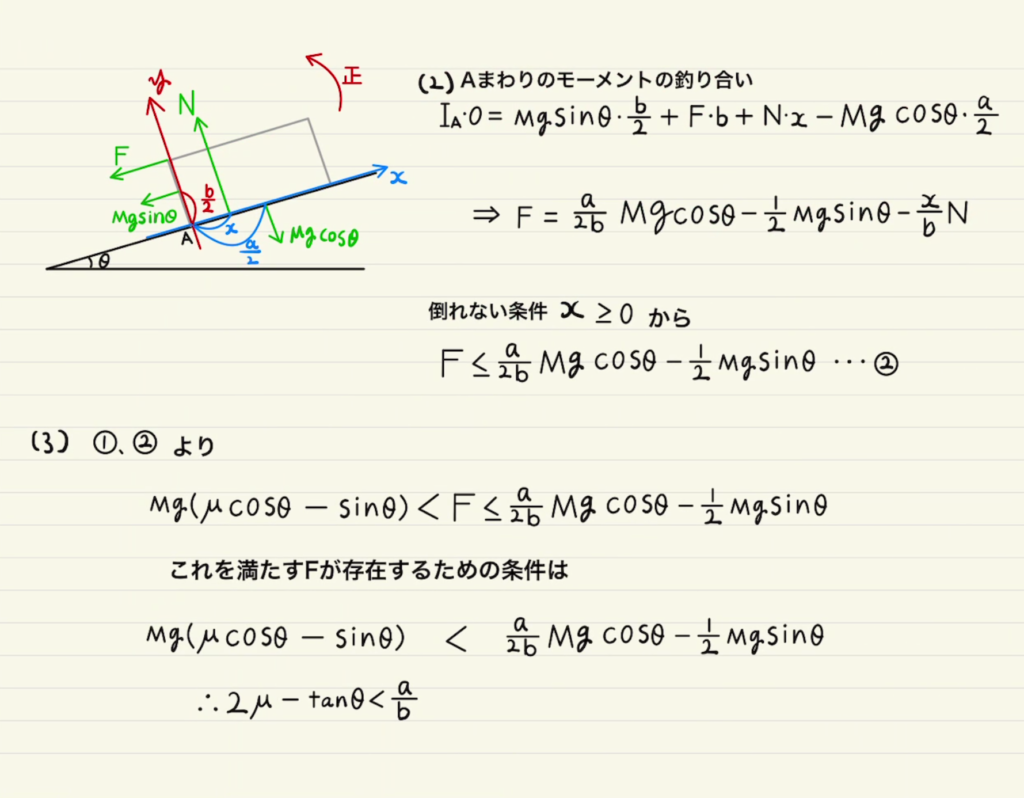
解説
今回は棒ではなく大きさのある物体であるため、平面で考えていかなければいけません。
そして、力のつり合いとモーメントのつり合いの二つの連立で条件を求めることができます。
モーメントのつり合いは、二つの方法で導けます。
一つ目は外積を使う方法です。$x-y$座標系を設定し、力のかかる位置ベクトル$r$と力ベクトル$f$の外積の合計は$0$になります。
式で表すと、$\sigma{\vec{r}×\vec{f}}=\vec{0}$となります。
見るべきは$z$成分だけになります。
このやり方の場合、機械的にできますが、計算が煩雑になりがちです。
二つめは力を$x,y$成分に分解し、$x$軸と$y$軸に力を投影するやりかたです。
今回はこのやり方で解説しています。
斜面に平行に$x$軸をとると、$F$と摩擦力$F_r$は $x$方向だけになり、垂直抗力$N$は$y$方向になるため、重力だけ成分分解する必要はあります。
(1)で滑る条件を調べ、(2)で回転しない条件を調べることによって、(3)で回転させずに滑らせることが可能にする条件を求める問題となっています。
つまり$b$が大きすぎると滑る前に転倒してしまうというというわけですね。
重要な点は力を強くしていくと、モーメントが釣り合うように垂直抗力$N$がどんどんAに近づいていって、Aまで届くと転倒してしまうという点です。
人間がつま先立ちしている状態と同じような感じですね。
このような点をゼロモーメントポイント(ZMP)と呼びます。