Lは$20[V]$までは非線形となっています。(おそらく、I=10^{-3}(V-20)^2+0.4)
それ以上の場合はV座標が2マス(20[V])進むごとにI座標は1マス(0.1[A])ことから、傾きは$ \frac{0.1}{20} $で線形的(直線)となっています。
(20[V],0.1[A])であることを使えば
$$I_L-0.4=\frac{0.1}{20}(V_L-20) (20≦V_L)$$
と表すことができます。$I_L$:フィラメントに流れる電流、$V_L$:フィラメント間の電圧差。
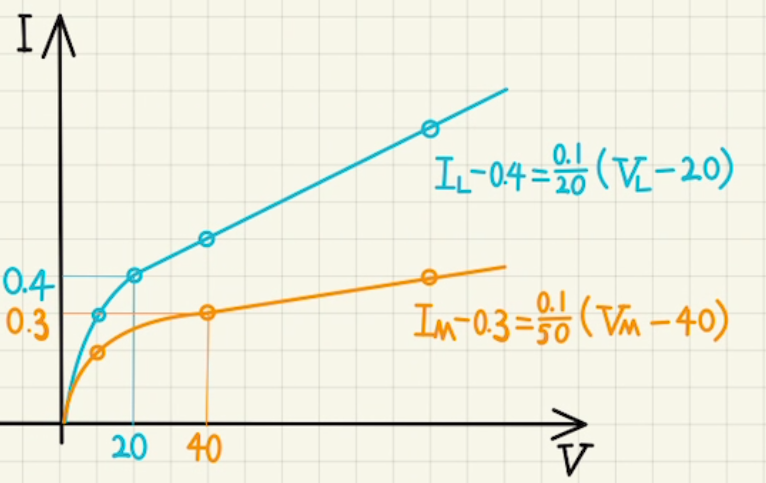
(1)Lに80Vの電圧をかけると、0.7[A]がながれるため、抵抗値は
$R_L(80)=\frac{V}{I}=1.1×10^2$
(2)
抵抗の温度係数$α$とは「温度が1℃変化したときの抵抗値の変化割合」です。
例えば、常温から温度が1℃上がったら抵抗値が0.1%上がった場合、$α=0.1×10^{-2}$となります。
常温で$R_0=1000[Ω]$の抵抗だった場合、1℃上がるごとに$αR_0=1[Ω]$ずつあがっていくことがわかりますね。
室温$T_0$の抵抗値を$R_0$とすると、温度$T$のときの抵抗値は以下のように表せます。
$$R(T)= R_0 + αR_0(T-T_0)$$
今回は$T_0=0[℃]$、$α=2.5×10^{-3}$、$R_0=20[Ω]$となるため、
$T=2.1×10^3$とかなりの高温になることがわかります。
(3)
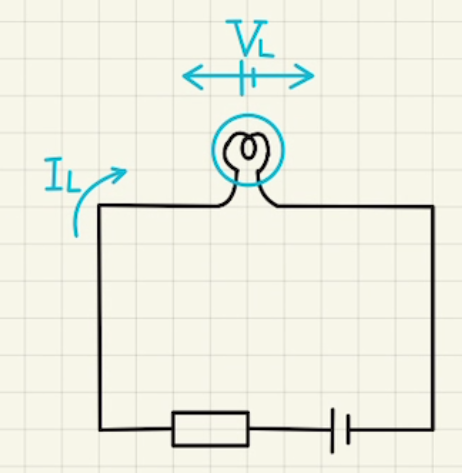
回路の式は
$E=RI_L+V_L$
となります。よって、電流は
$I_L=- \frac{1}{R} V_L+ \frac{1}{R} E$
となります。$E=120[V],R=100[Ω]$から、
$I_L=- 10^{-2} V_L+ 1.2$
これを図示すると下のようになります。
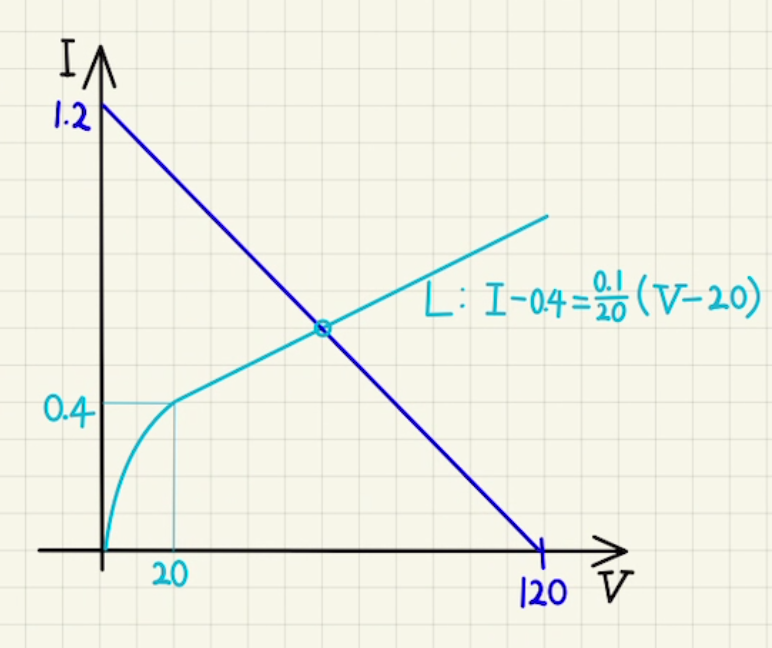
よって交点の部分の$(V_L,I_L)=(60,0.6)$がフィラメント間の電流と電位差になります。
消費電力$VI=36[W]$
・別解
$E=RI_L+V_L$
及び
$I_L-0.4=\frac{0.1}{20}(V_L-20) (20≦V_L)$
を同時に満たせばよいことになります。
$20≦V_L$を前提にすると、二式の連立により、
$(V_L,I_L)=(60,0.6)$ が求まります。
たしかに$20≦V_L$を満たしているので問題なさそうですね。
・補足
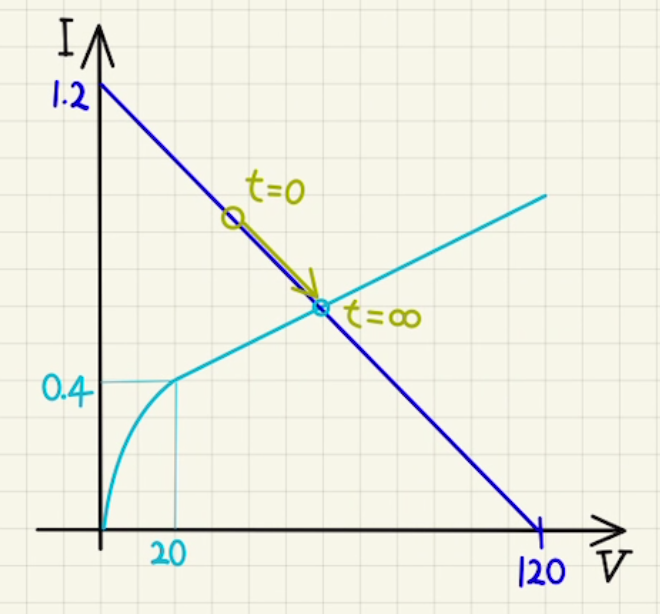
電流が流れた直後は室温での抵抗値$20[Ω]$に相当し、流れる電流は$I_0=\frac{120}{120+20}≈0.86[A]$の電流が流れます。
しかし、大きな電流が流れるとフィラメントが発熱し、それにともない抵抗値は上昇し電流は減少していきます。
最終的に収束する点が水色の曲線ということになります。
(4)
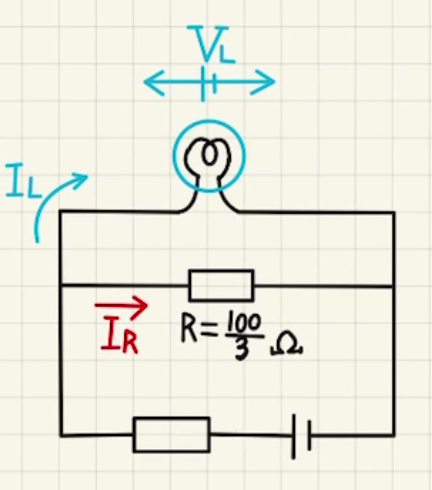
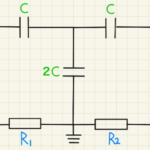
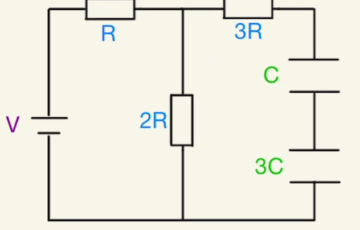
三つの抵抗には同じ電圧がかかるので、 $\frac{100}{3}[Ω]$の一つの合成抵抗として扱います。
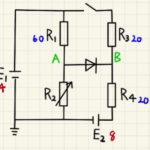
二つの回路の方程式は
$E=R(I_L+I_R)+V_L$
$E=R(I_L+I_R)+R’I_R$
これは$I_L,I_R$が未知数の連立方程式となります。
この連立方程式から$I_L$を求めると、
$I_L=- \frac{R+R’}{RR’} V_L+ \frac{E}{R} =-\frac{1}{25} V_L+1.2$
これを図示すると下の図になります。
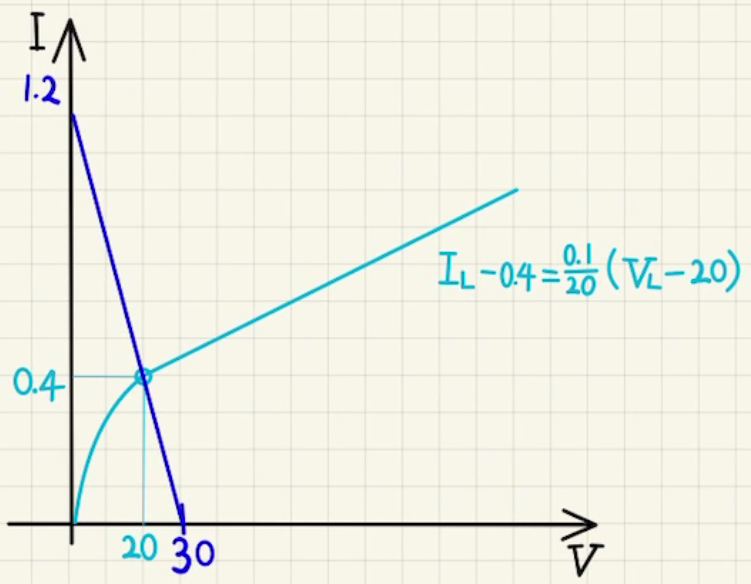
よって交点は
$(V_L,I_L)=(20,0.4)$となり、電圧は$V_L=20$
・別解
$I_L= -\frac{1}{25} V_L+1.2$
及び
$I_L-0.4=\frac{0.1}{20}(V_L-20) (20≦V_L)$
を同時に満たせばよいことになります。
$20≦V_L$を前提にすると、二式の連立により、
$(V_L,I_L)=(20,0.4)$ が求まります。
たしかに$20≦V_L$を満たしています。
(5)
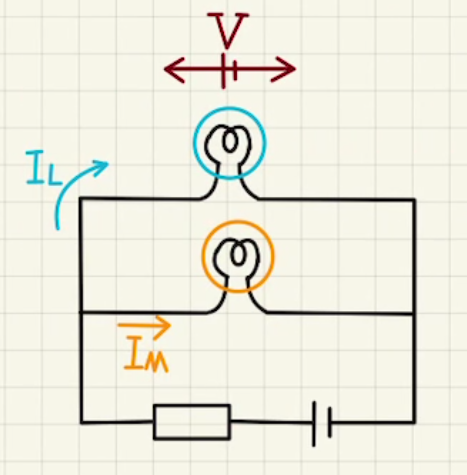
二つを連立させたとき、一つのフィラメント間の電位差を$V$とするともう一つも同じ電位差になるため、それぞれに流れる電流を足し合わせたものが電池から流れる電流 になるので、その電流と電位差の関係は以下の図になります。
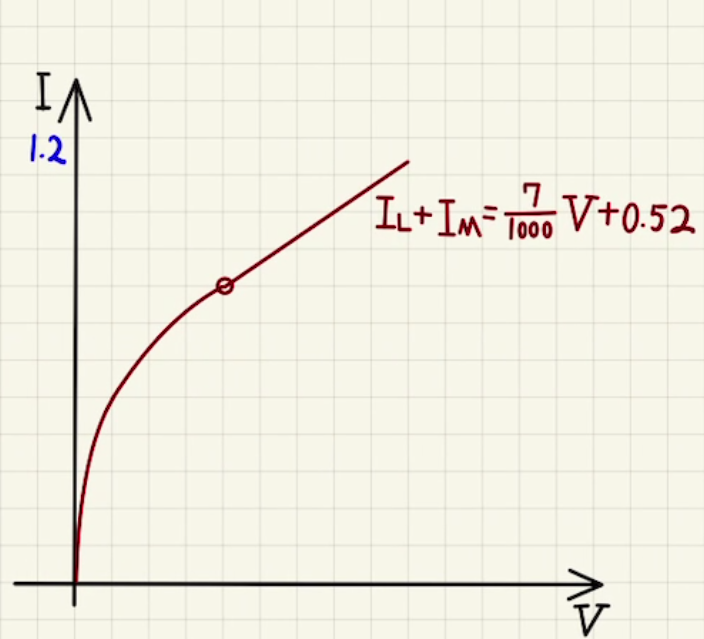
よって電池から流れる電流を$I$
$E=RI+V$
となります。よって、電流は
$I=- \frac{1}{R} V+ \frac{1}{R} E= – 10^{-2} V+ 1.2 $
これを図示すると、以下のようになります。
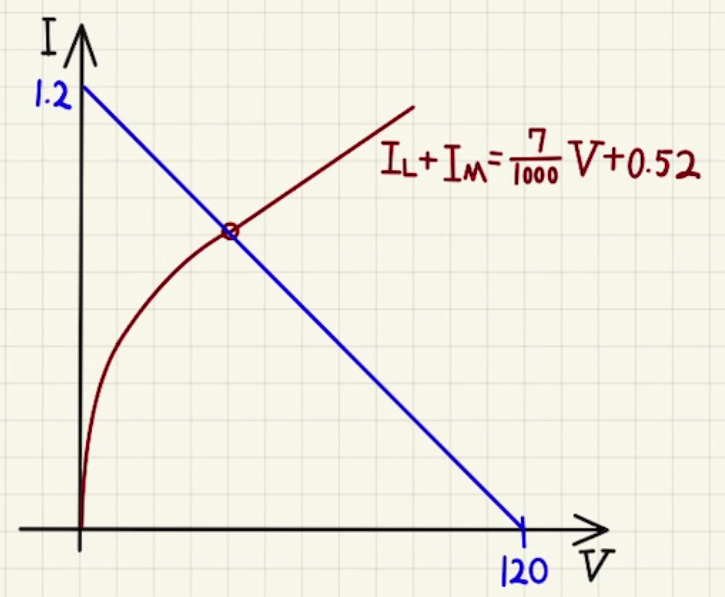
その交点から、 $(V,I)=(40,0.8)$
そのためフィラメントの電位差は、 $V=40$となります。
また、それぞれに流れる電流は$I_L=0.5, I_M=0.3$となります。
Lでの消費電力は$VI_L=20[W]$
全体での消費電力は電池のした仕事と等しく、$EI=96[W]$
・別解
図1から
$I_M-0.3=\frac{0.1}{50}(V_M-40) (40≦V_M)$
であるため、$V=V_L=V_M$として$I_L$の式と足し合わせると
$I_L+I_M-0.7=\frac{0.7}{100}(V-180) (40≦V)$
よって、
$I=I_M+I_L=\frac{0.7}{100}V+0.52 (40≦V)$
これと
$I= – 10^{-2} V+ 1.2 $
を同時に満たせばよいことになります。
$40≦V$を前提にすると、二式の連立により、
$(V,I)=(40,0.8)$ が求まります。
たしかに$40≦V$を満たしています。
(Q)
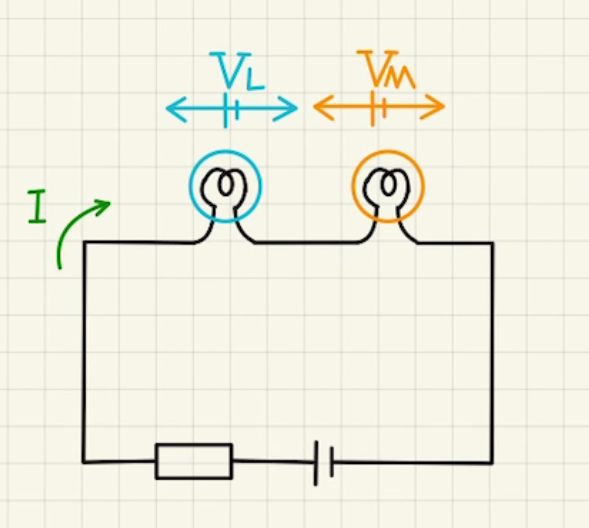
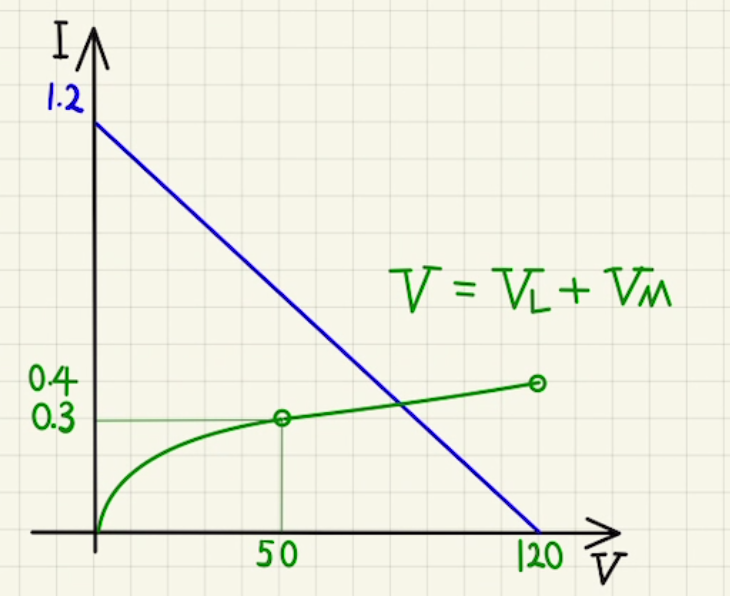
直列にした場合、二つのフィラメントには同じ電流が流れ、二つのフィラメント間の電圧は$V=V_L+V_M$となります。
つまり、$V$軸方向の足し算となるため、
回路の式は
$E=RI+V+V$
となるため、電流は
$I_L=- 10^{-2} V+ 1.2$
これを図示すると下のようになります。
$50≦V≦120$では直線ではないので正確には求められませんが、
その交点はおおよそ(85[V],0.35[A])となると言えます。
よって全体の消費電力は電池がした仕事と等しく、$W=EI=42[W]$