(1)
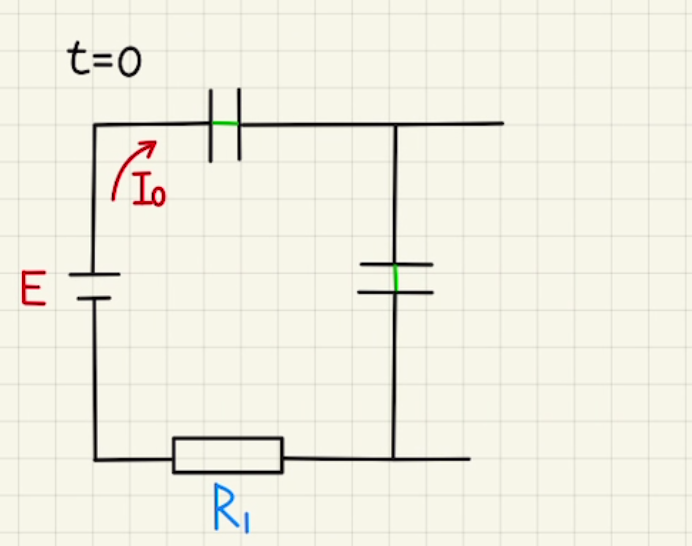
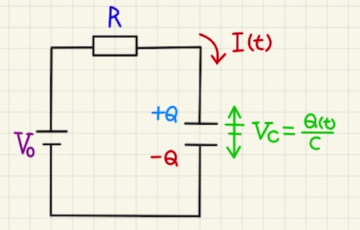
コンデンサーに電荷がたまっていないときは導線と同じように電流がそのまま流れていくので、
$E=R_1I_0$より
$I_0=\frac{E}{R_1}$
(2)
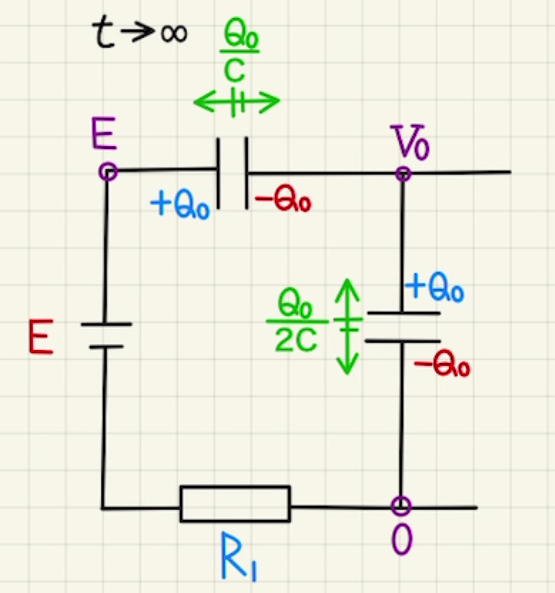
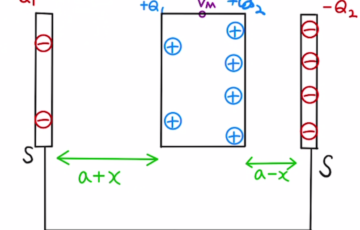
点Aは電気的に孤立しているため、電荷の合計は変わらないため、$C_1$と$C_2$にたまった電荷は等しくなります。
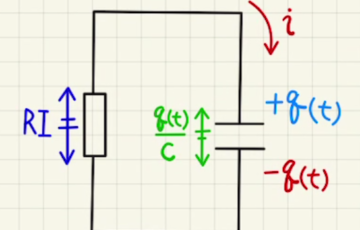
回路の方程式は
$E=\frac{Q_0}{C}+ \frac{Q_0}{2C} $
よって
$Q_0=\frac{2}{3}CE $
電位は
$V_0=\frac{Q_0}{2C}=\frac{1}{3}E $
(3)
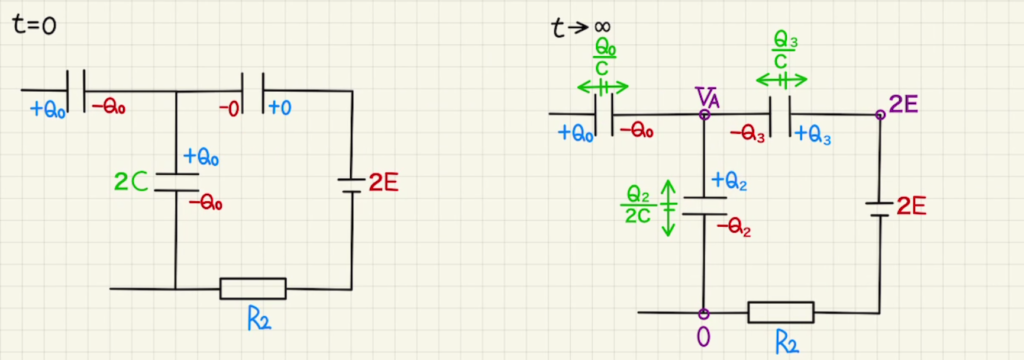
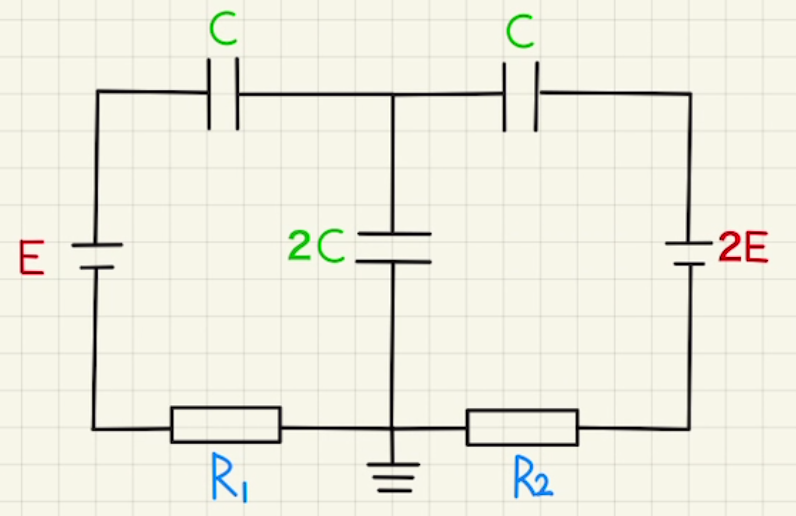
右図の回路の方程式は
$$2E= \frac{Q_2}{2C} + \frac{Q_3}{C} ① $$
未知数は$Q_2, Q_3$の二つなのでこの式だけでは解けません。
そのため、孤立した部分の電荷の保存も使います。
Bは孤立しているため、$C_1$にたまった電荷は$Q_0$のまま変わりません。
また、孤立しているAも電荷の合計は変わらず、
$$-Q_0+Q_2-Q_3=0 ②$$
よって①,②の連立になります。
②より$ Q_3 =Q_2-Q_0$となるため、これを①に代入すると、
$2E= \frac{Q_2}{2C} + \frac{ Q_2-Q_0 }{C} $
よって
$$Q_2= \frac{1}{3}(4CE+2Q_0)= \frac{16}{9}CE$$
以上より、
$$V_A= \frac{Q_2}{2C}= \frac{8}{9}CE $$
$$V_B= V_A + \frac{Q_0}{C}= \frac{14}{9}CE $$
(4) $Q_3= Q_2-Q_0= \frac{10}{9}CE $
(5)$上げた電位×電荷量$が電荷にした仕事になります。
よって電池のした仕事は$W_E=2E×Q_3$となり、エネルギー保存は
($t=0$での$C_2$のエネルギー)+($t=0$での$C_3$のエネルギー)+(電池のした仕事)ー(抵抗で消費された電力)=($t=∞$での$C_2$のエネルギー)+($t=∞$での$C_3$のエネルギー)
となるため、抵抗で消費された電力を$W_R$とすると
$$ \frac{Q_0^2}{2C} + \frac{0^2}{C} + 2EQ_3 – W_R= \frac{Q_2^2}{2C} + \frac{Q_3^2}{C} $$
これを計算すると、
$$ W_R = \frac{25}{27} CE^2 $$
(6)
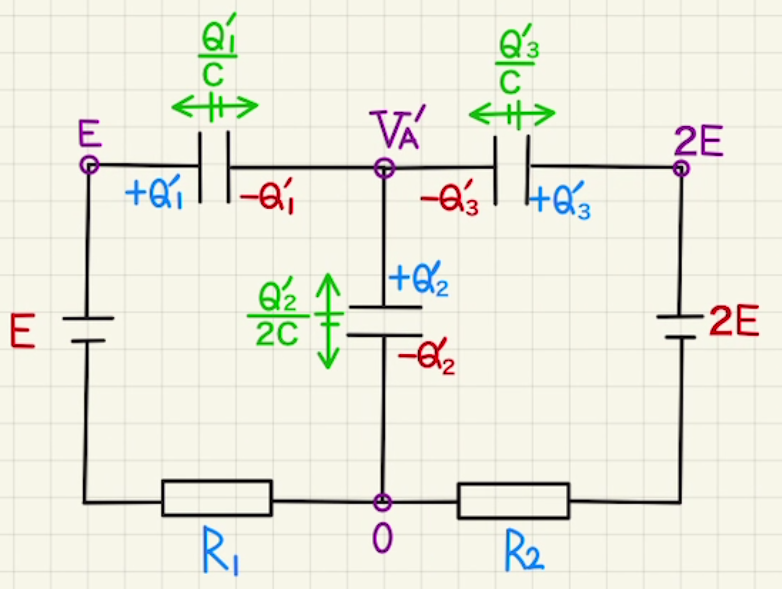
十分に時間が経った後は電流が流れていないと考えます。
左部分の回路の方程式は
$$E= \frac{Q’_1}{C} + \frac{Q’_2}{2C} ①’$$
右側の回路の方程式は
$$2E= \frac{Q’_3}{C} + \frac{Q’_2}{2C} ②’$$
未知数は$Q’_1,Q’_2, Q’_3$の三つなのでこの二式だけでは解けません。
そのため、今回も孤立した部分の電荷の保存も使います。
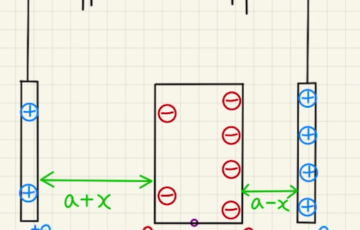
Aは孤立しているため、
$$-Q’_1+Q’_2,-Q’_3=0 ③’$$
この ①’ ②’ ③’ 式を連立して解くと、
$$Q’_1=\frac{1}{4}CE$$
$$Q’_2=\frac{3}{2}CE$$
$$Q’_3=\frac{5}{4}CE$$
となるため、
$$V’_A=\frac{ Q’_2 }{2C}= \frac{3}{4}E$$
となることがわかりました。
(5)別解
エネルギー保存則ではなく、時間変化から求めていくこともできます。

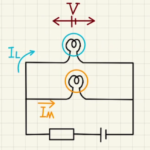
時刻$t$に流れるで流れる電流を図の向きに$i$とします。
すると、回路の方程式は
$$2E= \frac{q_2}{C}+ \frac{q_3}{2C} +R_2i$$
となります。
$C_2,C_3$のコンデンサーも$i$で流れてきた電流が電荷となるため、$\frac{dq_2}{dt}=i$及び $\frac{dq_3}{dt}=i$となります。
これを用いて回路の式を時間で微分すると、
$0=\frac{i}{C}+ \frac{i}{2C} +R_2\frac{di}{dt}$
これを書き換えると、
$$\frac{di}{dt}=-\frac{3}{2R_2C}i$$
この微分方程式は空気抵抗と同じ式であり、変数分離で解くことができます。
$\frac{di}{i}=-\frac{3}{2R_2C}dt$
これを積分すると、積分定数をAとし、
$\log{i}=-\frac{3}{2R_2C}t+A$
両辺を$e^{〇〇}$に入れると
$i=e^{A}e^{-\frac{3}{2R_2C}t}$
積分定数は$e^{A}=i_0$と置き換えることができ、
$$i=i_0e^{ -\frac{3t}{2R_2C}}$$
この$i_0$は初期電流であり、
$2E=R_2i_0- \frac{Q_0}{2C}$より、
$i_0=\frac{5E}{3R_2}$とわかります。
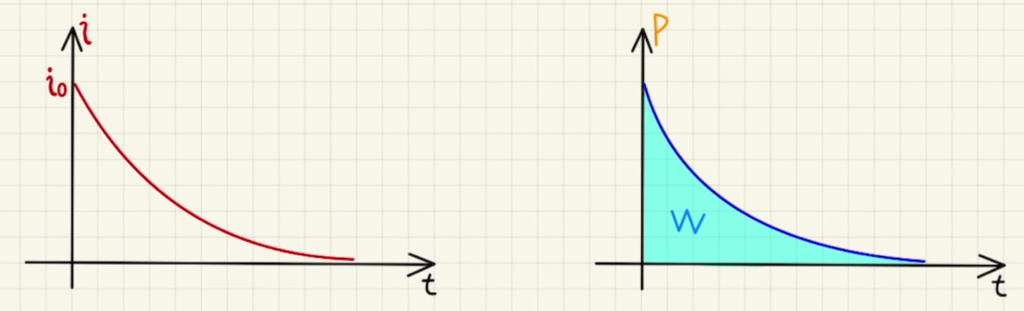
今、$R_2$での時間当たりの消費電力$P$が
$$P=R_2i^2=\frac{25E^2}{9R_2} e^{ -\frac{3t}{R_2C}} $$
なので、
$$W_R=\int_0^∞{Pdt}=\left[-\frac{25CE^2}{27} e^{ -\frac{3t}{R_2C}}\right]_0^∞= \frac{25}{27} CE^2 $$