今回の問題ではわかる数値から一つずつ出していくほうが楽ですが、解き方全体像を見るために電圧から全ての電流値を計算していきます。
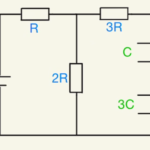
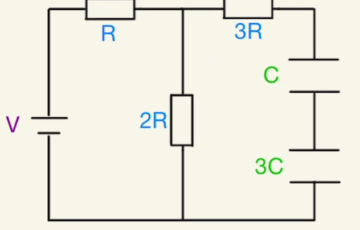
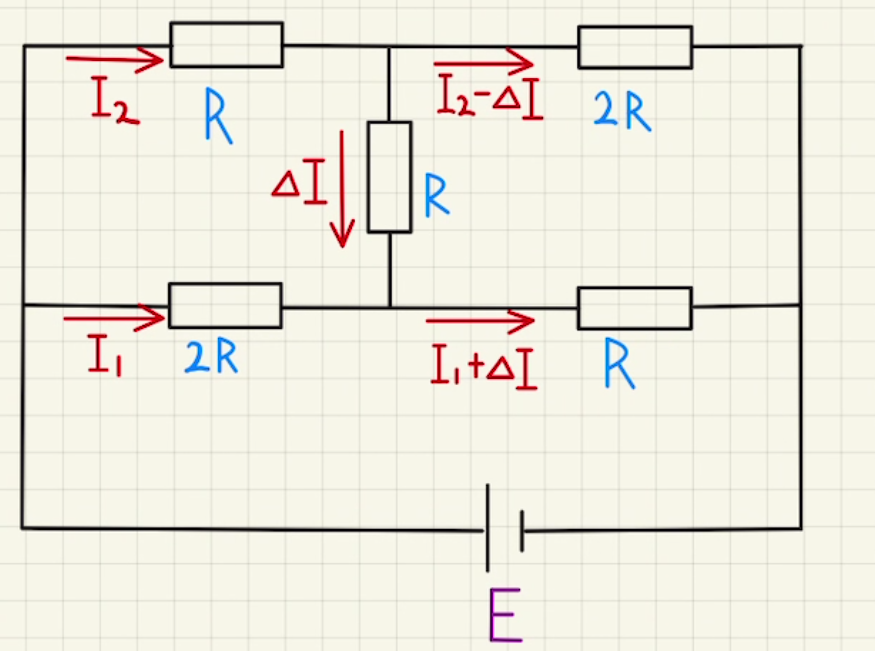
そのために、三つの閉回路に対してキルヒホッフを適用します。

まず上の経路での方程式は
$E=RI_2+2R(I_2-ΔI)$
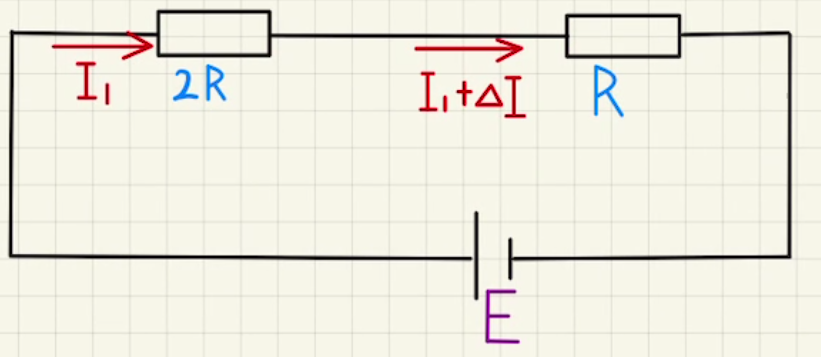
次に下の経路を通った場合の方程式は
$E=2RI_1+R(I_1+ΔI) ②$
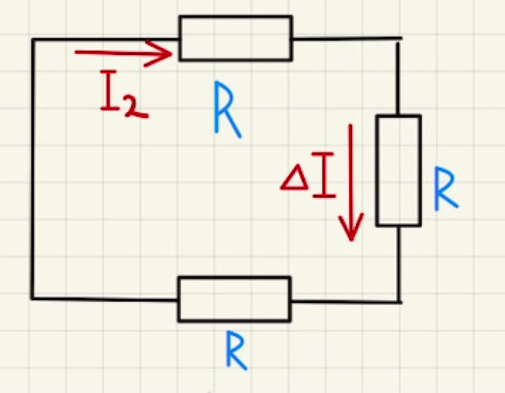
そして最後は左上の閉回路を見てみる
このときの方程式は
$0=RI_2+RΔI-2RI_1 ③$
これらの三つの式から三つの電流の値を求めることができます。
$$I_1=\frac{2}{7} \frac{E}{R} $$
$$I_2=\frac{3}{7} \frac{E}{R} $$
$$ ΔI=\frac{1}{7} \frac{E}{R} $$
(2) ΔI=\frac{1}{7} \frac{E}{R}及び$R=1[kΩ]、ΔI=1[mA]$から
$E= \frac{7}{1}RΔI=7[V] $
(1)$I_1= \frac{2}{7} \frac{7}{1}= 2[mA]$
(3)$I_1= \frac{3}{7} \frac{7}{1}= 3[mA]$
(4)

中央部分の電位が同じになるようにするには、それぞれの抵抗の比を同じにすればよく。
$R:2R=2R:R_D$
よって求めるべき抵抗は$R_D=4R=4[kΩ]$
補足
(4)も未知の抵抗値を$R_D$と置いて、三つの回路の方程式を求めることによって、$ΔI$の値を$R_D$の関数として求めることができます。
このとき$ΔI$が0となる条件から$R_D$が求まります。
こちらのほうが計算が面倒ですが、本来の解き方に近いでしょう。