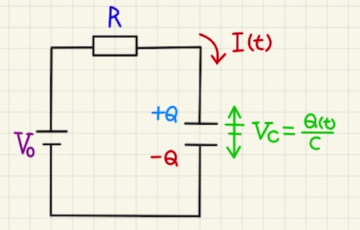
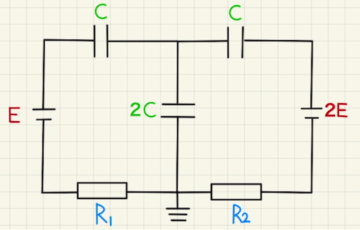
(1)最初はLM間もMN間のコンデンサーも電気容量も等しく板の面積を$S$とすると
$C_0=ε\frac{S}{a}$
となります。
よってMにたまった電荷は
$Q_M=2Q_0=2C_0V_0$
(2)
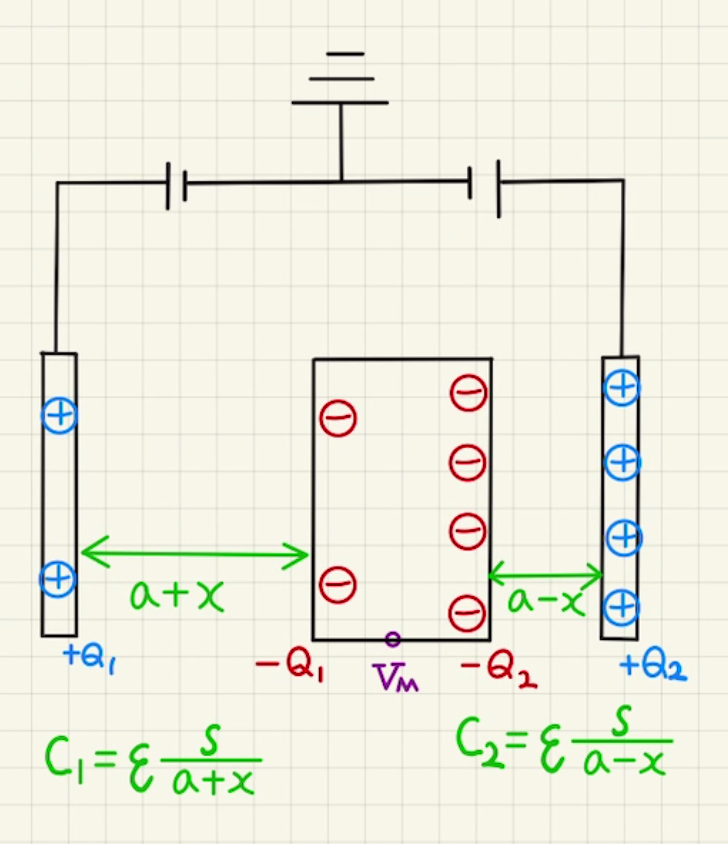
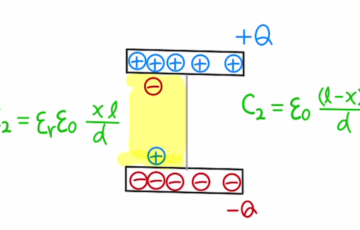
$C_1= ε\frac{S}{a+x} = \frac{a}{a+x}C_0$
$C_2= ε\frac{S}{a-x} = \frac{a}{a-x}C_0 $
(3)
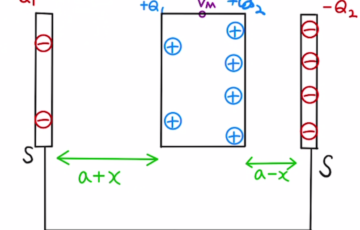
中央の電位を$V_M$とすると、両端にたまった電荷は
$Q_1= C_1(V_0-V_M) = \frac{a}{a+x}C_0 (V_0-V_M) $
$Q_2= C_2(V_0-V_M) = \frac{a}{a-x}C_0 (V_0-V_M) $
この電荷が板Mで保存するため、
$-Q_1- Q_2 = -2Q_0$
よって
$\frac{a}{a+x}C_0 (V_0-V_M) + \frac{a}{a-x}C_0 (V_0-V_M) = 2C_0V_0 $
よって
$V_M=\frac{x^2}{a^2}V_0$
$Q_N=+Q_2= \frac{a}{a-x}C_0 (V_0-V_M) =\frac{a+x}{a}C_0V_0$__答
$Q_L=+Q_1= \frac{a}{a+x}C_0 (V_0-V_M) =\frac{a-x}{a}C_0V_0$
(4) $V_M=\frac{x^2}{a^2}V_0$
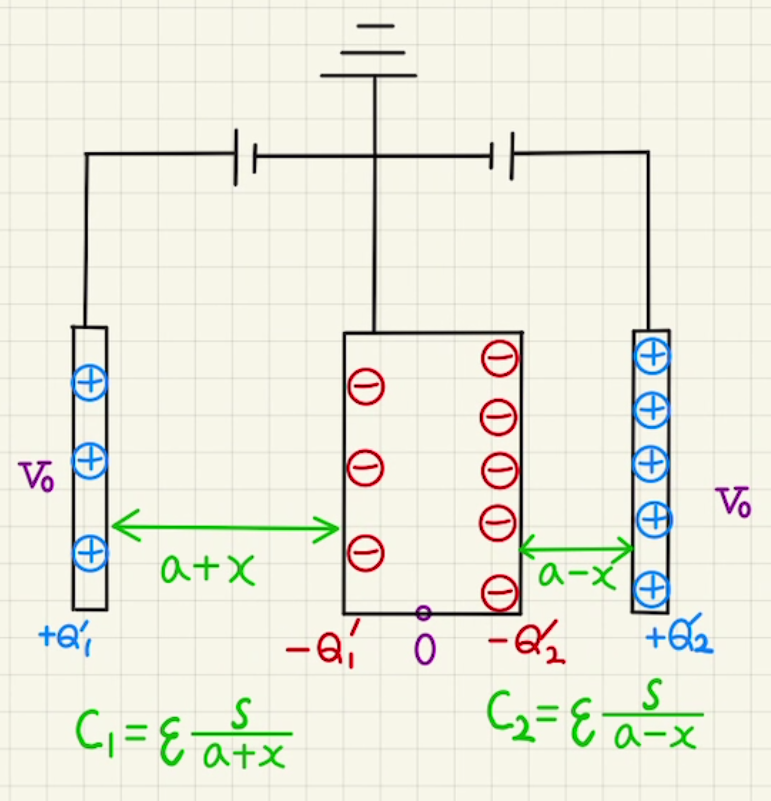
(5)再び通電するとMの電位は$0$となり、それぞれに帯電した電荷は
$Q’_1= C_1V_0 = \frac{a}{a+x}C_0V_0 $
$Q’_2= C_2V_0 = \frac{a}{a-x}C_0V_0$
つまり、Mの電荷が$Q_M = -Q_1- Q_2 $から$Q’_M=-Q’_1- Q’_2$になります。
よってMに流れ込んだ電気量は
\begin{align}
Q’_M – Q_M &= (-\frac{a}{a+x}C_0V_0 – \frac{a}{a-x}C_0V_0)-( \frac{a-x}{a}C_0V_0 + \frac{a+x}{a}C_0V_0 )\\
&= -\frac{2x^2}{a^2-x^2}C_0V_0
\end{align}
よって電荷は$M$から$ \frac{2x^2}{a^2-x^2}C_0V_0 $だけ出ていく。
(6)
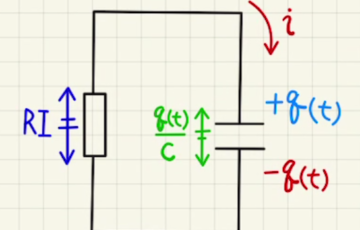
スイッチを開いている間はNの電荷は
$$Q_N= \frac{a+x}{a}C_0V_0= \frac{C_0V_0}{a}x + C_0V_0 $$
で推移するため、Nに流れ込む電流は
$$\frac{dQ_N}{dt}= \frac{C_0V_0}{ a} \frac{dx}{dt}= \frac{C_0V_0}{ a}v $$
・補足
スイッチが閉じている状態で動かすとどれだけ電流が流れるかも考えてみましょう。
スイッチを 閉じている間はNの電荷は
$Q_N= \frac{a}{a-x}C_0V_0 = -C_0V_0a \frac{1}{x-a} $
で推移するため、Nに流れ込む電流は
\begin{align}
\frac{dQ_N}{dt} &= \frac{ dQ_N }{dx} \frac{dx}{dt}\\
\phantom{ \frac{dQ_N}{dt} } &= -C_0V_0a \frac{ d }{dx}\left( \frac{1}{x-a}\right) \frac{dx}{dt}\\
\phantom{ \frac{dQ_N}{dt} } &= C_0V_0 \frac{a}{(x-a)^2}v
\end{align}
となり、$ \frac{a}{(x-a)^2} > \frac{1}{a} (x>0)$から、スイッチを入れたほうがより多くの電流が流れることがわかります。
(Q)
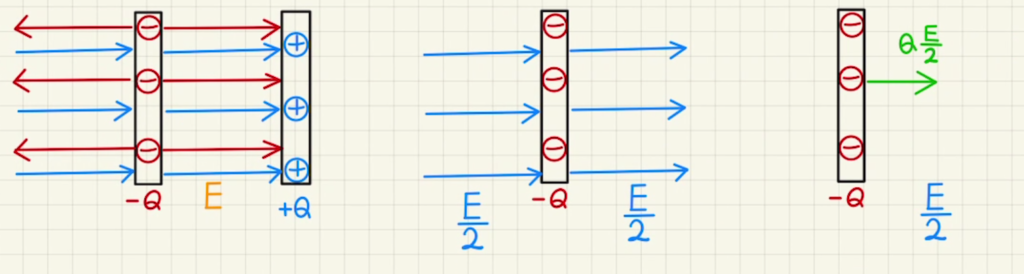
電荷$Q$をたまったコンデンサーでは、電場$E=\frac{V}{d}$が発生します。
しかし、左の電極版(赤)の位置では、自分側の電極版が発生させる電場は両方向に発生して打ち消しあっているため、もう一方の電極版(青)の影響のみ受けます。
そのため、受ける力は$f=\frac{1}{2}QE $となります。
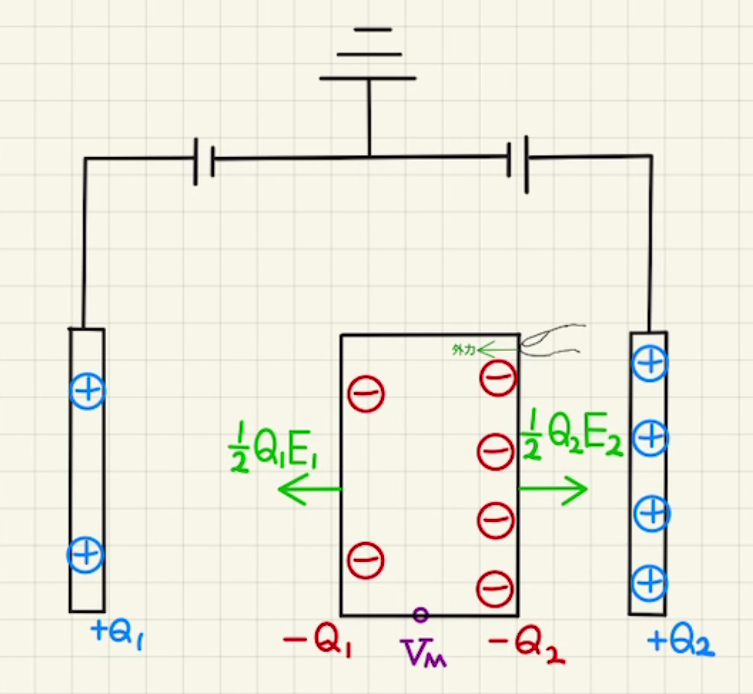
ここから、Mが受ける力は右方向に
\begin{align}
F &= \frac{1}{2}Q_2E_2 – \frac{1}{2}Q_1E_1 \\
&= \frac{1}{2}Q_2\frac{Q_2}{a-x} – \frac{1}{2}Q_1\frac{Q_1}{a+x} \\
&=\frac{2x}{a^2}C_0V_0^2
\end{align}
よって一定速度で動かすためには外力を反対の方向である左側に、同じだけ与える必要があります。