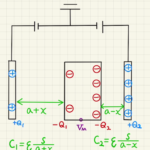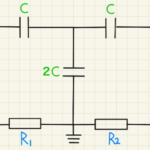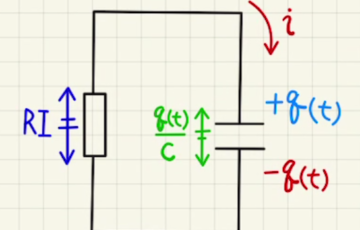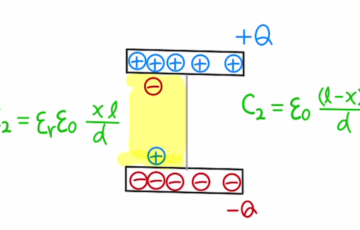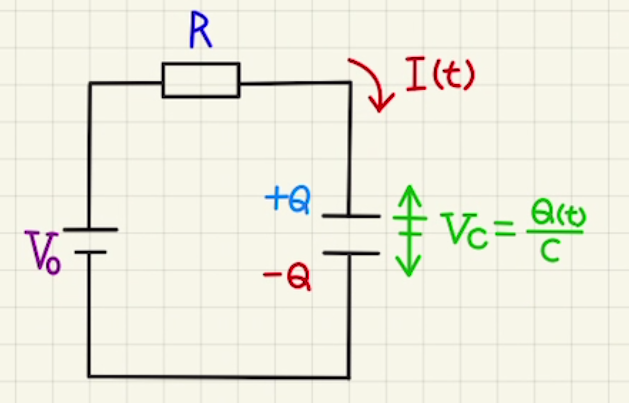
電池と抵抗によるコンデンサーの充電や、放電は指数関数の形で変化していきます。
詳しくはコンデンサーの電荷の変化をご覧ください
今回は回路の方程式が
$$V=RI(t) + \frac{Q(t)}{C} $$
となることから、コンデンサーの電荷を計算していくと
$$Q(t)= CV_0(-e^{-\frac{1}{CR} t} + 1)$$
が求められます。
これを時間微分することで
$$I(t)= \frac{V_0}{R}e^{-\frac{1}{CR} t}$$
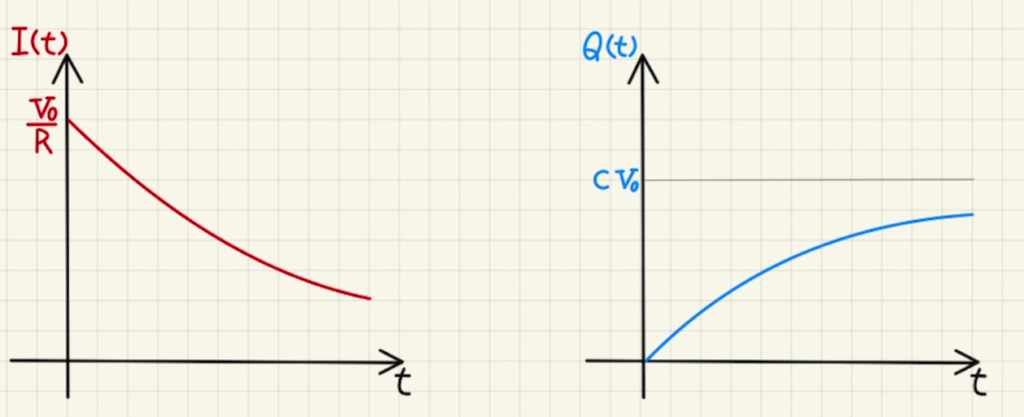
知っておくと便利ですが、問題はそれを使わなくても求めることはできます。
(1)時刻tの時の回路の方程式は
$$V_0=RI(t)+V(t)$$
となるため、
$$ I(t) =\frac{1}{R}(V_0-V)$$
(2)
電流が半分になる時刻t_2とすると、流れる電流は時刻t=0のときの$\frac{1}{2}$なので
$$I(t_2)=\frac{1}{2} I(0)= \frac{1}{2R}V_0 $$
となります。
これを(1)の式にと比較すると
$$\frac{1}{R}(V_0-V) = \frac{1}{R}V_0 $$
よってコンデンサー間の電圧は
$$V= \frac{1}{2}V_0 $$
となるため、たまった電荷は
$Q=CV= \frac{1}{2}CV_0 $
となります。
(3)
(ア)t=0のとき、
$$ I(0) =\frac{1}{R}V_0$$
$$R=\frac{V_0}{I(0)} =\frac{4.0}{1.6×10^{-3}}=2.5×10^3[Ω]$$
(イ)1マスあたり
$0.1×10^{-3}[A]×1[s]=1.0×10^{-4}[C]$
ということができます。
電流が半分になるまでに流れた電流を積分すると、コンデンサーにたまった電荷になるため
$$ Q(t_2)=\int_{t=0}^{t=t_2}(Idt)=100×1.0×10^{-4}=1.0×10^{-2}[C]$$
これを$t=0,t_2,∞$のときと比較すると、
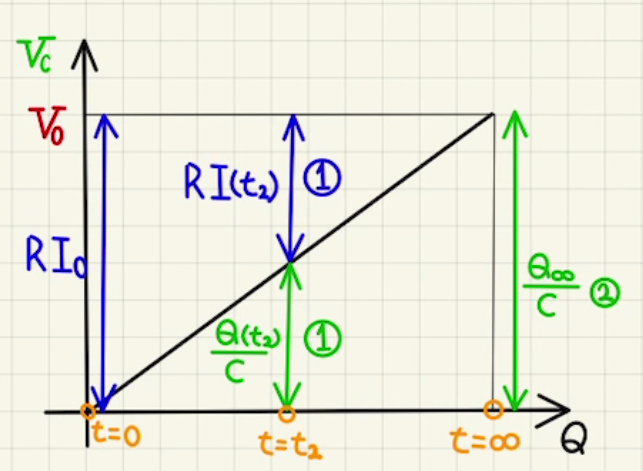
$t=t_2:V_0=R\frac{I(0)}{2}+\frac{Q(t_2)}{C}$
$t=∞: V_0=R×0+\frac{Q_∞}{C}$
よって、電流比が$2:1:0$のとき、コンデンサーの電荷比は$0:1:2$になります。
よって
$$Q_∞=Q(t_2)=2.0×10^{-2}[C]$$
また、
$$ C=\frac{Q_∞}{V_0}=5.0×10^{-3}[C/V]$$
・補足
$$I(t)= \frac{V_0}{R}e^{-\frac{1}{CR} t}$$
が$t=0$のときの半分である$\frac{V_0}{2R}$となるのは
$$e^{-\frac{1}{CR} t}=\frac{1}{2}$$
このとき、$t≒9.0$なので
$$C=\frac{t}{Rlog2}≒\frac{9.0}{6.4×0.7}≒5.1×10^{-2}$$
と近い値がでました。
(4)
それぞれの$t=0$での電流を比較すると
$$ I(0) =\frac{1}{R}V_0$$
$$ I'(0) =\frac{1}{R’}V_0$$
で、$I'(0)=\frac{1}{2}I(0)$より、$R’$は$R$の2倍となることがわかります。
また、最終的に$t=∞$で貯められる
$$ Q_∞=\int_{0}^{∞}Idt$$
$$ Q’_∞=\int_{0}^{∞}I’dt$$
より、 $I’$は常に$I$の$\frac{1}{2}$倍であることから$Q’$は$\frac{1}{2}$倍となります。
よって$C$も$\frac{1}{2}$倍ということがわかります。
・別解
電流は
$$I(t)= \frac{V_0}{R}e^{-\frac{1}{CR} t}$$
でした。
しかし、抵抗と電気容量を$R’,C’$に変えたとき、流れる電流が常にその半分でした。
そのため、流れる電流は
$$I'(t)= \frac{V_0}{R’}e^{-\frac{1}{C’R’} t} = \frac{1}{2}\frac{V_0}{R}e^{-\frac{1}{CR} t}$$
となります。
つまり$e^{〇}$の係数部分$\frac{V_0}{R’}$が半分で、中身の(tの係数)$-\frac{1}{CR}$が同じでなくてはいけません。
よって
$$\frac{V_0}{R’}=\frac{V_0}{2R}$$
$$-\frac{1}{C’R’} =-\frac{1}{CR}$$
このことから
$$R’=2R$$
$$C’=\frac{1}{2}C$$