モーメントと言われてまず何を想像するでしょうか。
小中学校でやった”てこの原理”がまず思い浮かぶ人が多いと思います。
そのシンプルな図から始めます。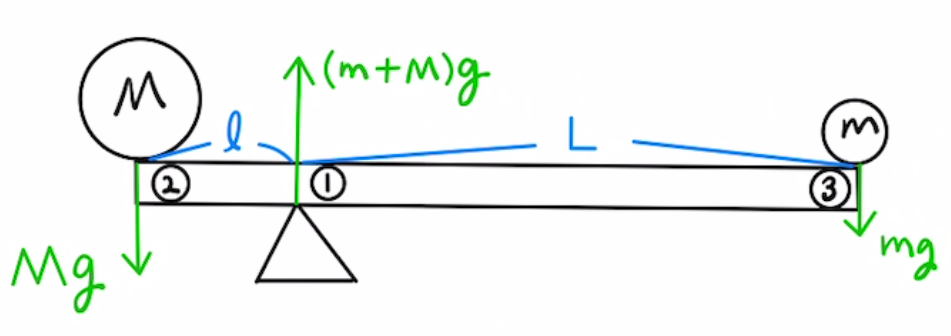
この図では回転しないために支点周りに$Mg×l = mg×L$が成り立たないといけないはずでしたね。
今回は支点を中心とした回転を見ていましたが、他の部分を中心とした回転で見てもいいのではないでしょうか?
答えは、どこの点をとってもいいです。
実際に①、②、③のそれぞれの点を中心としたモーメントのつり合いの式を立てることができます。
①$ Mg×l = mg×L $
②$ (m+M)g×l = mg×(l+L) $
③$ (m+M)g×L = Mg×(l+L) $
このように「どの点を取ってもモーメントのつり合いを見ることができる」というのが一つの大事な点となります。
ここからより話を一般化してみましょう。
モーメントの方程式
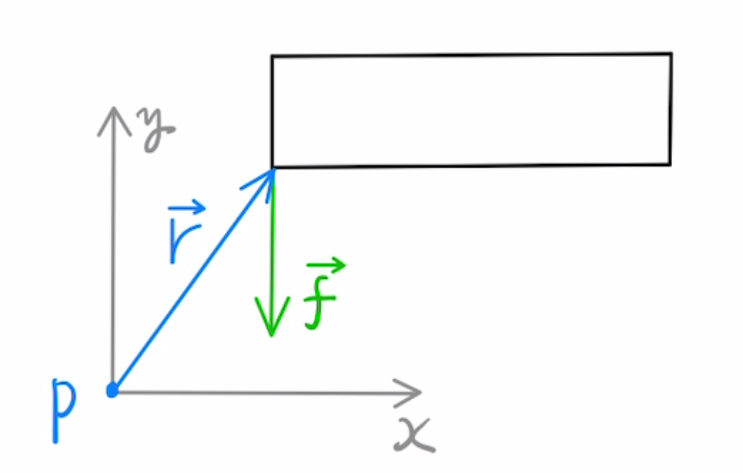
ある任意の点$P$周りのモーメントの方程式は以下のようになります。
$$I\vec{\dot{ω}} = \vec{r} × \vec{f} $$
一見するとわかりにくい式となっているのですが、運動方程式
$$m\vec{a} = \vec{f}$$
と非常に似ています。
$I$:慣性モーメント,回転のしにくさ
$m$:質量、動きにくさ
$ \vec{\dot{ω}} $:各加速度、より回転を速くする度合い
$\vec{a}$:加速度、より速度を速める度合い
$ \vec{r} × \vec{f} $:モーメント ( $\vec{r}$は位置ベクトル)
$ \vec{f} $:力
という対応関係になっています。
慣性モーメントは物体の形と質量及び点Pの位置で定まります。
$I=\int{r^2dm}$で定義されるのですが、高校範囲で使うことは、まずありません。
というのもモーメントのつり合いの場合は$ \vec{\dot{ω}} = \vec{0} $となる場合しか考えず、方程式は
$$\vec{0} = \vec{r} × \vec{f} $$
となるからです。
そのため、考えるべきは右辺のモーメントの式になります。
一つずつ見ていきましょう。
モーメントは位置と力の外積
ベクトルの外積の定義は
$$\begin{bmatrix} x \\y \\z \end{bmatrix}× \begin{bmatrix} f_x \\f_y \\f_z \end{bmatrix} = \begin{bmatrix} yf_z-zf_y \\ zf_x-xf_z \\ xf_y-yf_x \end{bmatrix} $$
となります。
ベクトルの内積はベクトルではありませんが、外積の結果はベクトルになります。
計算式はなにを意味しているかというと、$ \vec{r}$と$\vec{f}$のどちらにも垂直なベクトルが外積となります。
また、二つのベクトルのなす角度を$θ$とすると、外積の絶対値(大きさ)には以下の特性があります。
$$|\vec{r} × \vec{f}| = |\vec{r}| |\vec{f}| \sin{θ} $$
内積の場合 $\cos{θ} $なので、その逆ですね。
$θ=0$つまり二つのベクトルが水平の時は0になります。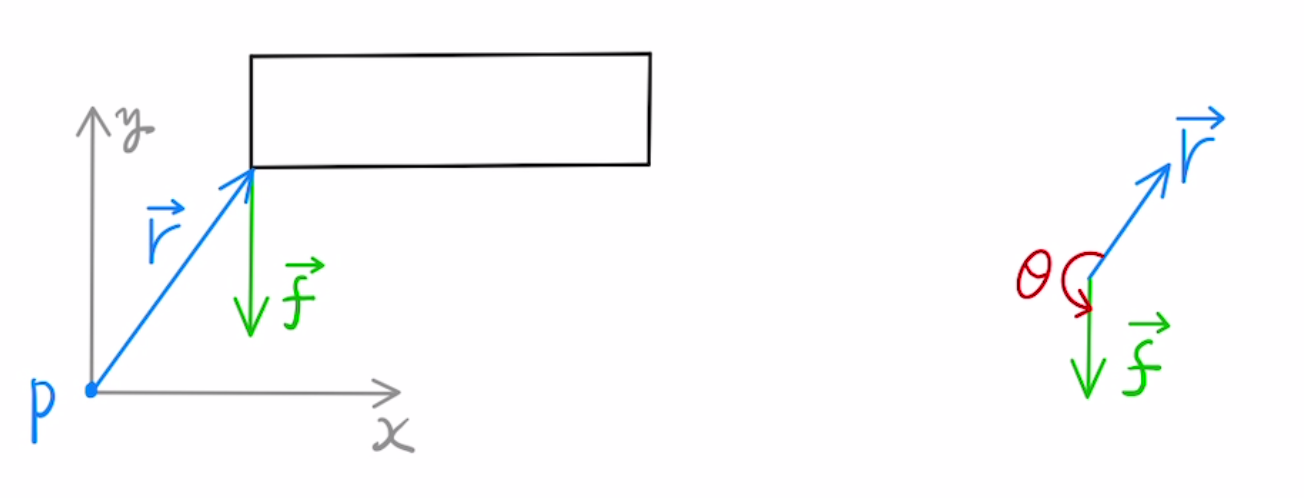
ちなみに二つのベクトルのなす角度とは、図のように始点を揃えて $\vec{r} $から $\vec{f} $に左回りに角度を測ったものです。
モーメントはベクトル
モーメントは外積なので、計算結果もベクトルの形になります。
これはなにを意味しているのでしょうか。
モーメントの$x$成分はx軸と平行な芯を中心にしたモーメントとなります。
つまり、$yz$平面での回転ですね。
同様にモーメントの$y$成分は$xz$平面での回転、モーメントの$z$成分は$yz$平面での回転
多くの問題では$xy$平面の回転だけを考えるため、モーメントは$z$以外0になります。
$$M_z = xf_y-yf_x$$
が$0$になればいいということになります。
複数の力がかかる場合は全てのモーメントを合計する
運動方程式で合力(力の合計)を使ったように、今回もモーメントの合計を使うことになります
モーメントのつり合いの式の右辺は、全てのモーメントの合計であり、一般化した式は下のようになります。
$$\vec{0} = \sum{\vec{r} × \vec{f}} $$
図でいうと
$$\vec{0} = \vec{r_1} × \vec{f_1} + \vec{r_2} × \vec{f_2} + \vec{r_3} × \vec{f_3} $$
成分表示にすると下のようになります。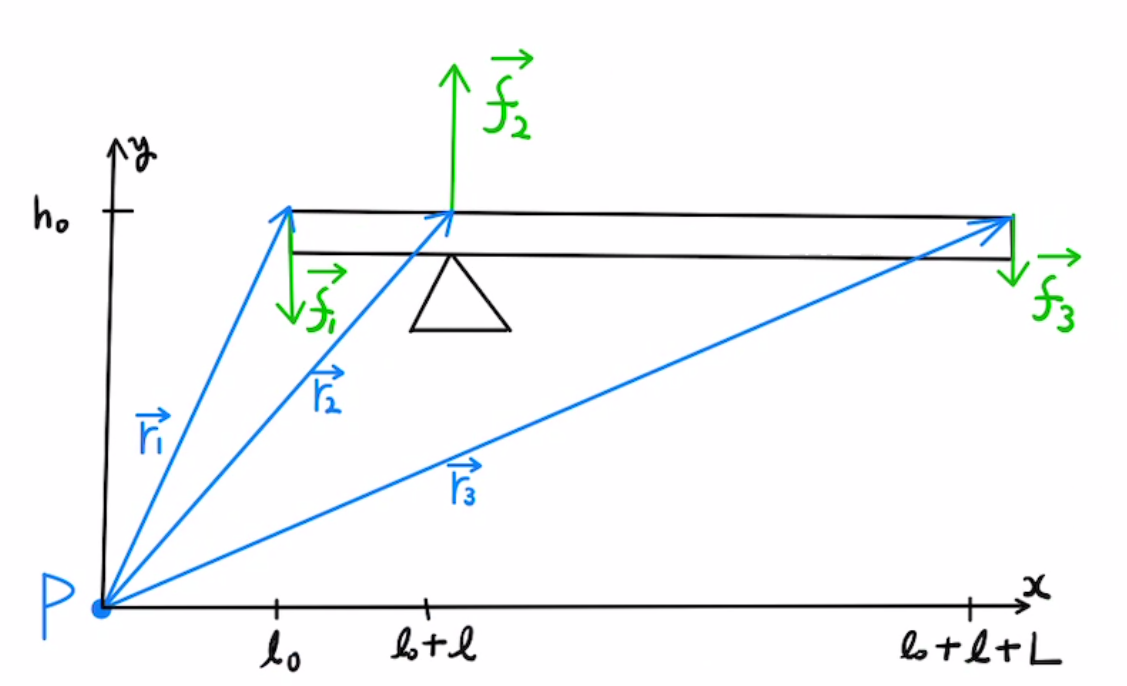
$$ \begin{bmatrix} 0 \\0 \\0 \end{bmatrix} = \begin{bmatrix} l_0 \\h_0 \\0 \end{bmatrix}× \begin{bmatrix} 0 \\-Mg \\0 \end{bmatrix} + \begin{bmatrix} l_0+l \\h_0 \\0 \end{bmatrix}× \begin{bmatrix} 0 \\(m+M)g \\0 \end{bmatrix} + \begin{bmatrix} l_0+l+L \\h_0 \\0 \end{bmatrix}× \begin{bmatrix} 0 \\-Mg \\0 \end{bmatrix} $$ 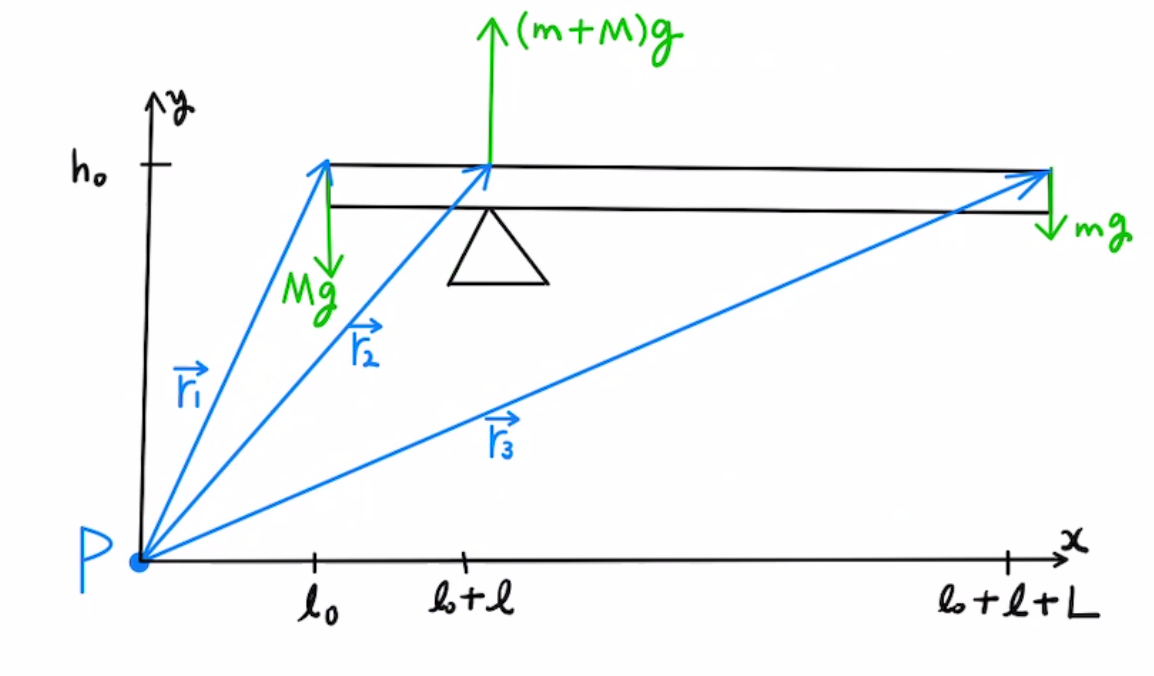
より簡略化した解法
今までの話を踏襲し、平面で考える場合のより簡単な解法を考えます。
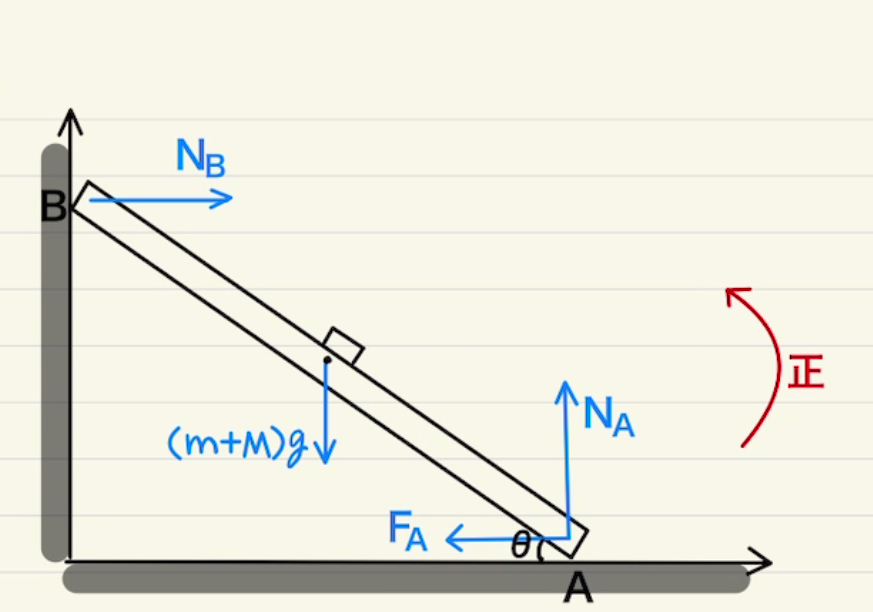
良問の風問11のような壁に物を立てかけておいた棒を想定しましょう。
棒には垂直抗力と摩擦力がかかっています。それらを図に書き込むと下のようになります。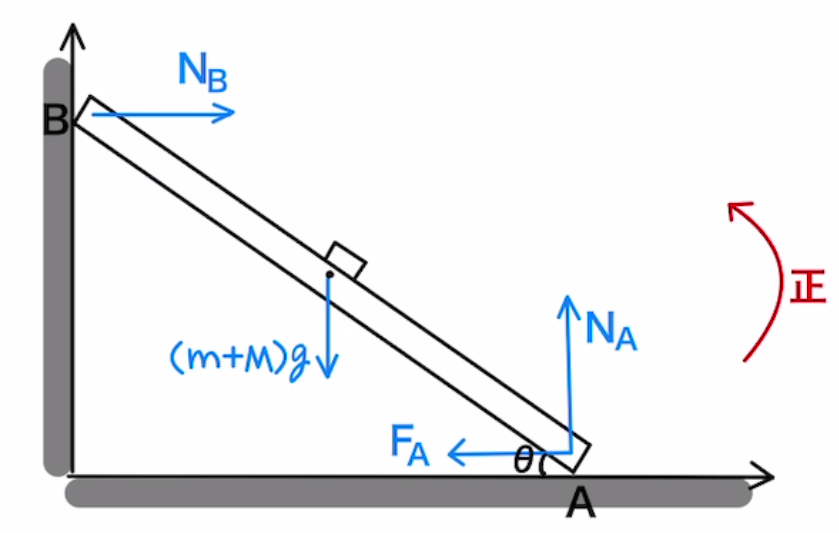
このとき二つのやり方が考えられます。
・ $x$軸 $y$軸に投影する
回転中心$P$を重心に設定します。
そうすることにより、重心のモーメントが$0$となることで計算が楽になります。
図のようにPを原点にして座標を書くと、$x$軸と$y$軸にそれぞれの力が投影できます。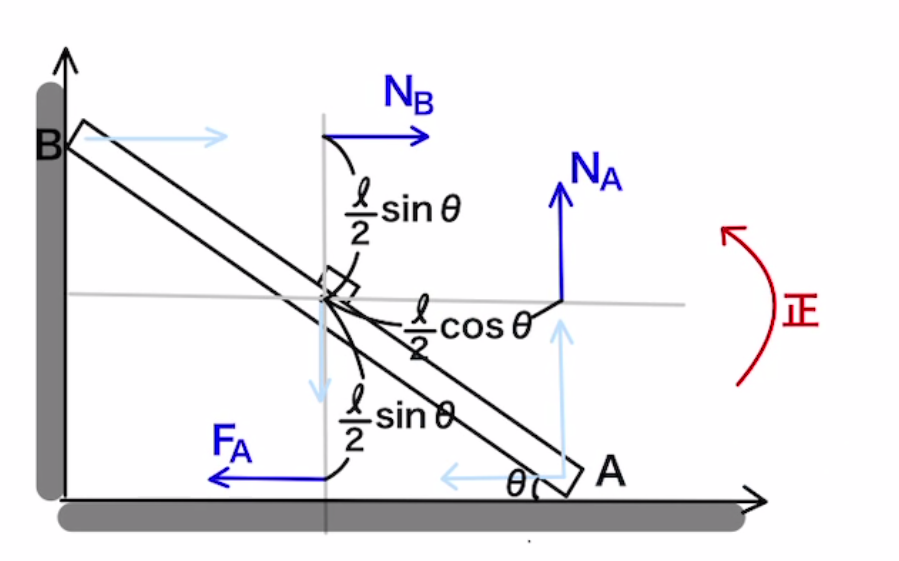
それらの力を左回りと右回りに分類して、その合計が同じになることでモーメントはつり合います。左回りのモーメント=右回りのモーメントとなるので
$$N_A ・ \frac{l}{2}\cos{θ}= F_A ・ \frac{l}{2}\sin{θ} + N_B ・ \frac{l}{2}\sin{θ} $$
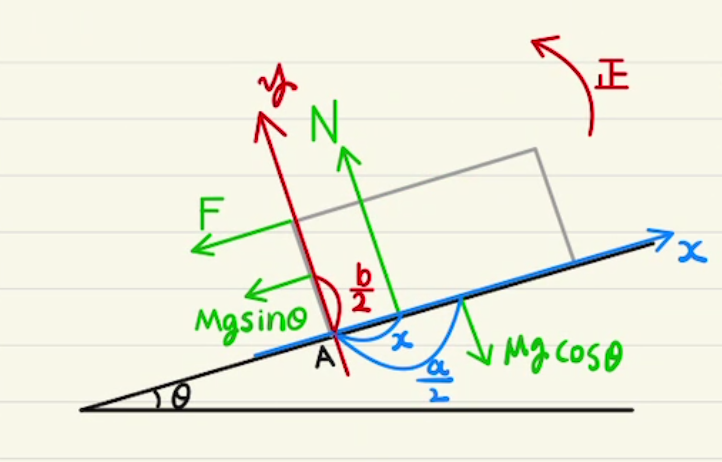
・棒に沿った直線を考え、垂直成分だけを抽出する(棒状の物体のみ)
この方法は棒状(一次元)の剛体にしか適用できませんが、回転方向がわかりやすいです。
今回も回転中心$P$を重心に設定して、$P$以外でかかっている力を棒に垂直な成分だけを抽出します。
左回りのモーメント=右回りのモーメントとなるので
$$N_A \cos{θ} ・ \frac{l}{2}= F_A \sin{θ} ・ \frac{l}{2} + N_B \sin{θ}・\frac{l}{2} $$ 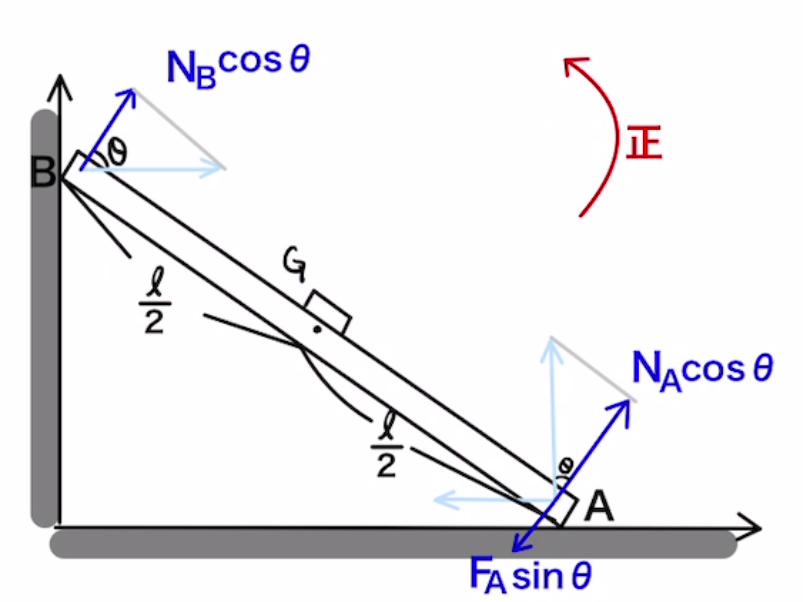
まとめ
モーメントのつり合っているときは任意の点を取り、そこからの位置ベクトル$ \vec{r} $と力ベクトル$ \vec{f} $から
$$\vec{0} = \sum{\vec{r} × \vec{f}} $$
が成り立ちます。
$xy$平面で考える場合は、
$$0 = \sum{(xf_y-yf_x)}$$
となります。
二つのベクトルのなす角度$θ$とすると
$$0 = \sum{ ( |\vec{r}| |\vec{f}| \sin{θ} )}$$
$\sin{θ}$がプラスの時は左回りのモーメント
$\sin{θ}$がマイナスの時は右回りのモーメント
とおけるので、それぞれの絶対値の合計が等しいと考えてもよいでしょう。
このとき$x$軸と$y$軸に力を投影して書き込むとわかりやすくなります。