力学⑥ 単振動

単振動は力学で最も難しい分野であり、入試では頻出の分野でもあります。
微分方程式をつかった話にもなりますので、理解には少し時間がかかるのは覚悟しましょう。

単振動の最も単純なモデルを見ていきます。
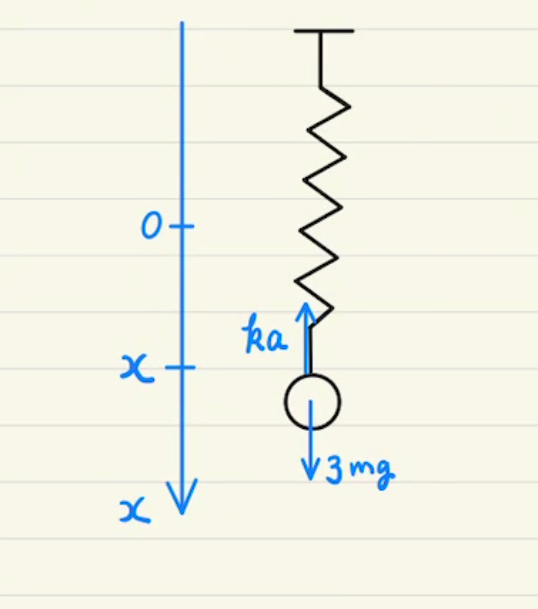
まずばねに取り付けられている物体を考えます。

バネが自然長のときを原点にとります。
バネは伸びているときは$x$負の方向に$kx$の力がかかり、バネが縮んでいるときは $x$正の方向に$-kx$の力がかかる。そのため常に$f=-kx$となります。

ここでは一回時間微分するごとに文字の上に点を一つ書くことにしましょう。
つまり速度$v=\dot{x}$、加速度$a=\ddot{x}$となります。

このとき運動方程式は
$$m\ddot{x} = – kx $$
となります。ここで $\ddot{x}$は$x$の時間微分を二回したもの、つまり加速度です。
これを整理して
$$\ddot{x} = – \frac{k}{m}x $$
位置によって加速度が変わるというかなり複雑な式となってしまいました。
これを微分方程式といいます。
これをちゃんと数学的に解くのは少し大変なので今回は結果から先に書いてしまいます。
$ω=\sqrt{ \frac{k}{m} } $と置くと、
$$x(t) = C_1 \cos{ωt} + C_2\sin{ωt} \tag{①}$$
これが単振動の運動方程式の一般解となります。
$C_1$と$C_2$は積分定数といい、初期位置と初速度で求めていくことになります。
(①)式を微分すると
$$v(t) = -C_1ω \sin{ωt} + C_2ω\cos{ωt} \tag{②} $$
となるため、 (①),(②)式にそれぞれにt=0を代入すると
$$x(0) = C_1 $$
$$v(0) = C_2ω $$
となるため $C_1 = x(0), C_2 = \frac{v(0)}{ω} $となり、
$$x(t) = x(0) \cos{ωt} + \frac{v(0)}{ω}\sin{ωt}　 \tag{①’} $$
$$v(t) = -x(0)ω \sin{ωt} + v(0)\cos{ωt}　 \tag{ ②’ } $$
が単振動の動きとなります。
多くの問題では $x(0)$ か $v(0)$ のどちらかが0となるため、$\cos$か$\sin$のシンプルな形になるが、難問では$\sin$と$\cos$の合成が必要になることもあります。

また、 ①’ ,②’から
$$ (ω x)^2 + v^2 = 一定$$
の特性も知っていると便利です。

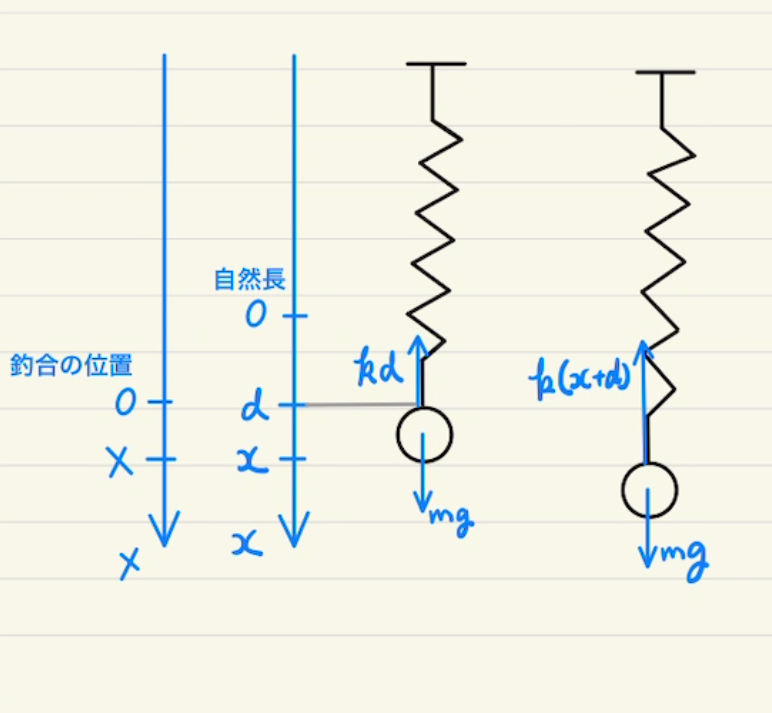
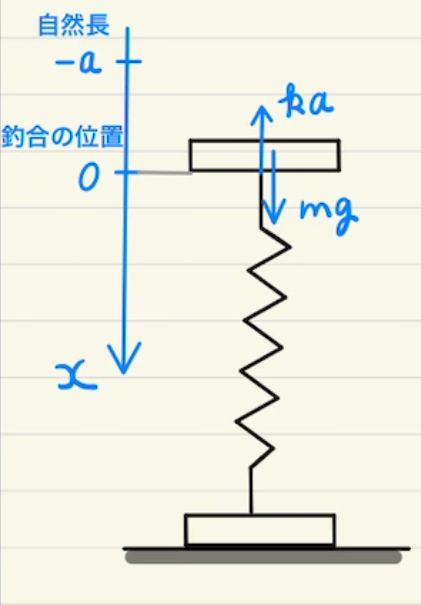
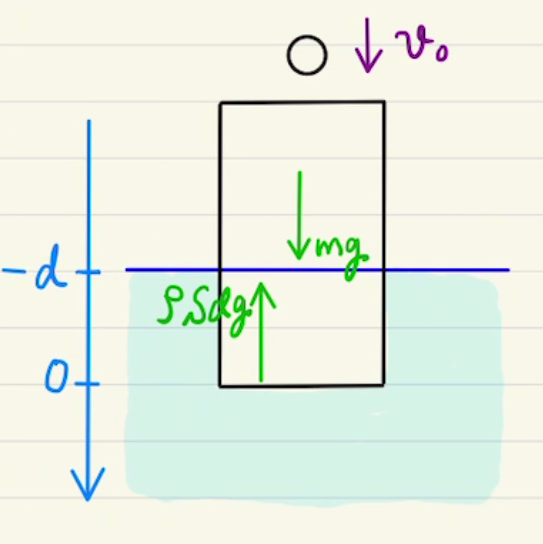
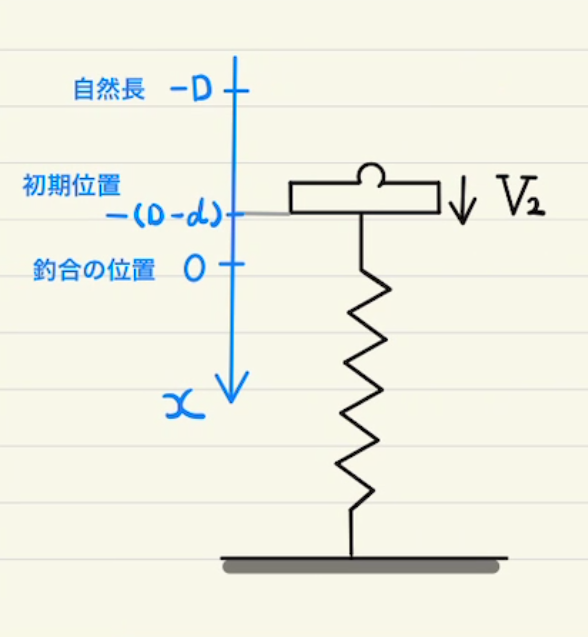
振動中心が原点ではなく$x=d$にある場合は
$$\ddot{x} = – \frac{k}{m}(x – d) $$
で表されます。
このとき $X = (x – d) $ とおくことによって
$$\ddot{X} = – \frac{k}{m}X $$
と書き直すことができます。
これを先ほどのように解くと
$$X(t) = X(0) \cos{ωt} + \frac{v(0)}{ω}\sin{ωt}$$
となり$x(t)$で書き直すと
$$x(t) = (x(0) – d) \cos{ωt} + \frac{v(0)}{ω}\sin{ωt} + d$$

これも同様に、
$$ (ω (x – d))^2 + v^2 = 一定$$
の性質があります