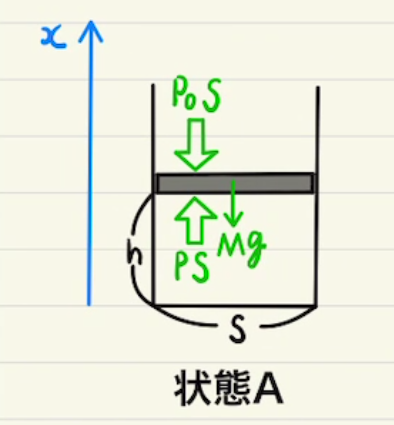
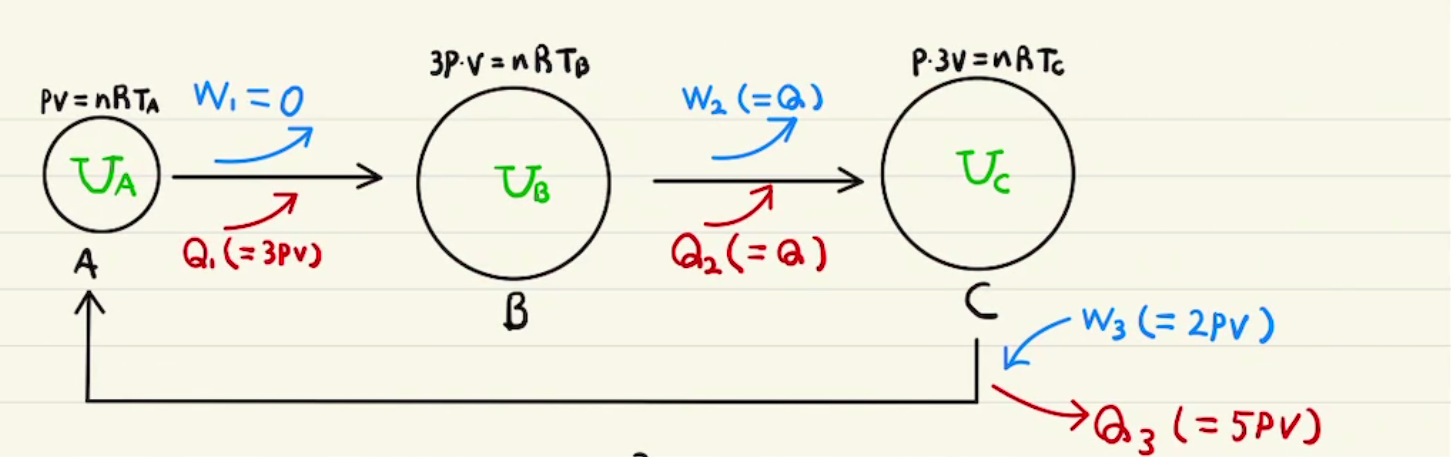
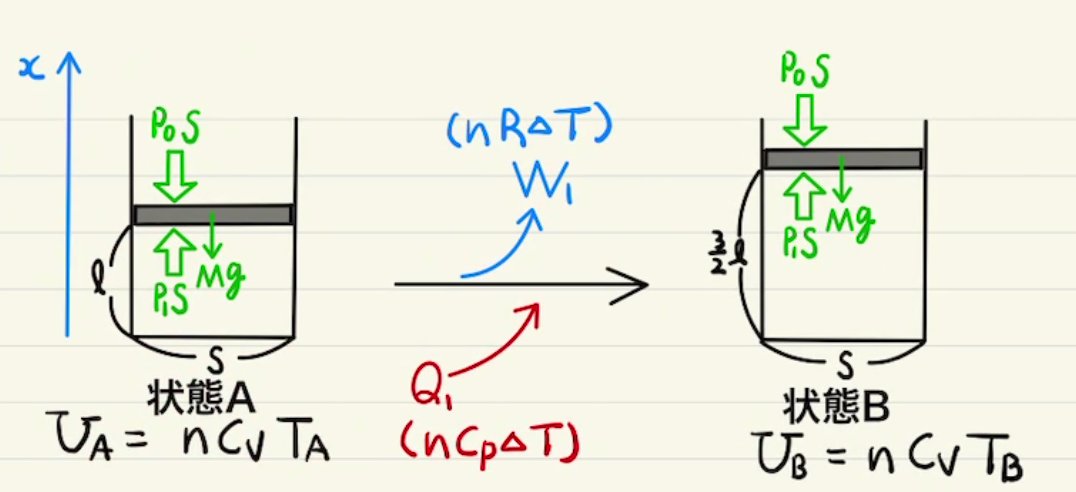
熱力学では主に気体の状態の変化を見ていくことになります。
ではどのようにして気体を変化させるか。
高校物理では二つしかありません。仕事と熱です。
仕事は力学で扱ったように、気体に対して力で押しこむことによって仕事分の気体の内部エネルギーが増えます。逆に気体が物体を押し出せば仕事分のエネルギーが外に逃げていきます。
熱に関してですが、これは単に加熱(温めること)により気体にエネルギーを与えているだけです。逆に冷却してエネルギーを減らすこともできます。
気体の内部エネルギーは気体が外に仕事をすると減り、加熱すると増えます。
式にすると
$$ΔU=-W+Q$$
$ΔU$:気体の内部エネルギーの増加分 $W$:気体が外にする仕事 $Q$:加熱で与えたエネルギー。
と書けます。 これが熱力学第一法則です。
逆に気体が仕事をされれば増えるし、吸熱すればその分減ります。
当たり前すぎる話なので、式を覚える必要は特にありません。
($W$を気体がする仕事とするのか、気体がされる仕事とするのかで正負が逆になりややこしいので、意味だけ理解しましょう。)
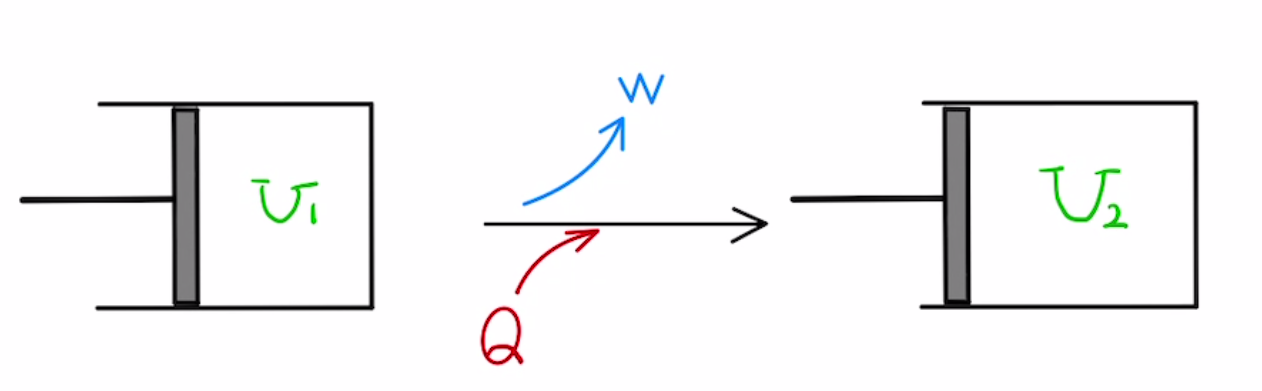
内部エネルギーと仕事
気体の内部エネルギー$U$は気体の分子の運動エネルギーの合計であり
$$U = nC_vT$$
$n$:モル数 $C_v$:定積モル比熱 $T$:絶対温度
で定義されます。
定積モル比熱は分子の種類により定まり、単原子分子では $C_v=\frac{3}{2}R$となります。
良問の風問55のような気体の分子運動によって証明することができます。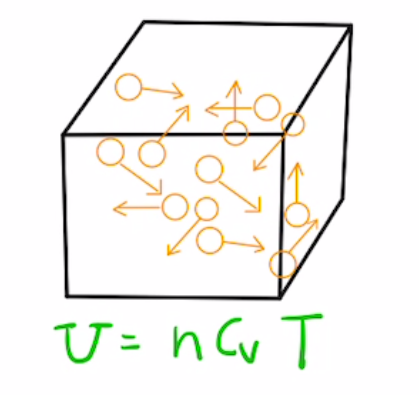
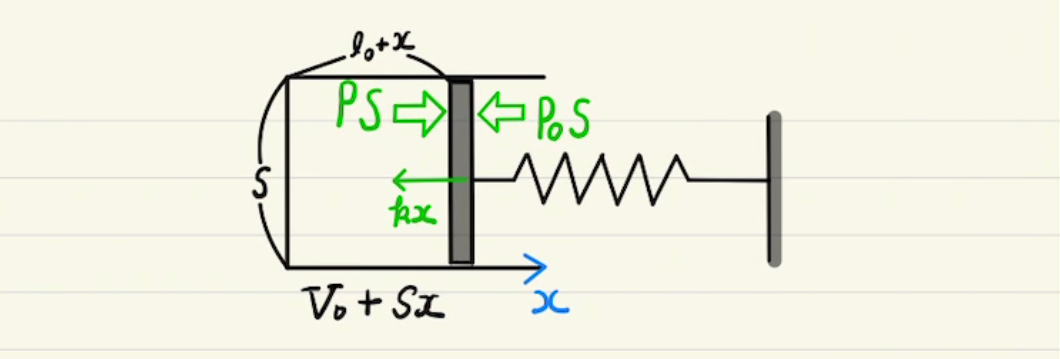
仕事は、気体が外に気体を押し出すと気体が仕事を外にしたことになります。
力学での定義通り$W=\int{fdx}$となります。
これを気体の圧力$P$、気体の体積$V$で書き直したいと思います。
気体が押す部分の面積をSとすると $f=PS$、 $dx=\frac{dV}{S}$ なのでこれを代入すると
$$W=\int{PdV}$$
となります。$W$は$P-V$グラフの面積になると覚えておきましょう。
最後に熱量$Q$を熱力学第一法則から求める形になります。
気体の状態
(理想気体の)気体の状態方程式は以下のように表せます。
$$PV=nRT$$
$P$:気圧[$Pa$] $V$:体積[$m^3$] $T$:温度[$K$]
密閉された容器の場合、変化するのは$P,V,T$であり、これらのうち二つ定まると気体の状態がわかります。
そのため多くの場合、P-Vグラフを書いて状態の変化を見るとわかりやすくなります。
主な状態変化
ここからは4つの状態変化で以下のエネルギー量を見ていきます。
$ΔU$:内部エネルギーの増加量 $W$:外部にした仕事 $Q$:加熱
・等積変化
体積を加熱or吸熱した場合の変化($V$=一定)
動かない容器に密閉したまま加熱したときなどに起こります。
圧力が$ΔP$だけ増えたとき、
$ΔU = nC_vΔT \quad = \frac{C_v}{R} ΔPV$
$W= \int{PdV} = 0$
$Q= \frac{C_v}{R} ΔPV$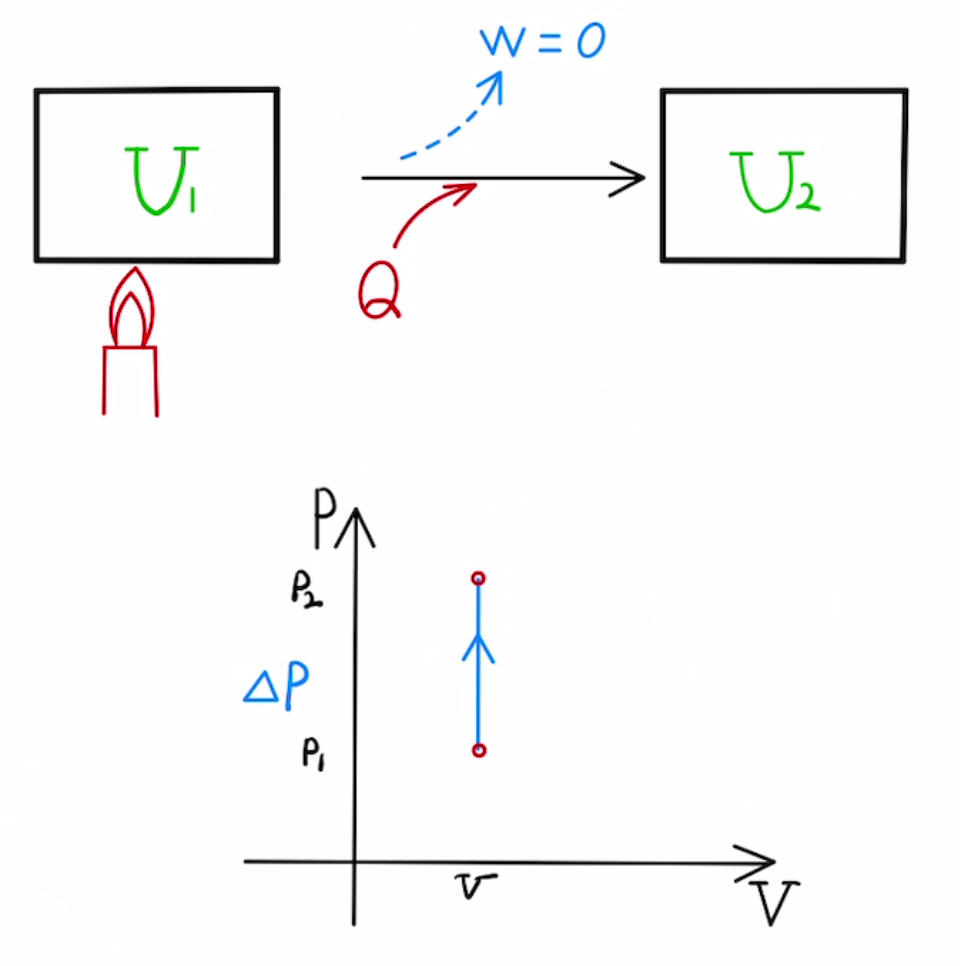
・等圧変化
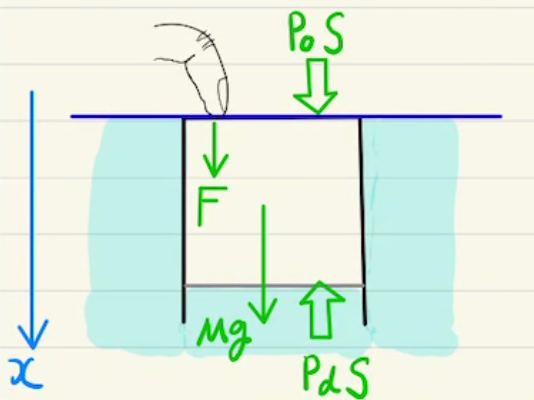
一定の圧力で 加熱or吸熱 させる変化($P$=一定)
ふたを自由に動くようにして加熱したときなどに起こります。
体積が$ΔV$増えたとき 、
$ΔU = nC_vΔT \quad = \frac{C_v}{R}PΔV $
$W = \int{PdV} =PΔV $
$Q= (\frac{C_v}{R}+1)PΔV $
このとき吸熱量が$Q=n(C_v+R)ΔT$ となることから定圧モル比熱$C_p=C_v+R$と定義される。単原子分子なら $\frac{5}{2}R $ となり、 $ΔU:W:Q=3:2:5$となります。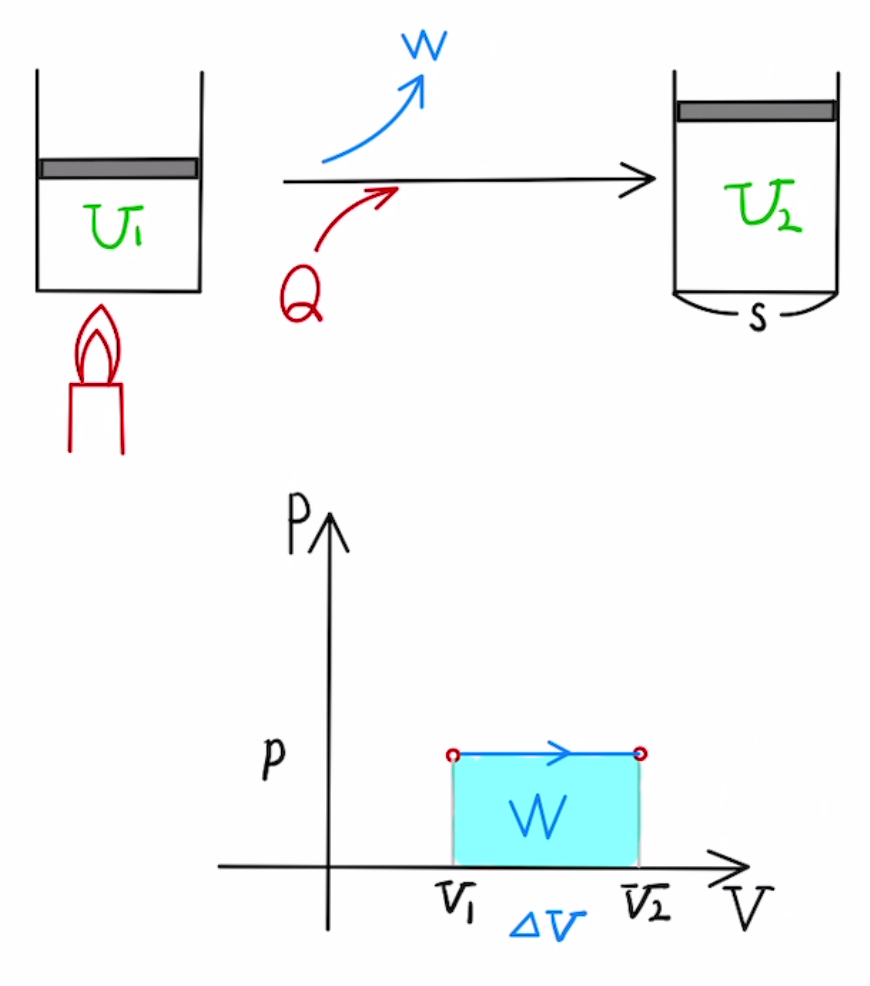
・等温変化
一定の温度で加熱or吸熱させる変化($T$=一定)
水などの中でゆっくりと蓋を動かしたときなどに起こります。
体積の対数が$ Δ(\log{V}) $だけ増加したとき、
$ΔU = nC_vΔT \quad = 0 $
$W = \int{PdV} = nRTΔ(\log{V})$
$Q = W$
これを対数の問題として出題されることはないため、$W$は特に覚えておく必要はないでしょう。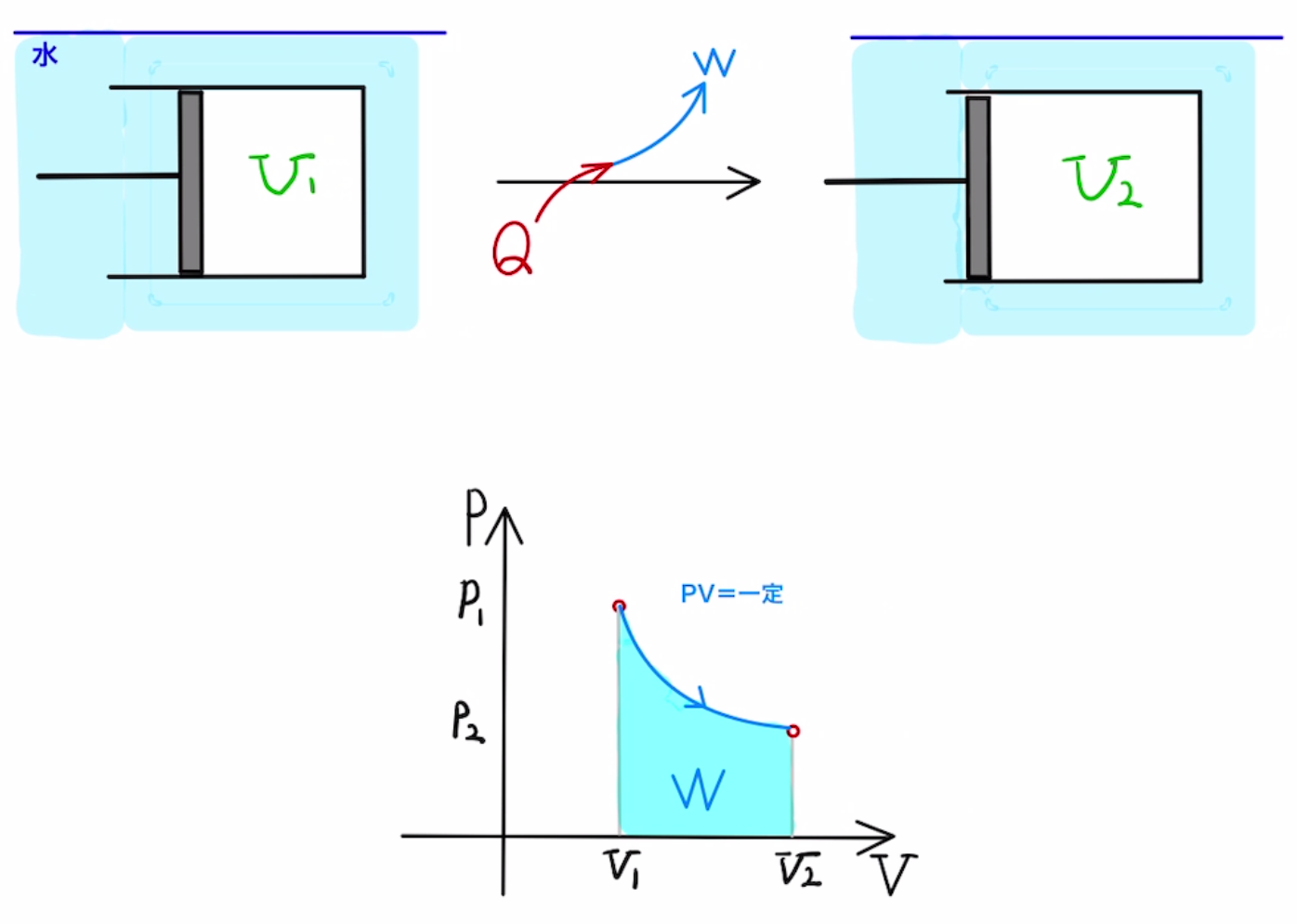
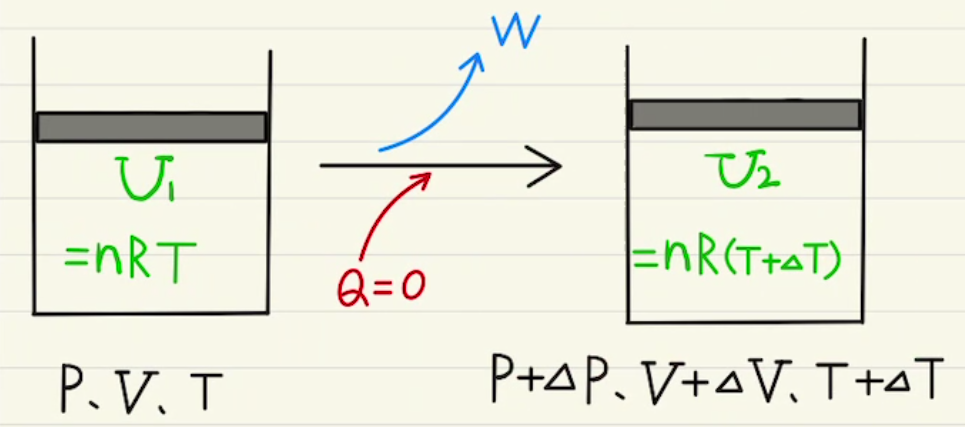
・断熱変化
外部からの熱のやり取りを遮断してさせる変化($Q$=0)
断熱材で囲ったり、外部と熱のやり取りをする間がないくらい早く状態変化させると起こります。ちなみに隕石の先端が高熱になるのは空気の断熱圧縮が起こっているからです。
温度$T$が$ΔT$だけ増加したとき、
$ΔU = nC_vΔT $
$W = ΔU $
$Q = 0$
また断熱変化では以下の式が成り立つ(ポワソンの定理)
$$PV^γ=一定\qquad(γ=\frac{C_p}{C_v})$$
証明は名問の森Ⅰ 57の補足で説明しています。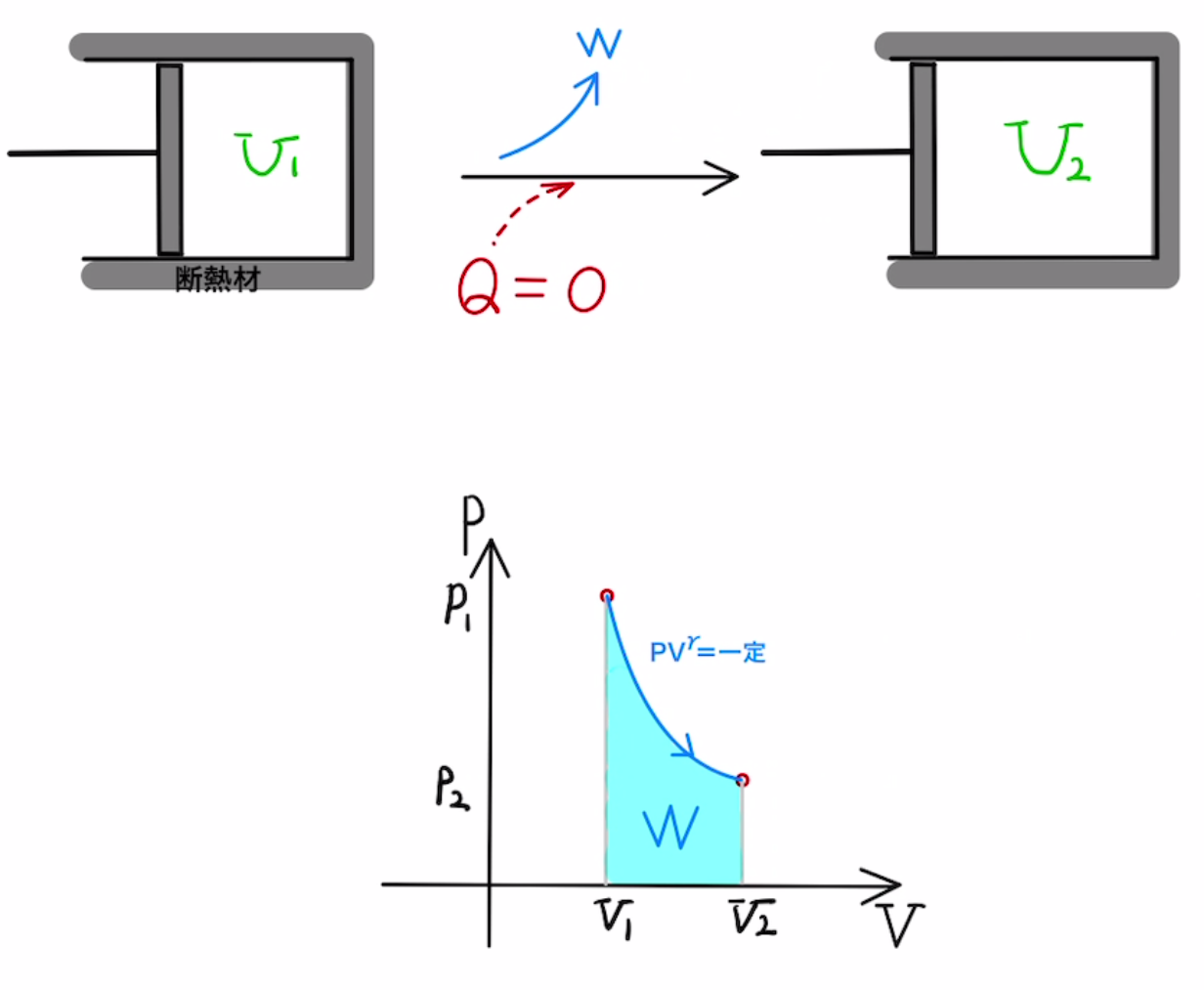
熱サイクル
複数の状態変化を組み合わせて最初の状態まで戻す一連の動きを熱サイクルと言います。
図のP-Vグラフは等温変化と断熱変化を組み合わせてできたサイクルでカルノーサイクルと呼ばれます。このサイクルで燃料を燃やして車の車輪を回転させるエンジンを考えます。
これをひとつずつ見ていきます。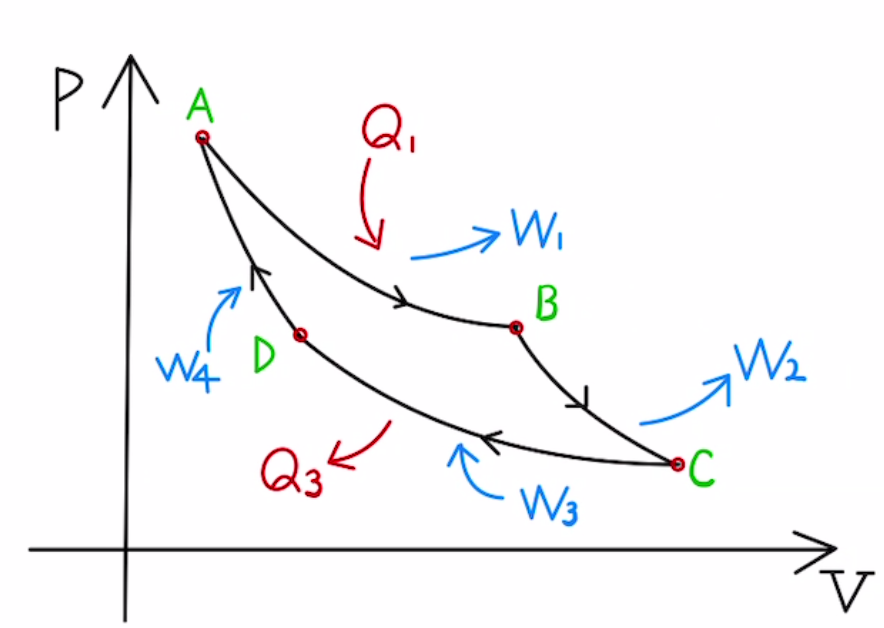
A→Bが等温変化で、燃料を燃やして$Q_1$の熱を与えて仕事$W_1$を取り出して車輪を回転させます。
B→Cは断熱変化で熱のやりとりなく $Q_2=0$で、仕事$W_2$を車輪をさらに回転させます。
C→Dが等温変化で、燃料を燃やして$Q_3$の熱を廃熱し、仕事$W_3$を車輪から奪います。
D→Aは 断熱変化で熱のやりとりなく $Q_4=0$で、仕事$W_4$を車輪から奪います。
・仕事W
ここでまず仕事だけに注目します。
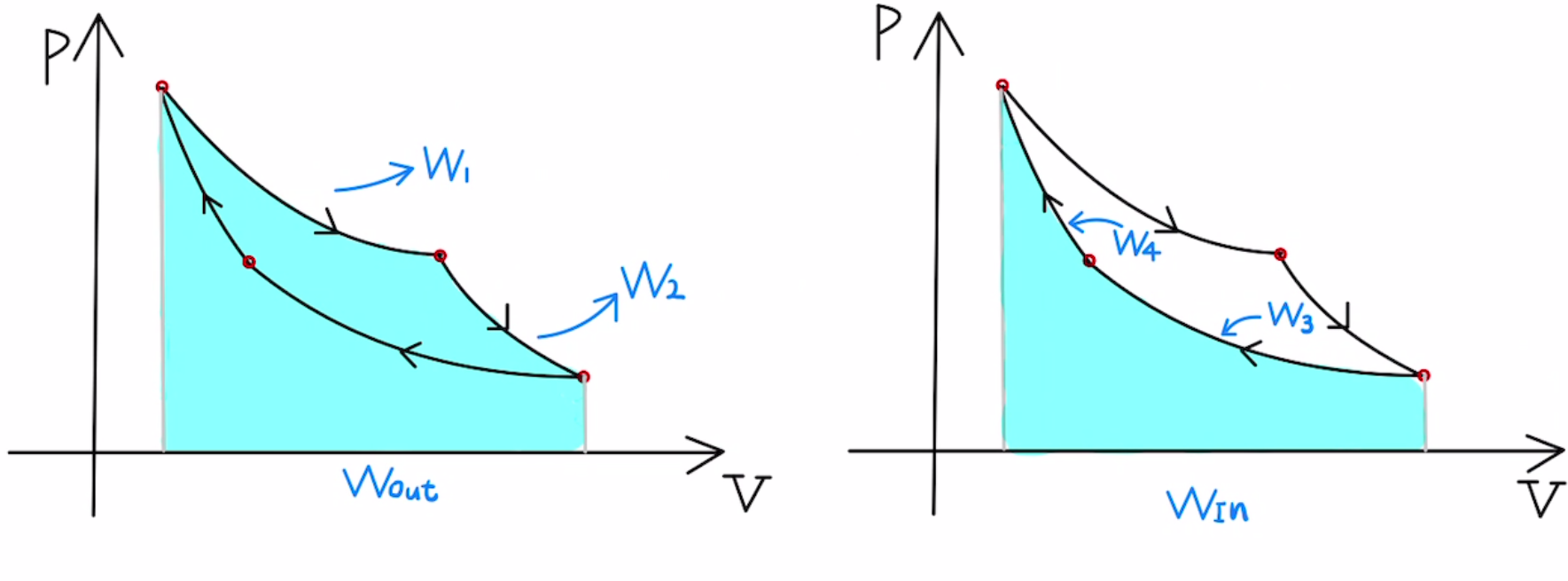
気体が車輪に対してした仕事の合計は$W_{Out}=W_1+W_2$となり
車輪が気体に対してした仕事の合計は$W_{In}=W_3+W_4$となります。
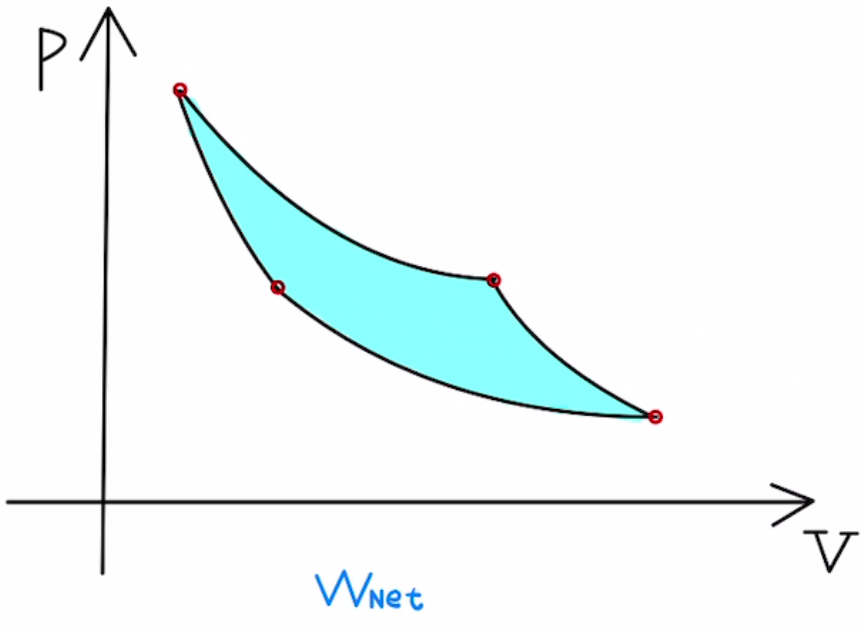
実質的に気体が車輪にした仕事は、$W_{Net}= W_{Out} – W_{In}$となります。
これを正味の仕事と言います。
・熱Q
次に与えた熱について
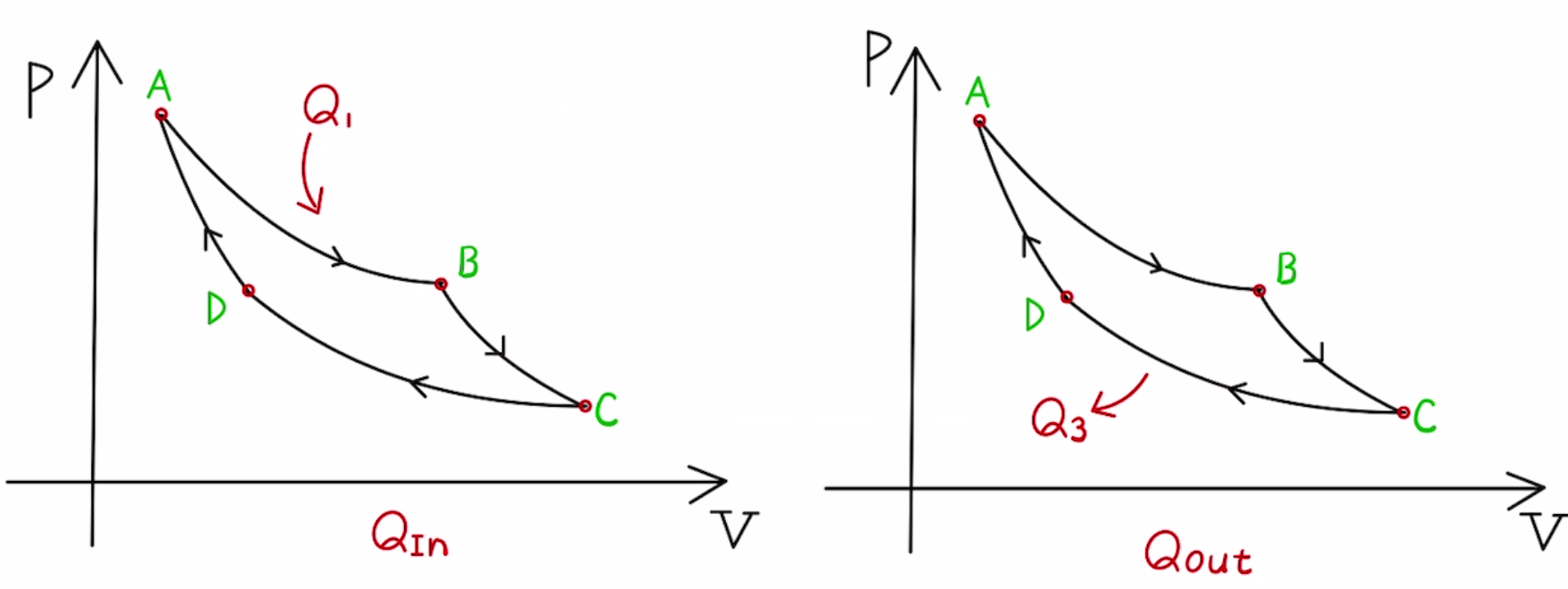
燃料によってエンジンには$Q_{In}=Q_1$の熱エネルギーが与えられ
エンジンからは$Q_{Out}=Q_3$の熱エネルギーが廃熱されます。
廃熱された熱を使うことはできないので、加えた熱エネルギー$Q_{In}$だけを考慮します。
このことから、加えた熱エネルギーからどれだけの(実質的な)仕事を行えるかの効率$e$は次のように定義できます。
$$e=\frac{ W_{Net} }{ Q_{In} }$$
まとめ
・気体のエネルギー $U=nC_vT$は外部にした仕事$W=\int{PdV}$分だけエネルギーを失い、加熱した$Q$分だけエネルギーが増える。
・状態の変化はP-Vグラフにしてみるとわかりやすい。
・各状態では$PV=nRT$が常に成り立つ。
・熱サイクルの効率$e$は以下で定義される。
$$e=\frac{ W_{Out} – W_{In} }{ Q_{In} }$$