(1)(2)は定義に従った電気容量の問題となっています。
コンデンサーの電気容量は
$$C=ε\frac{S}{d}$$
$ε$:誘電率,$S$:極板の面積:,$d$:極板同士の距離
と定義されます。
誘電率は真空の時は $ε_0$と表されますが、これを基準に何倍の誘電率になるかを比誘電率$ε_r$と言います。
つまり、誘電率$ ε= ε_r ε_0 $となります。
このことから
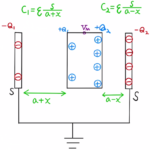
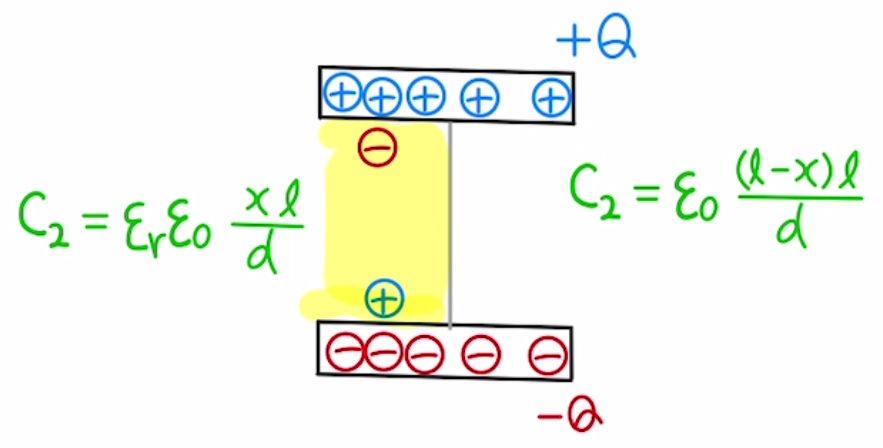
(1)図の黄色の部分の電気容量は
$$C_1= ε_r ε_0 \frac{xl}{d}$$
(2)残りの部分の電気容量は
$$C_2= ε_0 \frac{(l-x)l}{d}$$
となります。
(3)これらが二つ並列されているため、電気容量の合計は
$$C= C_1+C_2 = ε_0 \frac{[l+( ε_r – 1)x]l}{d}$$
(4)よって電荷Qだけたまっているときのエネルギー量は
$$U=\frac{1}{2}\frac{Q^2}{C}= \frac{dQ^2}{2 ε_0 [l+( ε_r – 1)x]l } $$
となります。
(5)この式から$x$増加することで$U$が減少することがわかります。($\frac{dU}{dx}<0$)
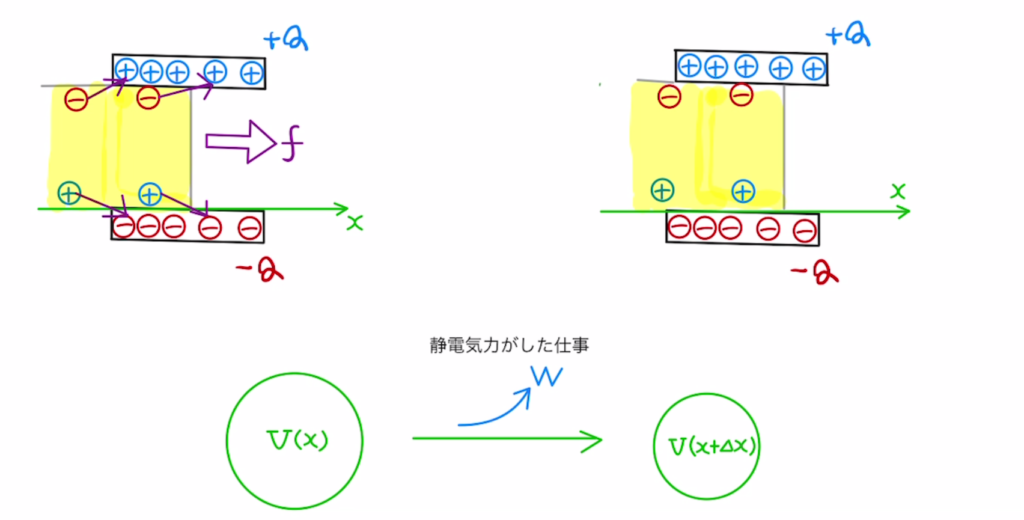
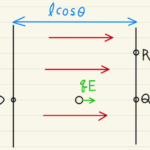
(6)図のように誘電体には電荷の偏りがあるので、それによって右方向に静電気力が働くことが確認できます。
これは静電エネルギーによっても説明できます。
静電気力$f$が誘電体を動かしたときに(静電気が)仕事をしたことになります。
このした仕事は$W=\int{fdx}$(仕事は力の積分)と定義されるため、逆に$f=\frac{dW}{dx}$(力は仕事の微分)と書き換えることもできます。
今、静電気が仕事をした分は静電エネルギーが減少し運動エネルギーに変換されるため$W=-ΔU$となります。
ここから
$$f=\frac{dW}{dx}=-\frac{d(ΔU)}{dx} =-\frac{dU}{dx}>0$$
となり、$x$正の方向、つまり右に力がかかることが確認できます。
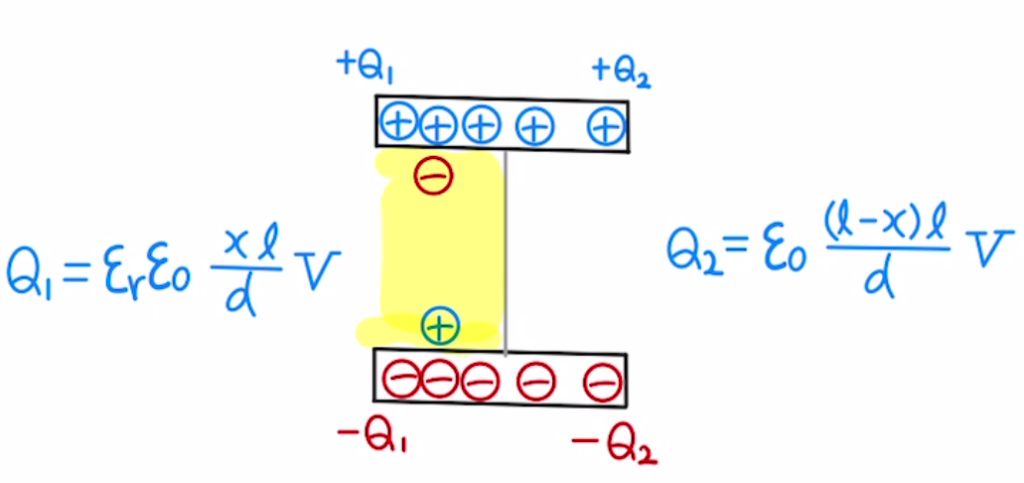
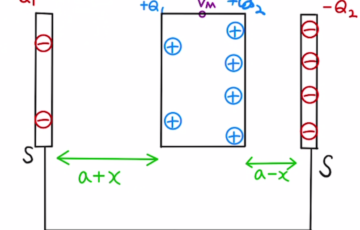
(7)それぞれの電気量は
$$Q_1= C_1V= ε_r ε_0 \frac{xl}{d}V $$
$$Q_2= C_2V= ε_0 \frac{(l-x)l}{d}V $$
であることから、面積当たりの電気量は
$$\frac{Q_1}{lx}: \frac{Q_2}{l(l-x)} = ε_r:1 $$
これは面積と幅が等しいときの電気容量は真空の時より誘電体のほうが$ ε_r $倍になるという定義と一致しますね。